Содержание
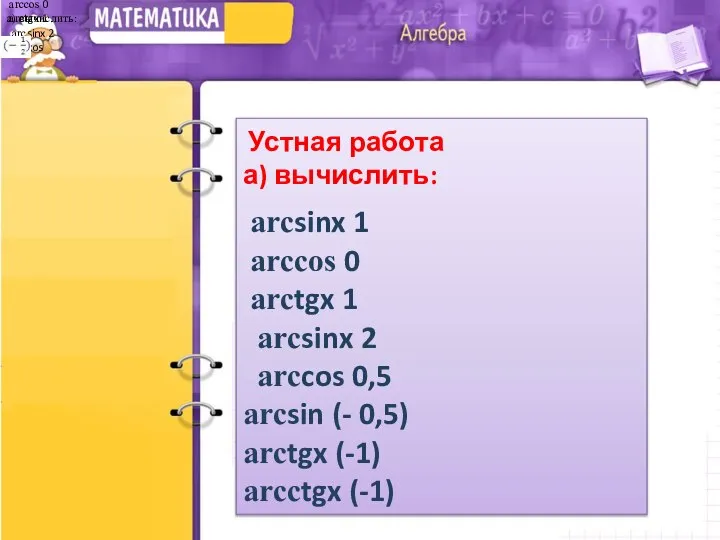
- 2. arcsinx 1 arccos 0 arctgx 1 arcsinx 2 arccos Устная работа а) вычислить: arcsinx 1 arccos
- 3. arcsinx 1 arccos 0 arctgx 1 arcsinx 2 arccos Устная работа б) вычислить: arcsinx 1 +
- 4. «Верно - неверно». 1) sin2x+cos2x=1 – основное тригонометрическое тождество? 2) sinx, cosx, tgx, ctgx – тригонометрические
- 5. «Верно - неверно». 9) arctg(-2) – имеет смысл? 10) R - область значения функции tgx. 11)
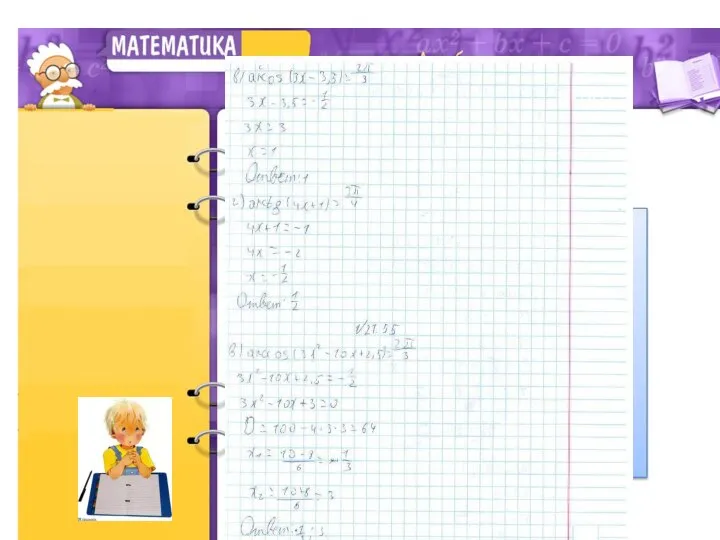
- 6. Проверка домашнего задания № 21.55 в) arccos(3х2 – 10х +2,5) = 2П/3 г) arcсtg (х3- 8х2+15х+
- 7. Проверка домашнего задания № 21.55 в) arccos(3х2 – 10х +2,5) = 2П/3 г) arcсtg (х3- 8х2+15х+
- 8. Проверка домашнего задания № 21.55 в) arccos(3х2 – 10х +2,5) = 2П/3
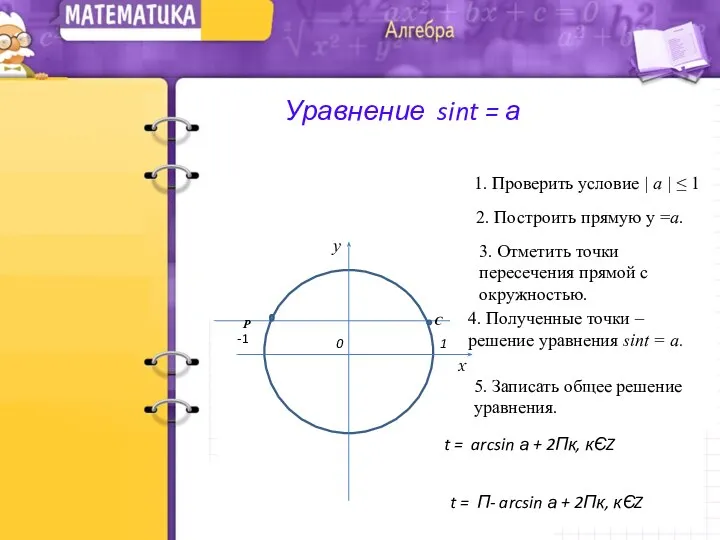
- 9. 1. Проверить условие | a | ≤ 1 y 0 -1 1 x М N 2.
- 10. 1. Проверить условие | a | ≤ 1 y 0 -1 1 x С Р 2.
- 12. Скачать презентацию






 Моменты случайной величины
Моменты случайной величины Пифагор. Пифагорейская школа
Пифагор. Пифагорейская школа Презентация на тему УМНОЖЕНИЕ ДРОБЕЙ
Презентация на тему УМНОЖЕНИЕ ДРОБЕЙ  Окружность Аполлония
Окружность Аполлония Математика. Урок 4
Математика. Урок 4 Презентация на тему Конкретный смысл деления
Презентация на тему Конкретный смысл деления  Понятие предела функции
Понятие предела функции Вычитание числа 7
Вычитание числа 7 Решение заданий с параметром. Занятие №1
Решение заданий с параметром. Занятие №1 Эки эселенген бурчтун тригонометриялык функциялары
Эки эселенген бурчтун тригонометриялык функциялары Роль и место математики в современном мире. Пределы, их свойства (лекция 1)
Роль и место математики в современном мире. Пределы, их свойства (лекция 1) Производная функции
Производная функции Случаи вычитания 11-
Случаи вычитания 11- Число и цифра 0. Сложение и вычитание с числом 0
Число и цифра 0. Сложение и вычитание с числом 0 Првильные многоугольники
Првильные многоугольники Стороны треугольника пропорциональны синусам противолежащих углов
Стороны треугольника пропорциональны синусам противолежащих углов Интегрированный урок в 7 классе Грамотная геометрия - геометрия + русский язык
Интегрированный урок в 7 классе Грамотная геометрия - геометрия + русский язык Funksiya. Funksiyaning berilish usullari
Funksiya. Funksiyaning berilish usullari Презентация на тему УСТНЫЕ ЗАДАЧИ НА ПРИМЕНЕНИЕ АКСИОМ СТЕРЕОМЕТРИИ
Презентация на тему УСТНЫЕ ЗАДАЧИ НА ПРИМЕНЕНИЕ АКСИОМ СТЕРЕОМЕТРИИ  Скалярное произведение векторов. Угол между векторами
Скалярное произведение векторов. Угол между векторами Complete each of the following:
Complete each of the following: Задача на знаходження суми
Задача на знаходження суми Решаем задачи на логику. Занятие 5
Решаем задачи на логику. Занятие 5 Презентация на тему Параллелограмм. Свойства параллелограмма
Презентация на тему Параллелограмм. Свойства параллелограмма  Математическая викторина
Математическая викторина Модель пирамиды
Модель пирамиды Презентация на тему Сочетательное свойство сложения
Презентация на тему Сочетательное свойство сложения  Презентация на тему Подготовка к ЕГЭ по математике
Презентация на тему Подготовка к ЕГЭ по математике