Содержание
- 2. www.themegallery.com Бер Л.М. Обыкновенные диференциальные уравнения ГОУ ВПО НИ ТПУ Рег. № 189 от 17.06.10 Алгоритм
- 3. www.themegallery.com Бер Л.М. Обыкновенные диференциальные уравнения ГОУ ВПО НИ ТПУ Рег. № 189 от 17.06.10
- 4. www.themegallery.com Бер Л.М. Обыкновенные диференциальные уравнения ГОУ ВПО НИ ТПУ Рег. № 189 от 17.06.10 ЛНДУ
- 5. www.themegallery.com Бер Л.М. Обыкновенные диференциальные уравнения ГОУ ВПО НИ ТПУ Рег. № 189 от 17.06.10 ЛНДУ
- 6. www.themegallery.com Бер Л.М. Обыкновенные диференциальные уравнения ГОУ ВПО НИ ТПУ Рег. № 189 от 17.06.10 ЛНДУ
- 7. www.themegallery.com Бер Л.М. Обыкновенные диференциальные уравнения ГОУ ВПО НИ ТПУ Рег. № 189 от 17.06.10 Форма
- 8. www.themegallery.com Бер Л.М. Обыкновенные диференциальные уравнения ГОУ ВПО НИ ТПУ Рег. № 189 от 17.06.10 ЛНДУ
- 9. www.themegallery.com Бер Л.М. Обыкновенные диференциальные уравнения ГОУ ВПО НИ ТПУ Рег. № 189 от 17.06.10 Метод
- 10. www.themegallery.com Бер Л.М. Обыкновенные диференциальные уравнения ГОУ ВПО НИ ТПУ Рег. № 189 от 17.06.10 Алгоритм
- 12. Скачать презентацию

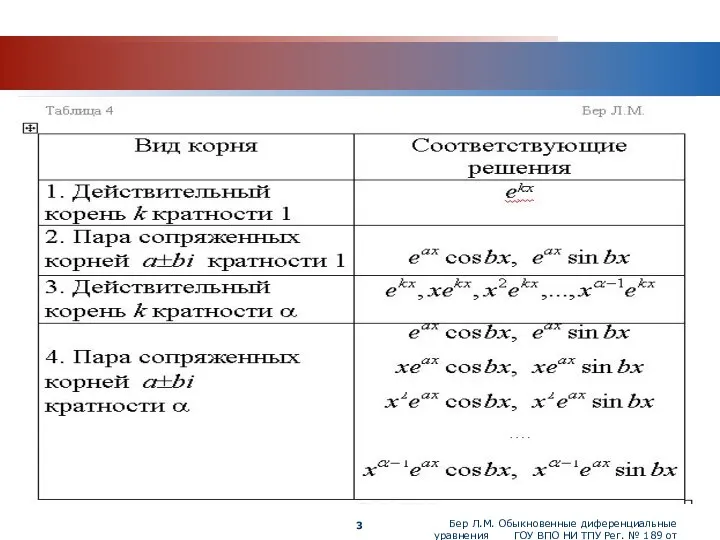







 Навыки решения составных задач
Навыки решения составных задач Введение в стереометрию. Аксиомы стереометрии и некоторые следствия из аксиом. 10 класс
Введение в стереометрию. Аксиомы стереометрии и некоторые следствия из аксиом. 10 класс Виды графов. Тема 4.2
Виды графов. Тема 4.2 Вычисление площадей с помощью интегралов
Вычисление площадей с помощью интегралов Параллельные прямые
Параллельные прямые Презентация на тему Связь между слагаемыми и суммой
Презентация на тему Связь между слагаемыми и суммой  Логарифмы вокруг нас
Логарифмы вокруг нас Основное тригонометрическое тождество и его следствия
Основное тригонометрическое тождество и его следствия Кривая производственных возможностей
Кривая производственных возможностей ЦАРСКОЙ ДОРОГИ В МАТЕМАТИКЕ НЕТ.
ЦАРСКОЙ ДОРОГИ В МАТЕМАТИКЕ НЕТ. Умножение десятичных дробей. Графический диктант
Умножение десятичных дробей. Графический диктант Многоугольники в нашей жизни
Многоугольники в нашей жизни Математическая игра История школы в цифрах
Математическая игра История школы в цифрах Геометрическая прогрессия
Геометрическая прогрессия Описательная статистика
Описательная статистика Теория вероятностей
Теория вероятностей Математика вокруг нас
Математика вокруг нас Презентация на тему Задачи по теме треугольники
Презентация на тему Задачи по теме треугольники  Иррациональные уравнения. 8 класс
Иррациональные уравнения. 8 класс Презентация на тему Равнобедренный треугольник, признаки равенства треугольников
Презентация на тему Равнобедренный треугольник, признаки равенства треугольников  Арифметическая игра. Чебурашка и числовые домики
Арифметическая игра. Чебурашка и числовые домики Путешествие в историю чисел
Путешествие в историю чисел Квадратичная функция и её график
Квадратичная функция и её график Статистическая теория радиотехнических систем. Вероятностные характеристики огибающей и фазы узкополосногонормального процесса
Статистическая теория радиотехнических систем. Вероятностные характеристики огибающей и фазы узкополосногонормального процесса Симметрия
Симметрия История возникновения числа ПИ
История возникновения числа ПИ Умножение дробей
Умножение дробей 15 минут о математике
15 минут о математике