Слайд 2Эпіграф да ўрока:
Математику уже затем надо учить, что она ум в порядок

приводит.
М. В. Ломоносов
Слайд 3Звернемся да
наступнай
задачы

Слайд 4
Задача. У двух вагонах электрычкі 120 пасажыраў. Калі з першага вагона

ў другі перасядуць 15 чалавек, то ў другім вагоне пасажыраў стане ў 2 разы больш, чым было ў першым вагоне спачатку. Колькі пасажыраў было ў першым вагоне да перасадкі?
Няхай х – лік пасажыраў 1 вагона да перасадкі, тады пасля перасадкі іх застанецца (х – 15) чалавек, а ў другім вагоне стане (2х) чалавек. Разам іх 120 пасажыраў, значыць х – 15 + 2х = 120.
Атрыманая роўнасць са зменнай называецца ўраўненнем. Рэшым яго. 3х = 120 +15, 3х = 135, х = 45. Лік 45 называецца коранем ўраўнення.
Слайд 5
Мэты урока:
фарміраваць паняцці «ўраўненне з адной зменнай», «корань ураўнення»;
замацоўваць уменні рашэння ўраўненняў;
развіваць

мысленне, памяць, уважлівасць.
Слайд 6Ураўненнем называецца роўнасць са зменнай.
Коранем ураўнення называецца значэнне зменнай, пры якім ураўненне

ператвараецца ў правільную лікавую роўнасць.
Рашыць ураўненне – значыць знайсці ўсе яго карані або даказаць, што іх няма.
Слайд 7
Прыклады ўраўненняў:
1) 7х = 42;
2) -6 х – 12 = 0;
3) 5х

+ 2(х – 1) = 12;
4) 3,5х – 7(0,5х + 1) = 9;
Слайд 8Ураўненне выгляду
ax = b, дзе a і b – лікі,
а

х – зменная, называецца лінейным.
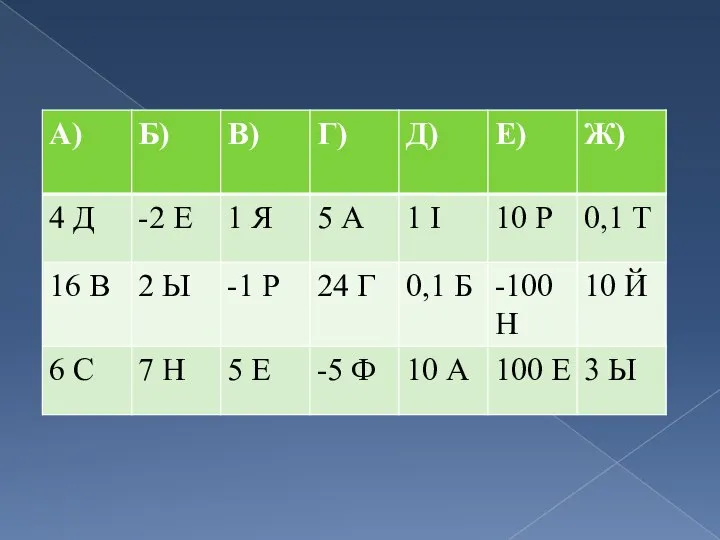
Слайд 9Назавіце лікі a і b ва ўраўненнях:
3х = 15, -6х = 48,

-9х = -9,
0х = 20, 3х = 0.
Слайд 11Рэшым некалькі ўраўненняў:
1) 5 · х = 4,5; 2) 0 ·х =

- 25;
3) 0 · х = 10; 4) – 6х = 0;
5) 0 · х = 0; 6) 12 х = - 48;
Слайд 12Лінейнае ўраўненне з адной зменнай ax = b можа:
1) мець адзіны корань;
2)

не мець каранёў;
3) мець бясконца многа каранёў.
Слайд 15Гэтае слова:
Дыяфант Александрыйскі, старажытнагрэчаскі матэматык, які жыў у трэцім стагоддзі нашай эры,

заснавальнік алгебры.
Слайд 20Ацаніце свой настрой пасля ўрока.


















 Переменная величина
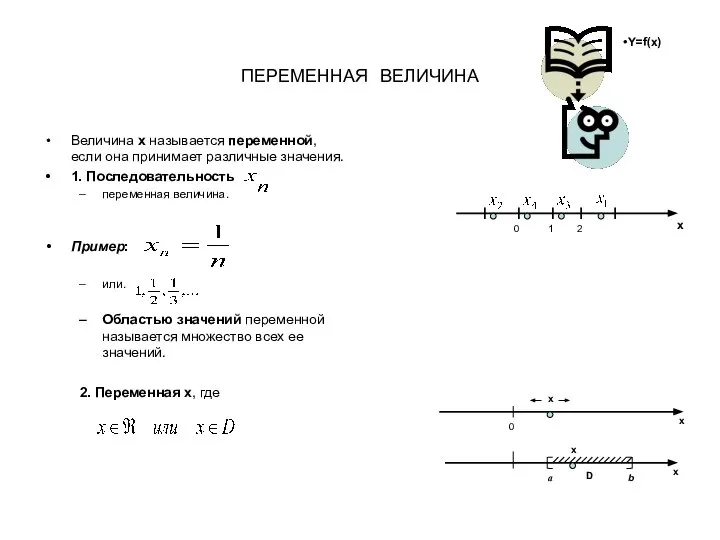
Переменная величина Квадратный корень
Квадратный корень Соответствия величин вычисления. 11 класс, 9 задание
Соответствия величин вычисления. 11 класс, 9 задание Сложение и умножение вероятностей. Полная вероятность. Формула Бейеса. Лекция 2
Сложение и умножение вероятностей. Полная вероятность. Формула Бейеса. Лекция 2 Арккосинус. Решение уравнения cos t = a
Арккосинус. Решение уравнения cos t = a Презентация на тему Единицы массы. Тонна. Центнер (4 класс)
Презентация на тему Единицы массы. Тонна. Центнер (4 класс)  Л 5 Функция одной переменной
Л 5 Функция одной переменной Понятие ”тетраэдр”
Понятие ”тетраэдр” Графы и их применение при решении задач
Графы и их применение при решении задач Аксиомы стереометрии
Аксиомы стереометрии Теория графов. Основные понятия
Теория графов. Основные понятия Сложение вида +2 +3 с переходом через десяток
Сложение вида +2 +3 с переходом через десяток Линейные неравенства с параметром
Линейные неравенства с параметром Решение задач
Решение задач Визуализация операций над эллиптическими кривыми
Визуализация операций над эллиптическими кривыми Область определения функции
Область определения функции Свойства алгоритма
Свойства алгоритма Движение по окружности
Движение по окружности Логарифмические уравнения и неравенства
Логарифмические уравнения и неравенства Типы задач на проценты
Типы задач на проценты Презентация на тему Деление многозначных чисел
Презентация на тему Деление многозначных чисел  Измеряй и сравнивай
Измеряй и сравнивай Тела вращения. Открытый урок
Тела вращения. Открытый урок Формулы для радиусов вписанной и описанной окружностей треугольника
Формулы для радиусов вписанной и описанной окружностей треугольника 3.3. Понятие функции
3.3. Понятие функции Как помочь ребенку понять математику. Вебинар 2
Как помочь ребенку понять математику. Вебинар 2 Уточнение параметров в ксеноновых процессах в реакторах типа ВВЭР-1000 при помощи экспериментальных данных
Уточнение параметров в ксеноновых процессах в реакторах типа ВВЭР-1000 при помощи экспериментальных данных Theorem of rational root with integral coefficients
Theorem of rational root with integral coefficients