Содержание
- 2. Иерархия операций алгебры логики Принцип суперпозиции позволяет использовать простые операции для построения других, более сложных функций.
- 3. Свойства операций алгебры логики Свойства операции отрицание a) Закон двойного отрицания: b) Следствие: знак отрицания, стоящий
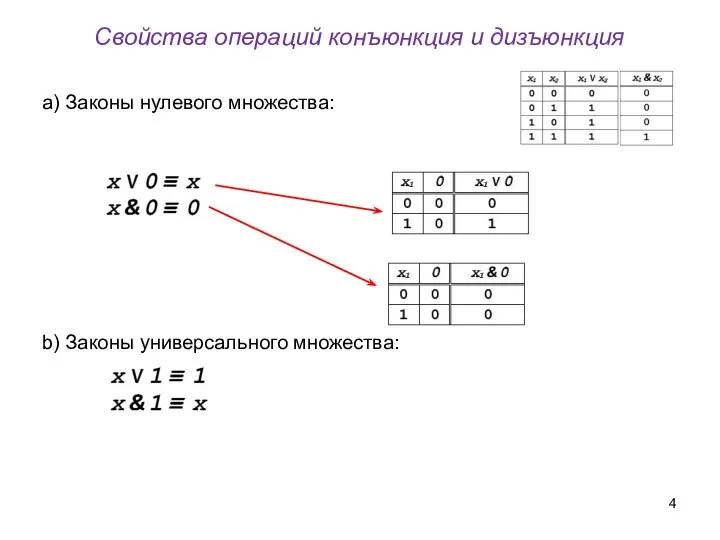
- 4. Свойства операций конъюнкция и дизъюнкция a) Законы нулевого множества: b) Законы универсального множества:
- 5. c) Законы идемпотентности: d) Закон исключенного третьего: e) Закон логического противоречия: Свойства операций конъюнкция и дизъюнкция
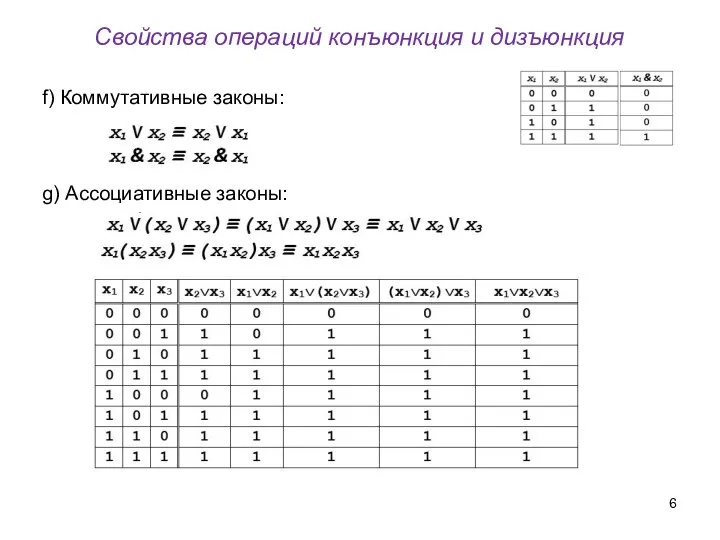
- 6. Свойства операций конъюнкция и дизъюнкция f) Коммутативные законы: g) Ассоциативные законы:
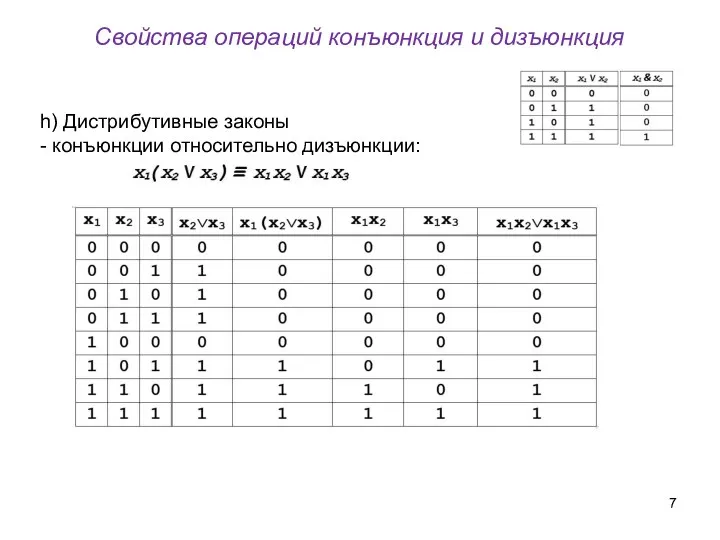
- 7. Свойства операций конъюнкция и дизъюнкция h) Дистрибутивные законы - конъюнкции относительно дизъюнкции:
- 8. Свойства операций конъюнкция и дизъюнкция h) Дистрибутивные законы - конъюнкции относительно дизъюнкции: - дизъюнкции относительно конъюнкции:
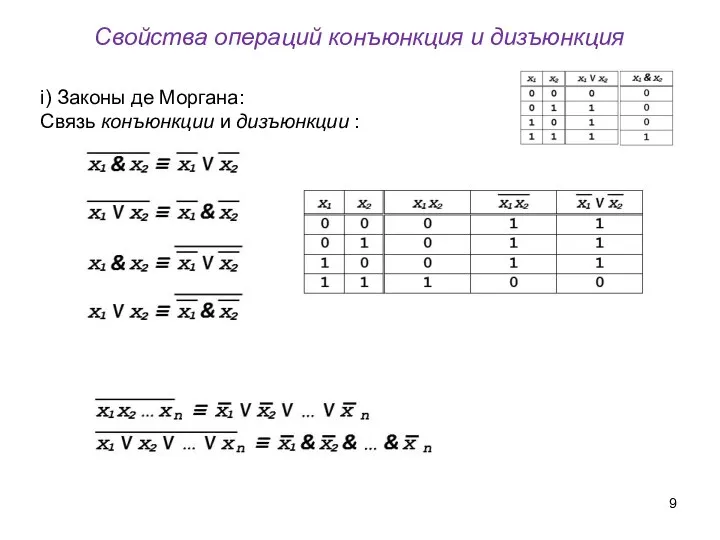
- 9. Свойства операций конъюнкция и дизъюнкция i) Законы де Моргана: Связь конъюнкции и дизъюнкции :
- 10. Свойства операций конъюнкция и дизъюнкция j) Правила склеивания: Доказательство: Пример:
- 11. Свойства операций конъюнкция и дизъюнкция k) Правила поглощения: Доказательство: Пример: Правила склеивания и поглощения могут быть
- 12. Свойства операций штрих Шеффера и стрелка Пирса a) Коммутативный закон: b) Несправедлив ассоциативный закон: c) Выражение
- 13. Свойства операций штрих Шеффера и стрелка Пирса d) Выражение операций отрицание, конъюнкция и дизъюнкция через операцию
- 14. Свойства операций штрих Шеффера и стрелка Пирса Пример: Записать формулу с помощью одной операции штрих Шеффера
- 15. Свойства операций импликация и запрет a) Несправедлив коммутативный закон b) Несправедлив ассоциативный закон c) Выражение операций
- 16. Свойства операций импликация и запрет d) Выражение операций отрицание, конъюнкция и дизъюнкция через операцию импликация доказательство:
- 17. Свойства операций эквивалентность, сложение по модулю два и исключающее ИЛИ a) Справедлив коммутативный закон b) Справедлив
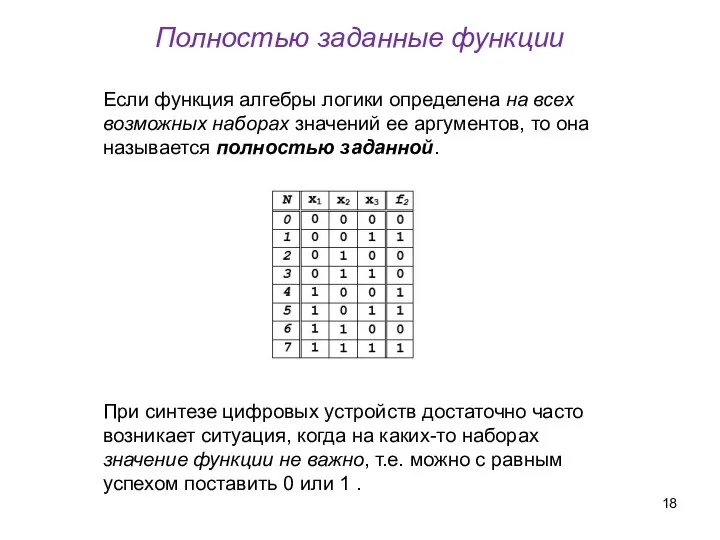
- 18. Полностью заданные функции Если функция алгебры логики определена на всех возможных наборах значений ее аргументов, то
- 19. Частично заданные функции Такие функции называются не полностью определенные или частично заданные функции. Наборы, на которых
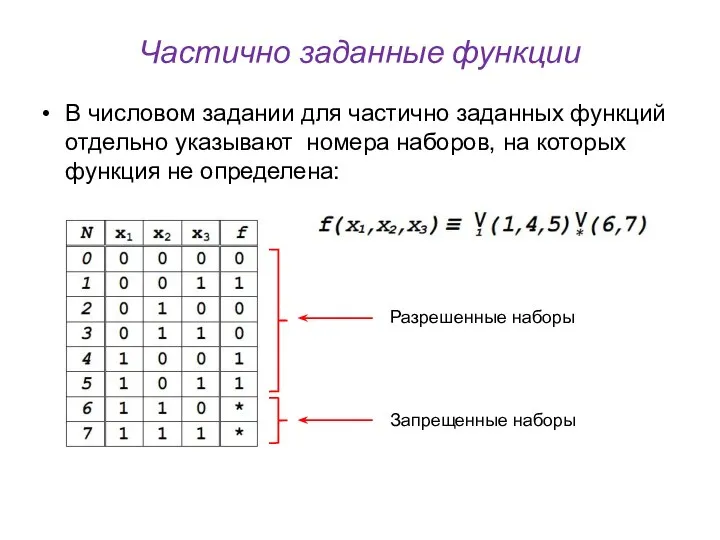
- 20. Частично заданные функции В числовом задании для частично заданных функций отдельно указывают номера наборов, на которых
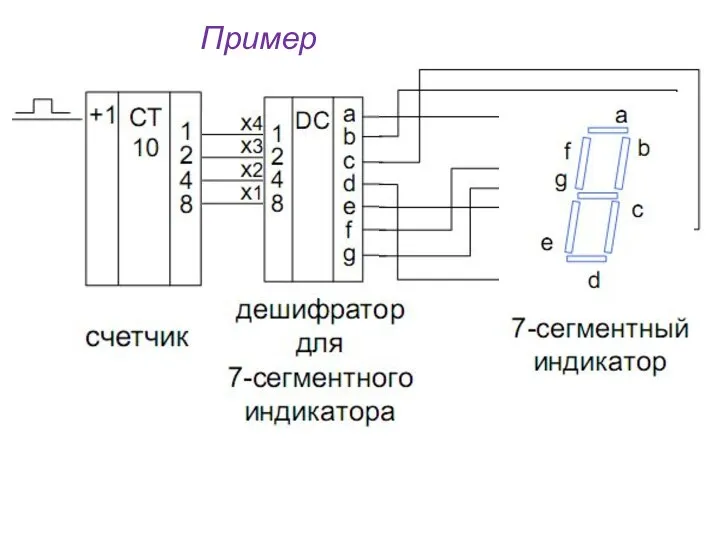
- 21. Пример
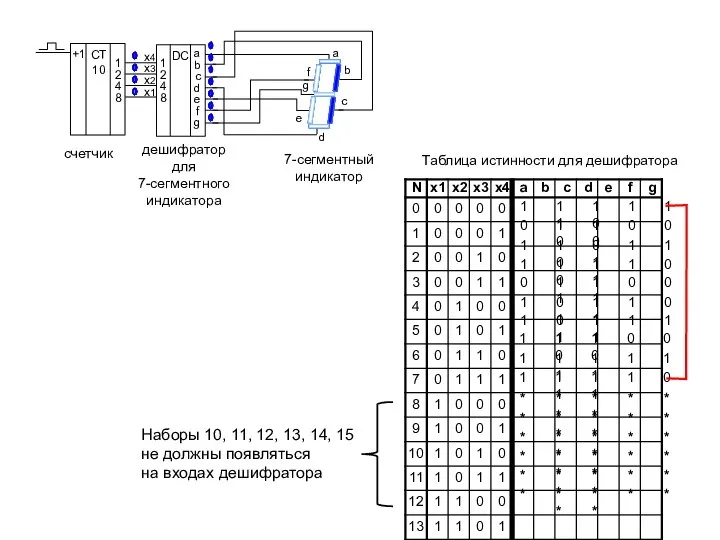
- 22. b c d e f DC a b c d e f g 1 2 4
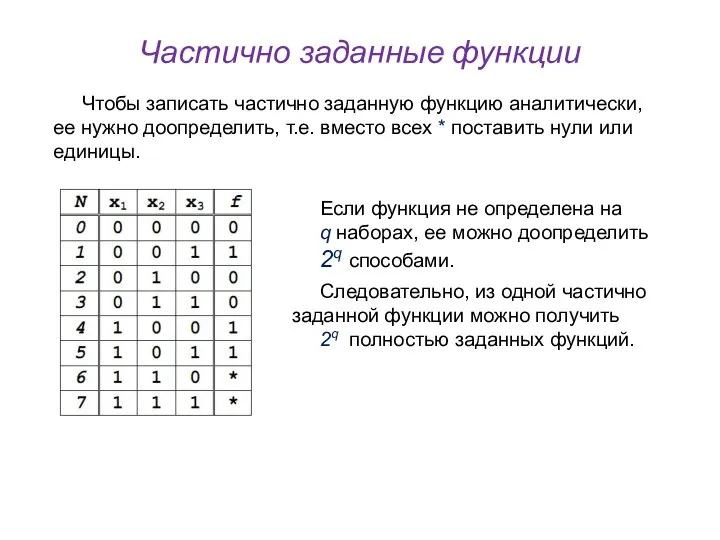
- 23. Частично заданные функции Чтобы записать частично заданную функцию аналитически, ее нужно доопределить, т.е. вместо всех *
- 24. Аналитическая запись функций алгебры логики в базисе И, ИЛИ, НЕ
- 25. Функционально полная система Функционально полная система (базис) – набор некоторых операций (или даже всего одной), который
- 26. Минимизация ФАЛ Нахождение кратчайшей аналитической записи функции алгебры логики в некотором базисе называется минимизацией. Лучше всего
- 27. Элементарной конъюнкцией, или импликантой, называется конъюнкция, состоящая из нескольких аргументов, причем каждый аргумент входит в нее
- 28. Элементарная конъюнкция, в которую входят все аргументы данной функции, называется элементарной конъюнкцией высшего ранга, или минтермом.
- 29. Дизъюнктивной нормальной формой (ДНФ) называется дизъюнкция элементарных конъюнкций. ДНФ для функции f(x1 x2…xn ), состоящая только
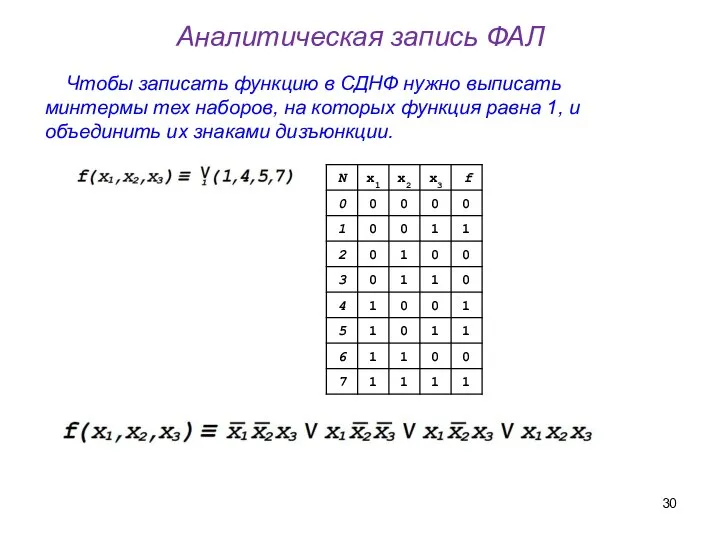
- 30. Чтобы записать функцию в СДНФ нужно выписать минтермы тех наборов, на которых функция равна 1, и
- 31. Упрощение ДНФ может быть достигнуто за счет уменьшения числа входящих в ДНФ элементарных конъюнкций и за
- 32. Чтобы найти СокрДНФ, нужно в СДНФ провести все возможные склеивания. Если из СокрДНФ выбрасывать лишние простые
- 33. Элементарной дизъюнкцией называется дизъюнкция, нескольких аргументов, причем каждый аргумент входит в нее не более одного раза.
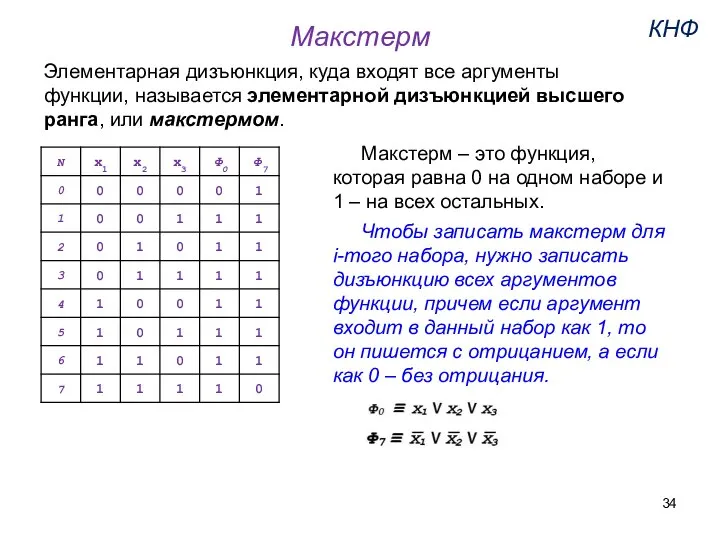
- 34. Элементарная дизъюнкция, куда входят все аргументы функции, называется элементарной дизъюнкцией высшего ранга, или макстермом. Макстерм Макстерм
- 35. Конъюнктивной нормальной формой (КНФ) называется конъюнкция элементарных дизъюнкций. У функции может быть несколько КНФ. КНФ для
- 36. Чтобы записать функцию в СКНФ нужно выписать макстермы тех наборов, на которых функция равна 0, и
- 37. Чтобы найти все простые импликанты (т.е. сокращенную дизъюнктивную нормальную форму), нужно в СДНФ провести все возможные
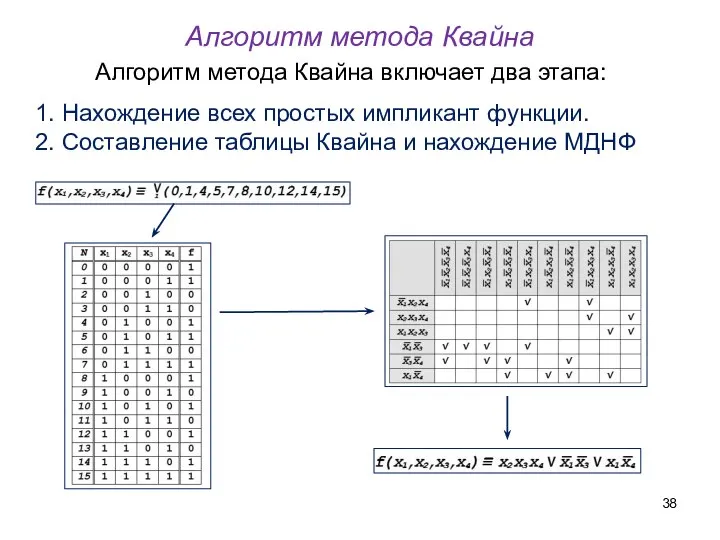
- 38. Алгоритм метода Квайна включает два этапа: 1. Нахождение всех простых импликант функции. 2. Составление таблицы Квайна
- 40. Скачать презентацию

























 Коллинеарные векторы
Коллинеарные векторы Линейные неравенства
Линейные неравенства Правила дифференцирования
Правила дифференцирования Графики тригонометрических функций. 10 класс
Графики тригонометрических функций. 10 класс Логарифмические неравенства
Логарифмические неравенства Параллелепипед. Куб
Параллелепипед. Куб Симметрия в пространстве
Симметрия в пространстве Знакомьтесь, открытые задачи. Мастер-класс
Знакомьтесь, открытые задачи. Мастер-класс Случаи вычитания 12 -
Случаи вычитания 12 - Введение декартовых координат в пространстве. Формулы середины отрезка и расстояния между двумя точками
Введение декартовых координат в пространстве. Формулы середины отрезка и расстояния между двумя точками Измерение углов поворота в радианах. Алгебра 9 класс
Измерение углов поворота в радианах. Алгебра 9 класс Основы алгебры логики
Основы алгебры логики Деление
Деление Презентация на тему Прикладные задачи на экстремумы
Презентация на тему Прикладные задачи на экстремумы  Презентация на тему Квадратные уравнения. Основные свойства
Презентация на тему Квадратные уравнения. Основные свойства  Тригонометрические уравнения. Устный счет
Тригонометрические уравнения. Устный счет Сложение и вычитание чисел с переходом через десяток
Сложение и вычитание чисел с переходом через десяток Построение и анализ графиков в среде Живая геометрия. 9 класс
Построение и анализ графиков в среде Живая геометрия. 9 класс Умножение обыкновенных дробей
Умножение обыкновенных дробей Презентация на тему АЛГЕБРАИЧЕСКИЕ УРАВНЕНИЯ ПРОИЗВОЛЬНЫХ СТЕПЕНЕЙ
Презентация на тему АЛГЕБРАИЧЕСКИЕ УРАВНЕНИЯ ПРОИЗВОЛЬНЫХ СТЕПЕНЕЙ  Свойства сложения и умножения - Презентация_
Свойства сложения и умножения - Презентация_ Линии и углы в окружности
Линии и углы в окружности Презентация_к_уроку_Сложение_и_вычитание_алгебраических_дробей_с
Презентация_к_уроку_Сложение_и_вычитание_алгебраических_дробей_с Формулы преобразования суммы и разности тригонометрических функций в произведение
Формулы преобразования суммы и разности тригонометрических функций в произведение Индивидуальное задание №8. Построение линии пересечения тора и конуса
Индивидуальное задание №8. Построение линии пересечения тора и конуса Задачи на построение
Задачи на построение Геометрия с Дракошей (2 класс)
Геометрия с Дракошей (2 класс) Таблица умножение числа 5
Таблица умножение числа 5