Содержание
- 2. Описание лабораторной установки
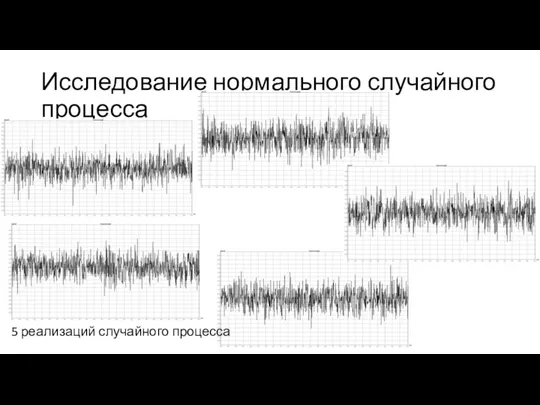
- 3. Исследование нормального случайного процесса 5 реализаций случайного процесса
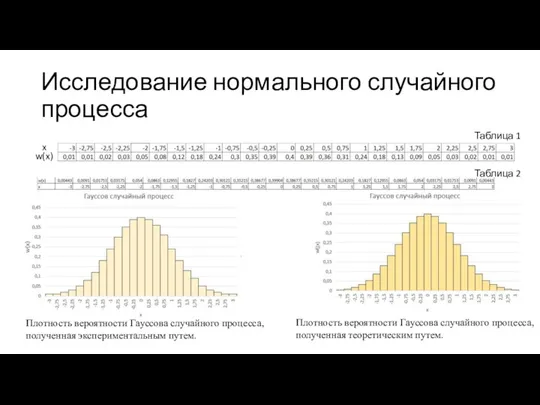
- 4. Исследование нормального случайного процесса Плотность вероятности Гауссова случайного процесса, полученная экспериментальным путем. Плотность вероятности Гауссова случайного
- 5. Вывод Исходя из графиков, можно сделать вывод, что гистограмма плотности вероятности, полученная экспериментальным путем будет схожа
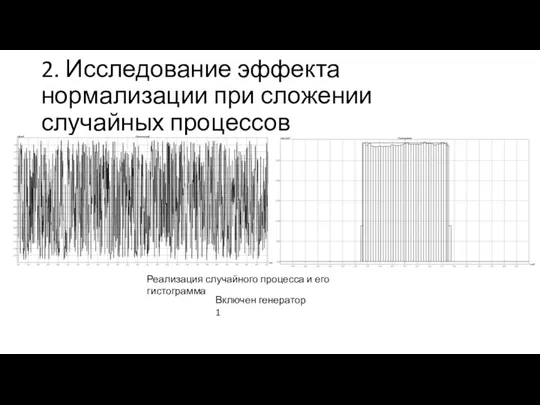
- 6. 2. Исследование эффекта нормализации при сложении случайных процессов Реализация случайного процесса и его гистограмма Включен генератор
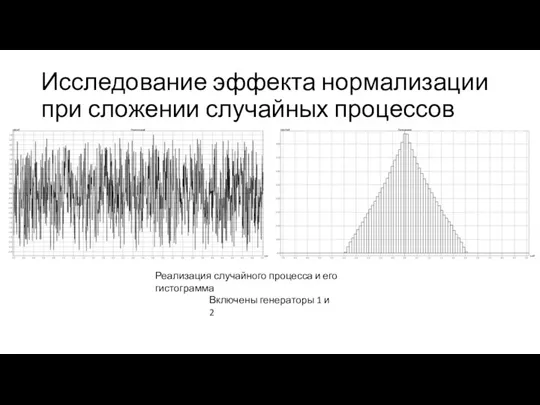
- 7. Исследование эффекта нормализации при сложении случайных процессов Включены генераторы 1 и 2 Реализация случайного процесса и
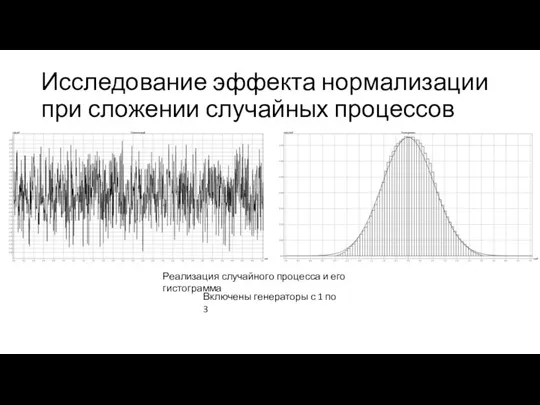
- 8. Исследование эффекта нормализации при сложении случайных процессов Реализация случайного процесса и его гистограмма Включены генераторы с
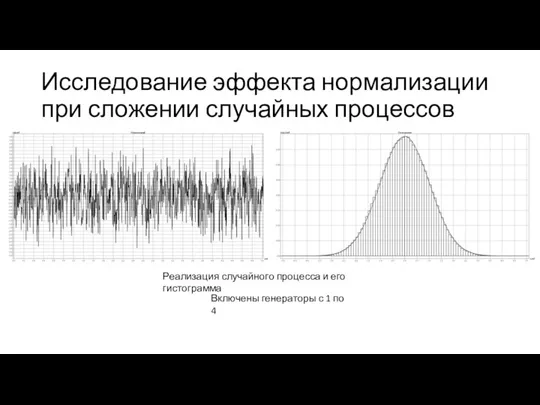
- 9. Исследование эффекта нормализации при сложении случайных процессов Реализация случайного процесса и его гистограмма Включены генераторы с
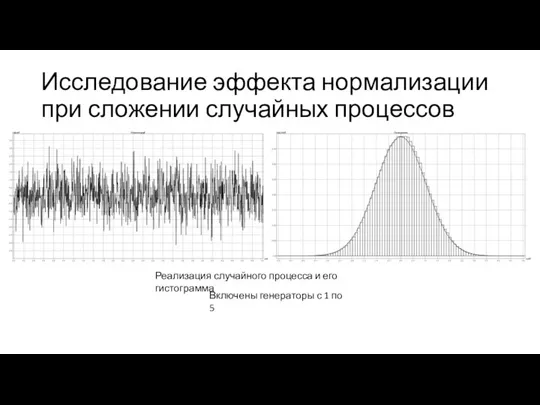
- 10. Исследование эффекта нормализации при сложении случайных процессов Реализация случайного процесса и его гистограмма Включены генераторы с
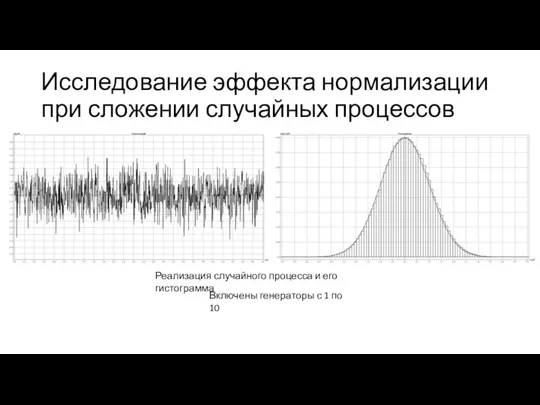
- 11. Исследование эффекта нормализации при сложении случайных процессов Реализация случайного процесса и его гистограмма Включены генераторы с
- 12. Вывод При добавлении в аддитивную смесь сигнала случайного процесса, гистограмма плотности распределения вероятности становится все более
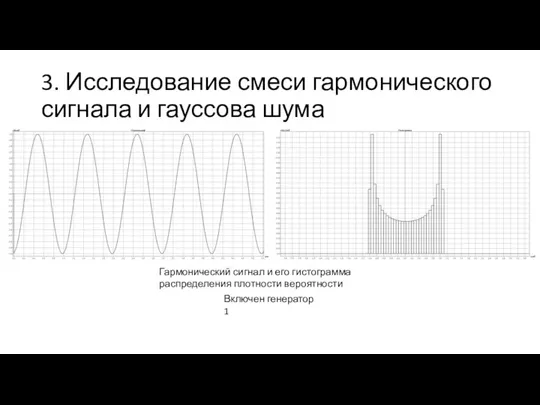
- 13. 3. Исследование смеси гармонического сигнала и гауссова шума Гармонический сигнал и его гистограмма распределения плотности вероятности
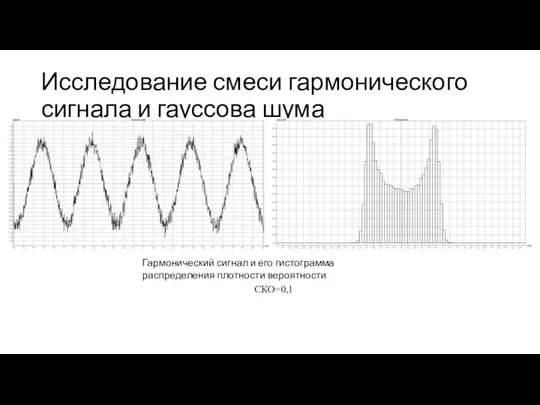
- 14. Исследование смеси гармонического сигнала и гауссова шума Гармонический сигнал и его гистограмма распределения плотности вероятности СКО=0,1
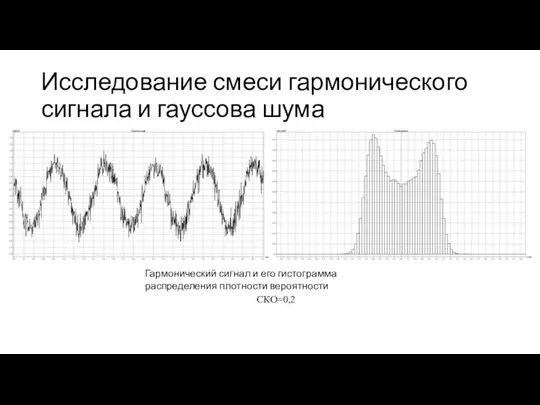
- 15. Исследование смеси гармонического сигнала и гауссова шума Гармонический сигнал и его гистограмма распределения плотности вероятности СКО=0,2
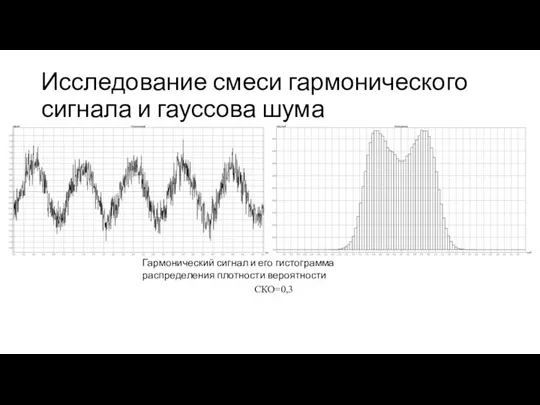
- 16. Исследование смеси гармонического сигнала и гауссова шума Гармонический сигнал и его гистограмма распределения плотности вероятности СКО=0,3
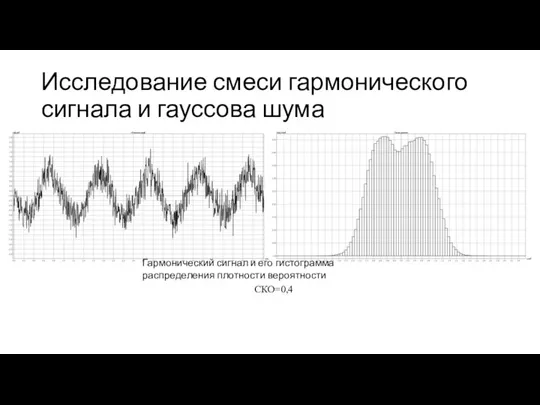
- 17. Исследование смеси гармонического сигнала и гауссова шума Гармонический сигнал и его гистограмма распределения плотности вероятности СКО=0,4
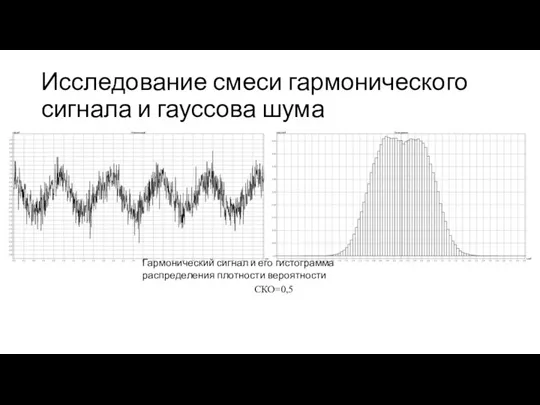
- 18. Исследование смеси гармонического сигнала и гауссова шума Гармонический сигнал и его гистограмма распределения плотности вероятности СКО=0,5
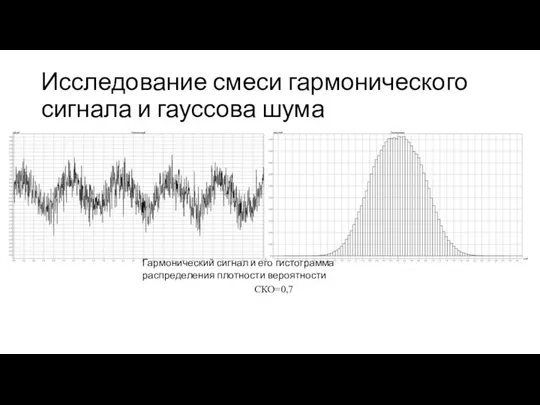
- 19. Исследование смеси гармонического сигнала и гауссова шума Гармонический сигнал и его гистограмма распределения плотности вероятности СКО=0,7
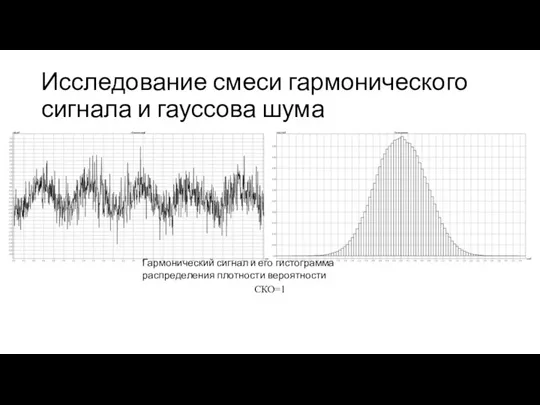
- 20. Исследование смеси гармонического сигнала и гауссова шума Гармонический сигнал и его гистограмма распределения плотности вероятности СКО=1
- 21. Вывод При смешивании гармонического сигнала с шумом, и последующим увеличением СКО, мы наблюдаем, что сигнал на
- 23. Скачать презентацию




 Презентация по математике "Правило умножения для комбинаторных задач" -
Презентация по математике "Правило умножения для комбинаторных задач" -  Окружность. Углы
Окружность. Углы Сократите дробь решите систему, уравнение, упростите выражение и т.д
Сократите дробь решите систему, уравнение, упростите выражение и т.д В мире цветов и плодов. Интегрированный урок биологии и математики
В мире цветов и плодов. Интегрированный урок биологии и математики Порог чувствительности средства измерений
Порог чувствительности средства измерений Отношения рядом стоящих чисел в пределах 10
Отношения рядом стоящих чисел в пределах 10 Процентное содержание компонентов
Процентное содержание компонентов Алгебраический способ решения задач (часть 1)
Алгебраический способ решения задач (часть 1) Интегрированный урок алгебры и экономики. 7 класс
Интегрированный урок алгебры и экономики. 7 класс Презентация на тему Площади многоугольников
Презентация на тему Площади многоугольников  Геометрическая мозаика из правильных одноимённых многоугольников
Геометрическая мозаика из правильных одноимённых многоугольников Презентация на тему Векторы (9 класс)
Презентация на тему Векторы (9 класс)  Угол между векторами
Угол между векторами Страна Математика
Страна Математика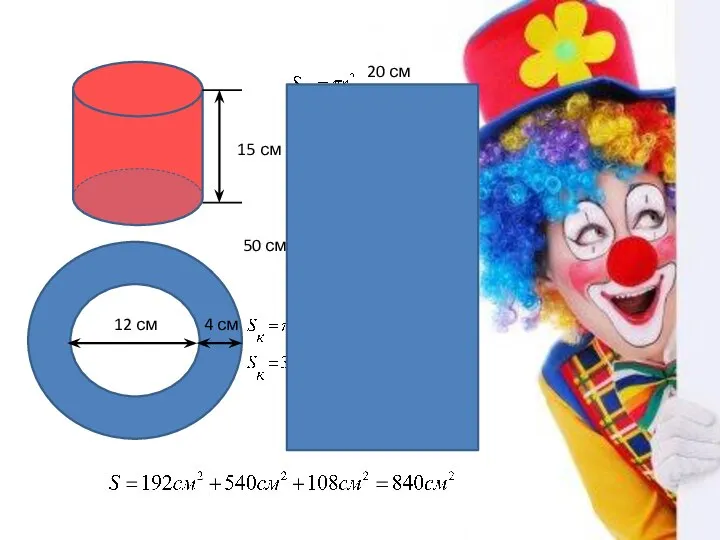 Площадь поверхности цилиндра
Площадь поверхности цилиндра Состав чисел
Состав чисел Задачи на движение в противоположных направлениях
Задачи на движение в противоположных направлениях Неизвестное делимое
Неизвестное делимое Изображение десятичной дроби на координатном луче
Изображение десятичной дроби на координатном луче Задачи на построение
Задачи на построение Тригонометрия
Тригонометрия Линейная корреляция
Линейная корреляция Теория вероятностей
Теория вероятностей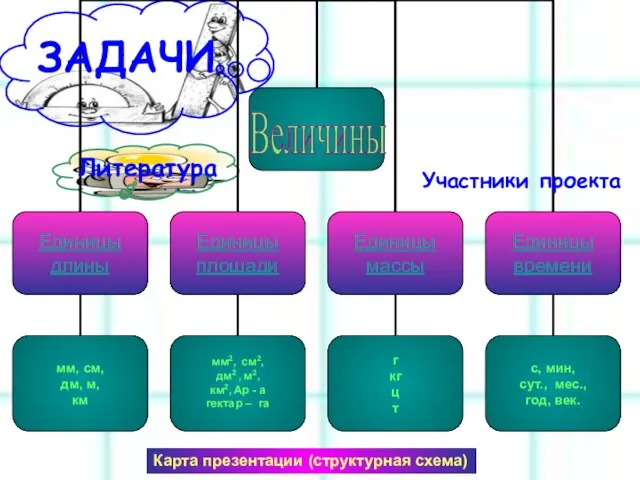 Презентация на тему Величины (4 класс)
Презентация на тему Величины (4 класс)  Знакомство с цифрой 5
Знакомство с цифрой 5 Преобразование выражений с помощью формул сокращенного умножения
Преобразование выражений с помощью формул сокращенного умножения Математические ребусы
Математические ребусы Занятие 1_2022
Занятие 1_2022