Слайд 2Найдите область определения функции:
у= log3x
у= log½(x-3)
у= log0,2(х+2)-1
у= -12log5х
у= log2(4х-1)
у= log5(х2-5х+6)
(0;+∞)
(3;+∞)
(-2;+∞)
(0;+∞)
(¼;+∞)
(-∞;2)U (3;+∞)

Слайд 3Определите метод решения уравнений
log2х=3
log3 (х2+6)= log35х
log2х=-х+1
3log2½х+5log½х-2=0
хlog3х=81

Слайд 4ОСНОВНЫЕ МЕТОДЫ РЕШЕНИЯ УРАВНЕНИЙ
Функционально-графический метод;
Решение по определению;
Метод потенцирования;
Метод логарифмирования;
Метод введения новой переменной.

Слайд 5Решение логарифмических уравнений

Слайд 6Метод потенцирования
Под потенцированием понимается переход от равенства, содержащего логарифмы, к равенству,

не содержащему их:
если , loga f(х) = loga g(х), то f(х) = g(х), f(х)>0, g(х)>0 , а > 0, а≠ 1.
№1552(в)
Слайд 7Метод введения новой переменной
Вводят новую переменную, решают полученное уравнение относительно этой

переменной, а затем возвращаются к переменной х.
№1555 (в)
Слайд 8Проверь себя
Вариант 1 баа
Вариант 2 вба
Вариант 3 агб
Вариант 4 абг








 Формула суммы n первых членов геометрической прогрессии
Формула суммы n первых членов геометрической прогрессии Логарифмические уравнения
Логарифмические уравнения Сочетания
Сочетания Решение уравнений
Решение уравнений Элементы векторной алгебры
Элементы векторной алгебры Нас окружают числа. Факультет космических исследований МГУ имени М.В.Ломоносова
Нас окружают числа. Факультет космических исследований МГУ имени М.В.Ломоносова Симплекс метод. Лекция 5
Симплекс метод. Лекция 5 Задачи на построение сечений. 10 класс
Задачи на построение сечений. 10 класс Квадратные уравнения
Квадратные уравнения Презентация на тему Математика в профессиях (11 класс)
Презентация на тему Математика в профессиях (11 класс)  Четырехугольники
Четырехугольники Построение сечений
Построение сечений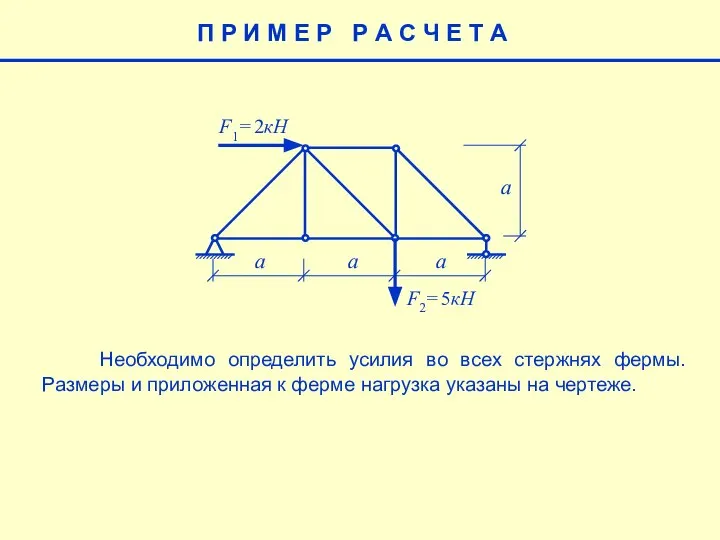 Методы расчета ферм
Методы расчета ферм Степень с натуральным показателем
Степень с натуральным показателем Формы графического изображения. (Лекция 3)
Формы графического изображения. (Лекция 3) Целое уравнение и его корни. 9 класс
Целое уравнение и его корни. 9 класс Пифагор. Пифагорейская школа
Пифагор. Пифагорейская школа Презентация на тему Построение треугольника по трем элементам
Презентация на тему Построение треугольника по трем элементам  Своя игра 1
Своя игра 1 Путешествие по морям
Путешествие по морям Из истории геометрии
Из истории геометрии Многозначная логика
Многозначная логика Задачи на движение в противоположных направлениях
Задачи на движение в противоположных направлениях Деление с остатком
Деление с остатком Площади. Теорема Пифагора. Урок - зачёт 8 класс
Площади. Теорема Пифагора. Урок - зачёт 8 класс Виды углов.Измерение углов
Виды углов.Измерение углов Опыт по получению тени от различных фигур
Опыт по получению тени от различных фигур Тригонометрические тождества
Тригонометрические тождества