Слайд 3При изучении какого-либо признака, присущего всем элементам совокупности, представляет интерес распределение его

значений среди этих элементов. То есть, какое количество, или какая их доля, обладает некоторым конкретным значением рассматриваемого признака. Или для какого количества элементов значение рассматриваемого признака попадает в интересующий наблюдателя интервал значений.
Если же нас интересуют события, которые произойдут в будущем то, в этом случае мы можем говорить, лишь о вероятности того, что данное событие произойдет или не произойдет. Например, в середине лета, мы с большой вероятностью знаем, что на следующий день не выпадет снег. Но, жизненный опыт подсказывает, что природа иногда преподносит сюрпризы, а это значит что событие «утром выпал снег» возможно и летом, но оно маловероятно. Причина наших сомнений заключается в том, что мы не можем знать все факторы, которые влияют на то или иное событие. То есть, вероятность это не свойство природы, а результат неполноты наших знаний о ней.













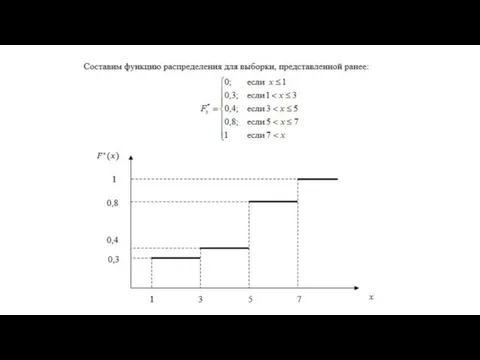


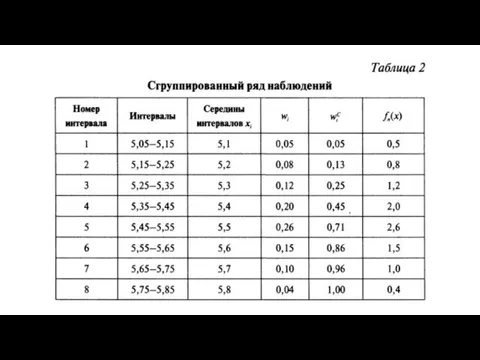
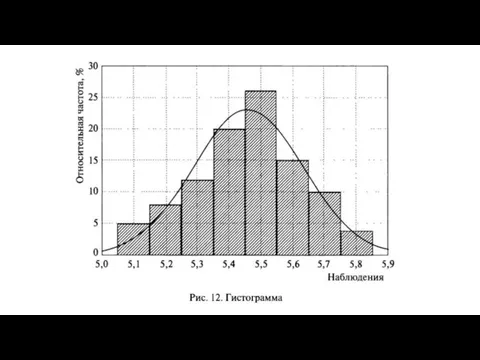





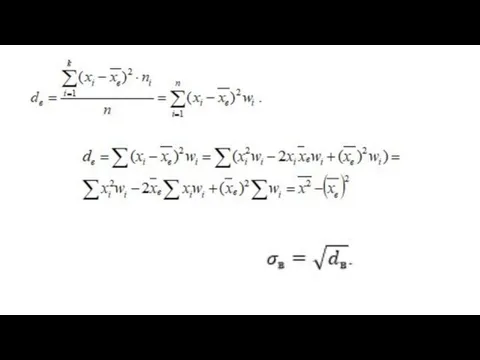










































 Среднее арифметическое
Среднее арифметическое Метод неопределенных коэффициентов
Метод неопределенных коэффициентов Среднее арифметическое
Среднее арифметическое Узоры и орнаменты на посуде
Узоры и орнаменты на посуде Игра Что? Где? Почему?
Игра Что? Где? Почему? Интегрирование тригонометрических функций
Интегрирование тригонометрических функций Пирамида
Пирамида Исаак Ньютон
Исаак Ньютон Колесо истории математики
Колесо истории математики Высота, биссектриса и медиана треугольника
Высота, биссектриса и медиана треугольника Методология математического моделирования
Методология математического моделирования Тест. Реши. И ты станешь уважать себя
Тест. Реши. И ты станешь уважать себя Поле чудес. 3 класс
Поле чудес. 3 класс Нахождение коэффициентов квадратичной функции по графику
Нахождение коэффициентов квадратичной функции по графику Многогранники. Призма
Многогранники. Призма Обыкновенные дроби. 5 класс
Обыкновенные дроби. 5 класс Prezentatsia
Prezentatsia Гарри Потер. Игра по математике и физике
Гарри Потер. Игра по математике и физике Треугольники. Задача
Треугольники. Задача Производная. Физический смысл производной. Приращение аргумента и приращение функции. Задания
Производная. Физический смысл производной. Приращение аргумента и приращение функции. Задания Презентация на тему Квадратичная функция
Презентация на тему Квадратичная функция  Повторение. Дроби
Повторение. Дроби Решение задач на движение
Решение задач на движение Округление десятичных дробей
Округление десятичных дробей Перпендикулярность плоскостей. 10 класс
Перпендикулярность плоскостей. 10 класс Элементы комбинаторики
Элементы комбинаторики Урок математики в 10 классе по теме Пирамида
Урок математики в 10 классе по теме Пирамида Сокращение дробей. Тождество
Сокращение дробей. Тождество