Содержание
- 2. ЗАДАЧИ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ Что общего и чем отличаются ТВ и МС? ТВ: разработка методов нахождения вероятностей
- 3. разрабатывает методы, позволяющие по статистическим данным делать выбор одного из нескольких, противоречащих друг другу, предположений (гипотез)
- 4. Особенность идей и методов математической статистики — универсальность, возможность использования в различных приложениях.
- 5. ОСНОВНЫЕ ПОНЯТИЯ МС Генеральная совокупность Выборка Вариационный ряд Теоретическая функция распределения
- 6. ГЕНЕРАЛЬНАЯ СОВОКУПНОСТЬ Пусть исследуется некоторая совокупность объектов, каждому из которых ставится в соответствие некоторая числовая функция
- 7. Практически, мы отождествляем наблюдаемые объекты и сопоставляемые им случайные величины, абстрагируясь от физической природы объектов. Поэтому
- 8. Выборка В ходе каждого из испытаний мы случайным образом выбираем один из элементов генеральной совокупности и
- 9. ВЫБОРКИ ДОЛЖНЫ БЫТЬ РЕПРЕЗЕНТАТИВНЫМИ Т.Е. Представительными, — должны давать обоснованное представление о генеральной совокупности. Чтобы обеспечить
- 10. Теоретическая функция распределения Рассмотрим выборку единичного объема X1 . Поскольку выбор случаен, то X1 – случайная
- 11. С точки зрения теории вероятностей выборку можно трактовать как совокупность независимых, одинаково распределенных случайных величин с
- 12. Простейшие статистические преобразования
- 13. Вариационный и статистический ряды Вариационный ряд X(1),…, X(n) представляет собой ту же выборку X1,…,Xn, но расположенную
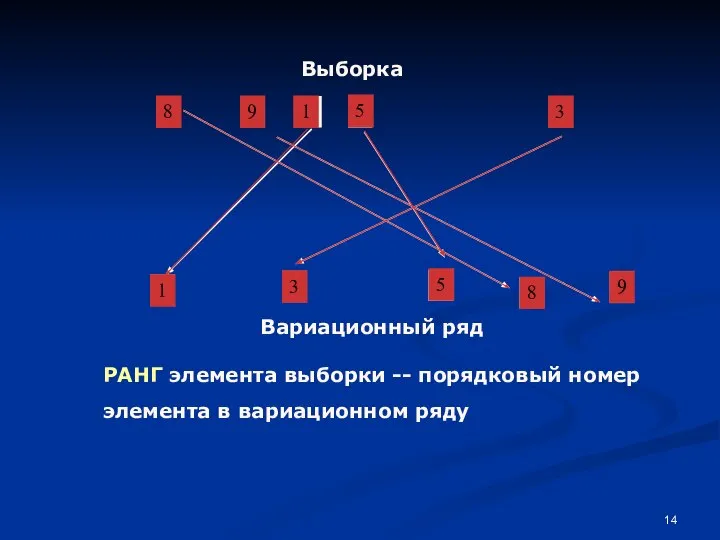
- 14. Выборка Вариационный ряд РАНГ элемента выборки -- порядковый номер элемента в вариационном ряду
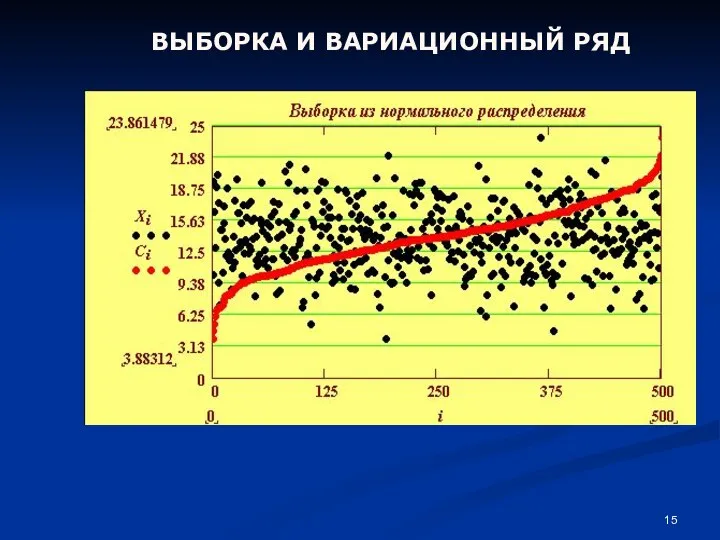
- 15. ВЫБОРКА И ВАРИАЦИОННЫЙ РЯД
- 16. Если среди элементов выборки (вариационного ряда) есть одинаковые, то наряду с ВАРИАЦИОННЫМ рядом используется СТАТИСТИЧЕСКИЙ РЯД
- 17. Статистический ряд Z1
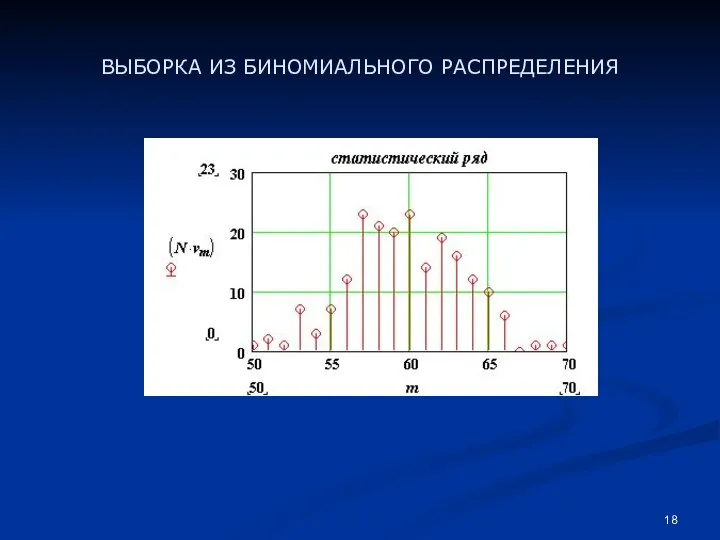
- 18. ВЫБОРКА ИЗ БИНОМИАЛЬНОГО РАСПРЕДЕЛЕНИЯ
- 19. СТАТИСТИКИ Статистика S --- это произвольная измеримая k-мерная функция от выборки, не содержащая неизвестных параметров распределений.
- 20. Достаточные статистики --- такие, которые содержат всю ту информацию о теоретической функции распределения, что и выборка
- 21. ЭМПИРИЧЕСКАЯ ФУНКЦИЯ РАСПРЕДЕЛЕНИЯ (ЭФР)--- аналог теоретической функции: Fe(x) = mx / n где mx --- число
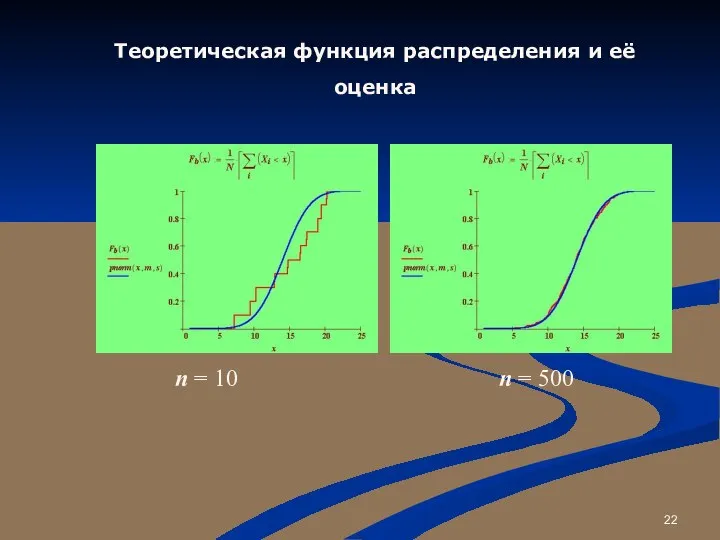
- 22. Теоретическая функция распределения и её оценка n = 10 n = 500
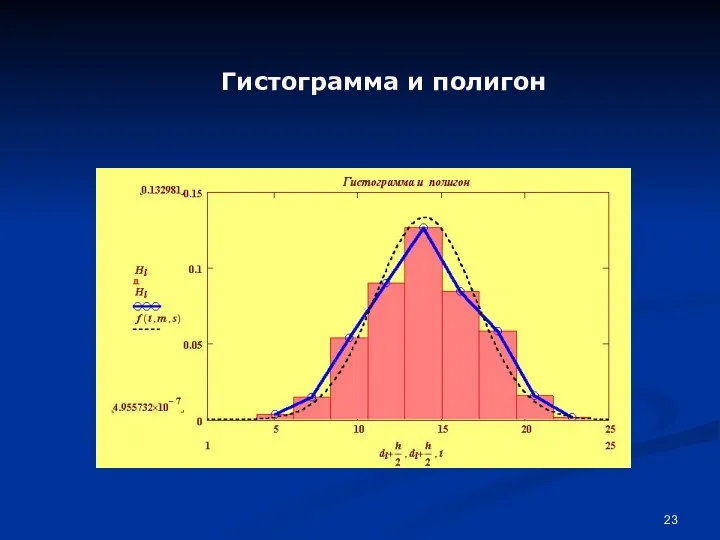
- 23. Гистограмма и полигон
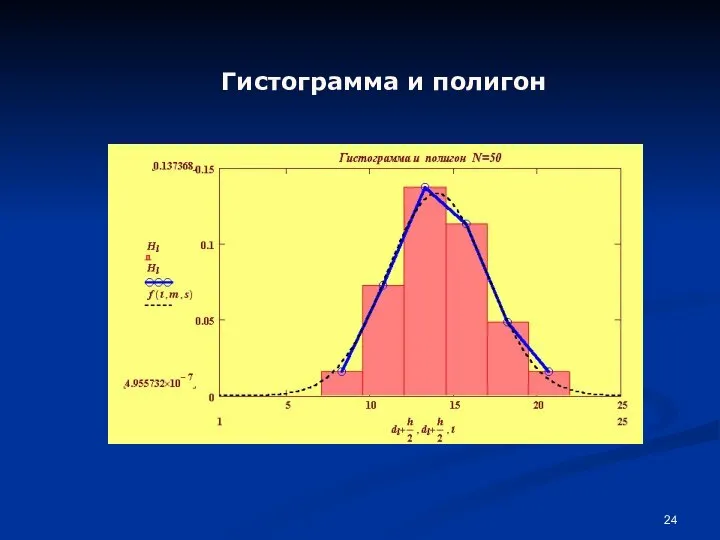
- 24. Гистограмма и полигон
- 26. Скачать презентацию

















 Натуральные и целые числа. Проверочная работа
Натуральные и целые числа. Проверочная работа Арксинус и уравнение вида sinx=a
Арксинус и уравнение вида sinx=a Геометрия в живописи
Геометрия в живописи Основы моделирования
Основы моделирования Правильные многогранники
Правильные многогранники Прямоугольный треугольник
Прямоугольный треугольник Решение задач с применением раскрасок
Решение задач с применением раскрасок Логарифмические уравнения
Логарифмические уравнения Свойства предметов (часть 2)
Свойства предметов (часть 2) Графический способ решения систем уравнений
Графический способ решения систем уравнений Практические задания на применение формул сокращённого умножения
Практические задания на применение формул сокращённого умножения Интерактивный тренажёр. 4 класс
Интерактивный тренажёр. 4 класс Альтернативные издержки и кривая производственных возможностей
Альтернативные издержки и кривая производственных возможностей Сравнение чисел
Сравнение чисел Устный счет. Пропорция
Устный счет. Пропорция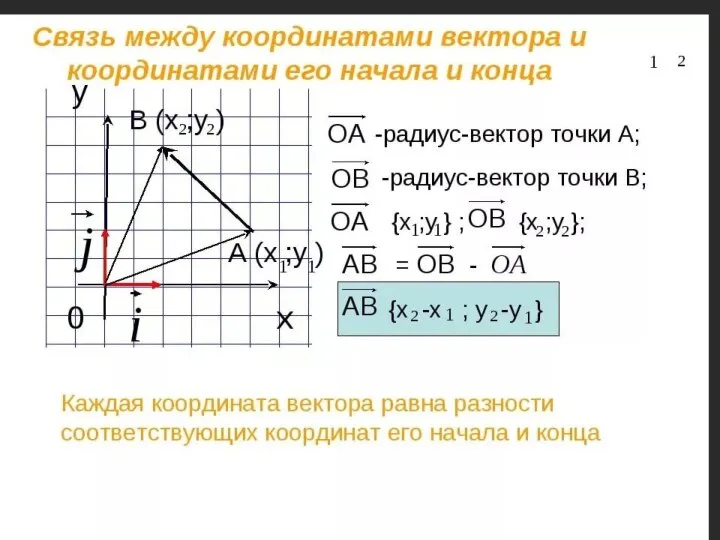 Векторы
Векторы Понятие логарифма
Понятие логарифма Игра
Игра Параллельные прямые
Параллельные прямые Сложение однозначных чисел с переходом через десяток вида +8, +9 (часть 1)
Сложение однозначных чисел с переходом через десяток вида +8, +9 (часть 1) Аналитическая панель
Аналитическая панель Обыкновенные дифференциальные уравнения
Обыкновенные дифференциальные уравнения Цифровые устройства. Логические функции и их минимизация
Цифровые устройства. Логические функции и их минимизация Составление переводной работы по алгебре в формате ЕГЭ, 2017-2018 учебный год
Составление переводной работы по алгебре в формате ЕГЭ, 2017-2018 учебный год Золотое сечение
Золотое сечение Булева алгебра
Булева алгебра Дифференциальные уравнения
Дифференциальные уравнения Степень с отрицательным показателем
Степень с отрицательным показателем