Содержание
- 2. Образование - это не изучение фактов, а тренировка мышления Альберт Эйнштейн Образование – то, что остается
- 3. Математика — фундаментальная наука, предоставляющая (общие) языковые средства другим наукам; тем самым она выявляет их структурную
- 4. Гуманитарный потенциал математики 1. Математика «ум в порядок приводит» - влияние математики на формирование мышления и
- 5. Возникновение математических понятий. Развитие понятия числа. Числа от натуральных до вещественных (и дальше) Возникновение арифметических операций.
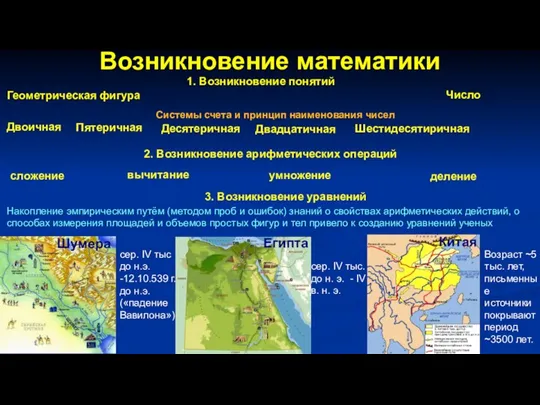
- 6. Возникновение математики 1. Возникновение понятий Геометрическая фигура Число идеализации реальных объектов и множеств однородных объектов -
- 7. Возникновение математики 1. Возникновение понятий Геометрическая фигура Число идеализации реальных объектов и множеств однородных объектов Системы
- 8. Возникновение математики 1. Возникновение понятий Геометрическая фигура Число Появление счёта и измерения позволили сравнивать различные числа,
- 9. Возникновение математики 1. Возникновение понятий Геометрическая фигура Число Появление счёта и измерения позволили сравнивать различные числа,
- 10. Возникновение математики 1. Возникновение понятий Геометрическая фигура Число Когда понятие абстрактного числа окончательно утвердилось, следующей ступенью
- 11. Возникновение математики 1. Возникновение понятий Геометрическая фигура Число отделение части множества сложение 2. Возникновение арифметических операций
- 12. Возникновение математики 1. Возникновение понятий Геометрическая фигура Число отделение части множества сложение 2. Возникновение арифметических операций
- 13. Возникновение математики 1. Возникновение понятий Геометрическая фигура Число отделение части множества сложение 2. Возникновение арифметических операций
- 14. Возникновение математики 1. Возникновение понятий Геометрическая фигура Число сложение 2. Возникновение арифметических операций вычитание умножение деление
- 15. Возникновение математики 1. Возникновение понятий Геометрическая фигура Число сложение 2. Возникновение арифметических операций вычитание умножение деление
- 16. Возникновение математики 1. Возникновение понятий Геометрическая фигура Число Системы счета и принцип наименования чисел Двоичная Десятеричная
- 17. Фрагмент папируса Райнда. Царь разделил землю между египтянами, дав каждому по равному прямоугольному участку; из этого
- 18. В папирусах встречаются задачи на арифметическую и геометрическую прогрессии. нахождение точно площади поля прямоугольной, треугольной и
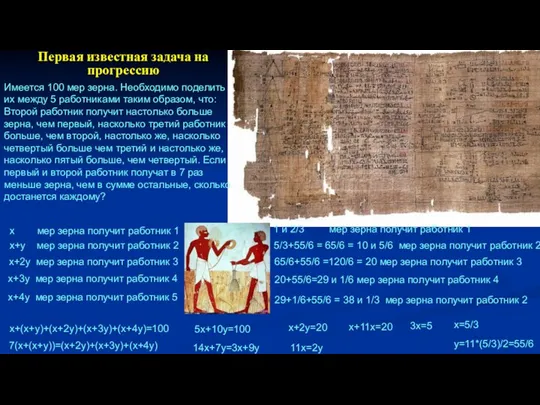
- 19. Имеется 100 мер зерна. Необходимо поделить их между 5 работниками таким образом, что: Второй работник получит
- 20. Диофант Александрийский – «отец алгебры», живший предположительно в III в. н. э. В его книге «Арифметика»
- 21. Два человека и получили неизвестное количество монет. Их надо определить из условия: если добавить первому половину
- 22. Геометрическая интерпретация системы линейных уравнений Уравнения с двумя переменными вида: Ах+Ву+С=0 описывают на координатной плоскости Оху
- 23. 12 8 0 145 0 8 0 34 0 0 4 11 Древний Китай Метод ″фан-чэн″
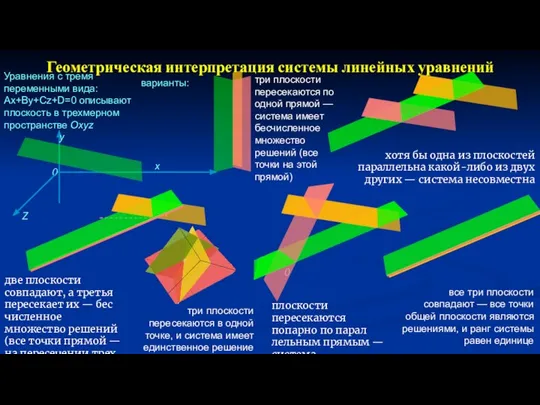
- 24. Геометрическая интерпретация системы линейных уравнений Уравнения с тремя переменными вида: Ах+Ву+Сz+D=0 описывают плоскость в трехмерном пространстве
- 26. Скачать презентацию



















 Задача на арифметическую прогрессию (1)
Задача на арифметическую прогрессию (1) Логический элемент
Логический элемент Тригонометрические уравнения
Тригонометрические уравнения Сложение и вычитание алгебраических дробей
Сложение и вычитание алгебраических дробей Основные задачи и область применения дискретной математики
Основные задачи и область применения дискретной математики Симетричні фігури
Симетричні фігури Лекция 5. Плоские и планарные графы
Лекция 5. Плоские и планарные графы Презентация на тему Объем прямой призмы
Презентация на тему Объем прямой призмы  Стереометрия. 1
Стереометрия. 1 Сравнение чисел
Сравнение чисел Физический и механический смысл производных. Использование производной в физике, механике
Физический и механический смысл производных. Использование производной в физике, механике Решение задач
Решение задач Презентация на тему Является ли система координат чисто математическим понятием
Презентация на тему Является ли система координат чисто математическим понятием  Аналоги теореми порівняння Колмогорова та їх застосування
Аналоги теореми порівняння Колмогорова та їх застосування Больше, меньше, столько же
Больше, меньше, столько же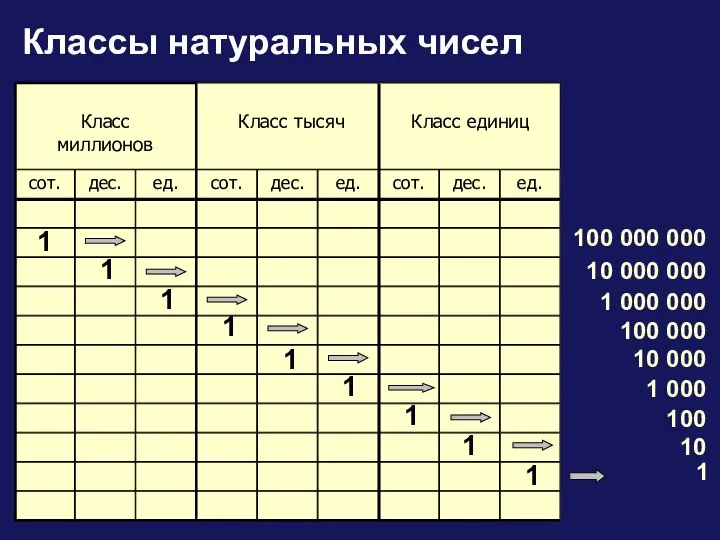 Классы натуральных чисел
Классы натуральных чисел Исследование функции на монотонность
Исследование функции на монотонность Построить линейный угол двугранного угла
Построить линейный угол двугранного угла Элементы комбинаторики
Элементы комбинаторики Сложение с переходом через десяток
Сложение с переходом через десяток Сумма n первых членов геометрической прогрессии (9 класс)
Сумма n первых членов геометрической прогрессии (9 класс) Действия с десятичными дробями
Действия с десятичными дробями Показательные уравнения и неравенства
Показательные уравнения и неравенства Тригонометрические уравнения Однородные тригонометрические уравнения
Тригонометрические уравнения Однородные тригонометрические уравнения Использование свойств действий при вычислениях. Наглядный материал к уроку
Использование свойств действий при вычислениях. Наглядный материал к уроку Математический хоккей
Математический хоккей Арифметический корень натуральной степени
Арифметический корень натуральной степени Введение в математическую логику и теорию множеств
Введение в математическую логику и теорию множеств