Слайд 3ГЕОМЕТРИЧЕСКИЙ СМЫСЛ ПРОИЗВОДНОЙ
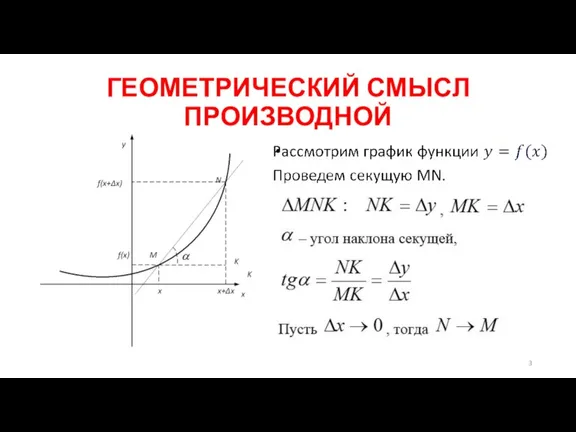
Слайд 4ГЕОМЕТРИЧЕСКИЙ СМЫСЛ ПРОИЗВОДНОЙ
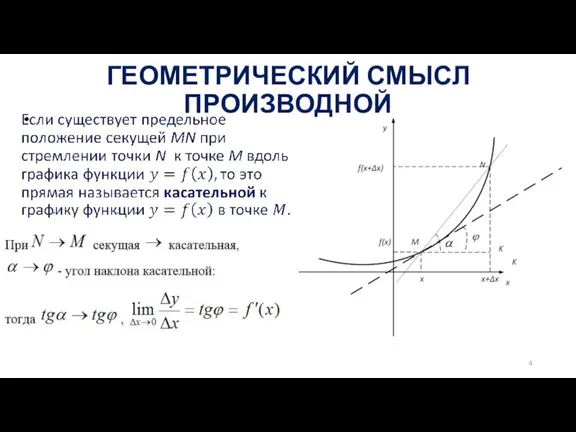
Слайд 6Производная и непрерывность функции
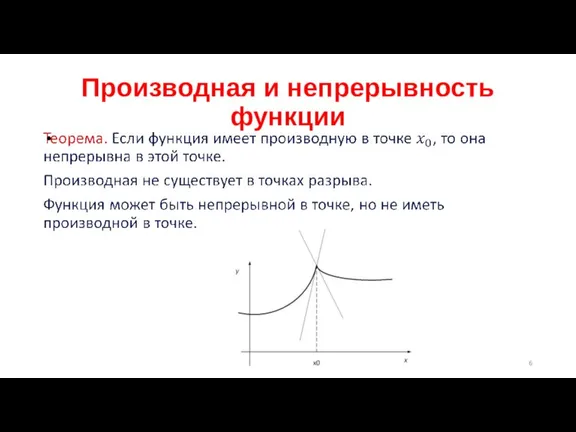
Слайд 8 ПРАВИЛА ВЫЧИСЛЕНИЯ ПРОИЗВОДНЫX
Если и имеют производные в точке x, то этой

точке справедливы равенства:
если
если
Слайд 9ПРОИЗВОДНЫЕ ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ

Слайд 10ПРОИЗВОДНЫЕ ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ

Слайд 11ПРОИЗВОДНЫЕ ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ
в)Аналогично получим .
г) Тогда, так как , то применяя правила

дифференцирования, получим
Аналогично получим
Слайд 12 ТАБЛИЦА ПРОИЗВОДНЫХ ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ
Степенные функции:
Показательные функции:
Логарифмические функции:

Слайд 13 ТАБЛИЦА ПРОИЗВОДНЫХ ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ
5. Тригонометрические функции:
6. Обратные тригонометрические функции:

Слайд 14 ПРАВИЛА ВЫЧИСЛЕНИЯ ПРОИЗВОДНЫX
6. Вычисление сложной функции (Правило цепочки).
Если функция имеет в

некоторой точке x производную
, а функция имеет при соответствующем значении u
производную , тогда сложная функция
имеет в указанной точке x производную, вычисляемую по формуле:
Слайд 15 Примеры вычисления производныx
1.
Примеры:

Слайд 16 Примеры вычисления производныx
2.
Примеры:

Слайд 17 Примеры вычисления производныx
3.
Примеры:

Слайд 18 Примеры вычисления производныx
4.
Примеры:

Слайд 20 Правило дифференцирования степенно-показательной функции
Пусть функция имеет степенно-показательный вид:
Прологарифмируем функцию:
Продифференцируем:
Откуда:

Слайд 21 Правило дифференцирования степенно-показательной функции
Пример.
Прологарифмируем функцию:
Продифференцируем:
Откуда:

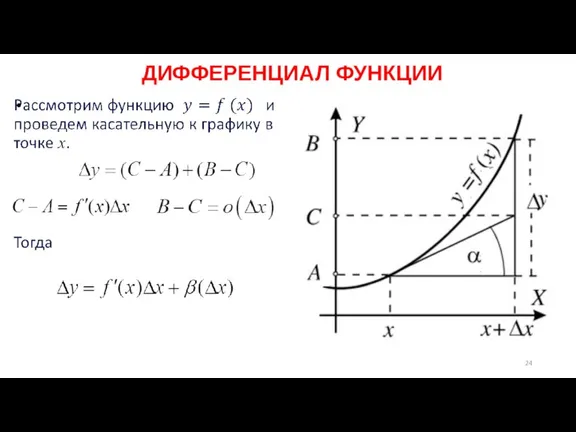
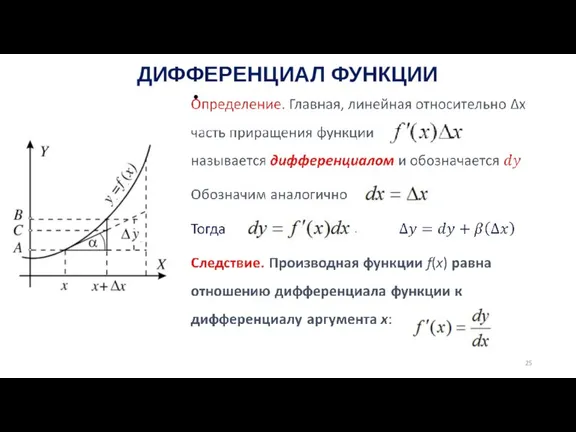
Слайд 26 ДИФФЕРЕНЦИАЛ ФУНКЦИИ
Рассмотрим поведение обоих частей при
Видно, что при функция
убывает быстрее,
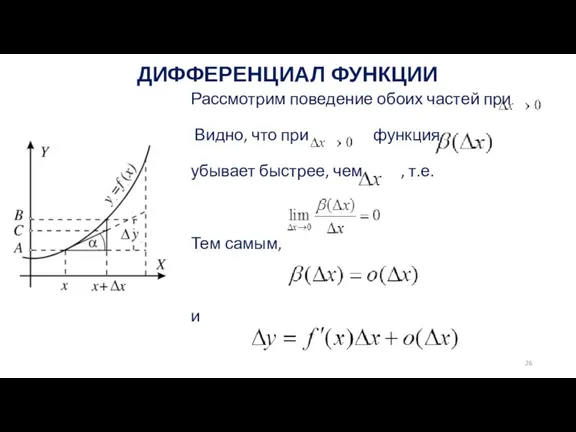
чем , т.е.
Тем самым,
и
Слайд 27 РАСКРЫТИЕ НЕОПРЕДЕЛЕННОСТЕЙ
Правило Лопиталя
Теорема Лопиталя. Пусть функции f(x) и g(x) определены и

имеют производные f '(x) и g '(x) ≠ 0 в некоторой окрестности точки a, кроме быть может самой точки a, и пусть
или
Тогда, если существует предел отношения производных этих функций, то существует предел отношения самих функций и
Слайд 28 РАСКРЫТИЕ НЕОПРЕДЕЛЕННОСТЕЙ
Правило Лопиталя
Примеры.
1.
2. Правило Лопиталя может применяться несколько раз.

Слайд 29 РАСКРЫТИЕ НЕОПРЕДЕЛЕННОСТЕЙ
Правило Лопиталя
Применение правила Лопиталя к неопределенности .
Применение правила Лопиталя к

неопределенности .
Используем основное логарифмическое тождество
Слайд 30 Основные теоремы дифференциального исчисления
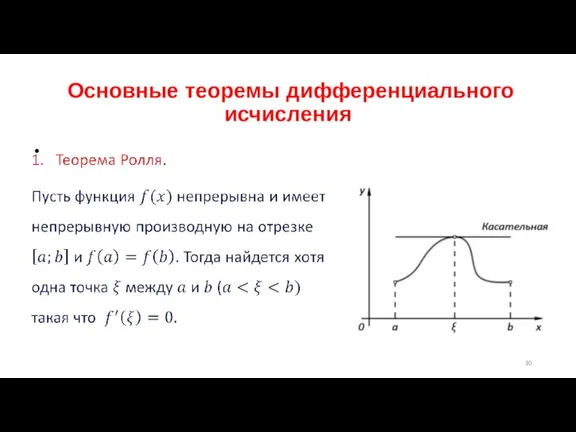
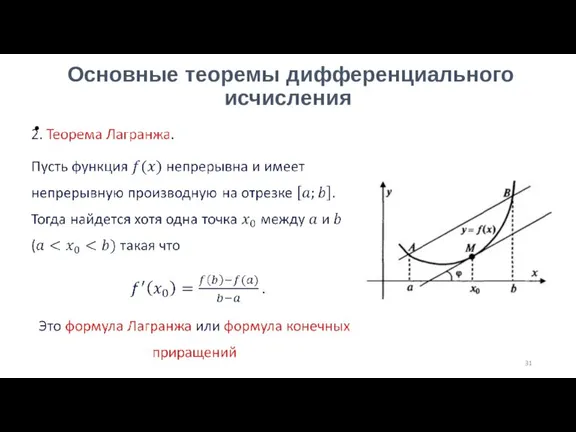
Слайд 31 Основные теоремы дифференциального исчисления




























 Путешествие в город Дробей на проспект Умножения. 6 класс
Путешествие в город Дробей на проспект Умножения. 6 класс Действительный анализ. Теорема Лебега (примеры). Измеримые множества
Действительный анализ. Теорема Лебега (примеры). Измеримые множества Как умножали египтяне
Как умножали египтяне Площадь многоугольника
Площадь многоугольника Решение систем неравенств с одной переменной
Решение систем неравенств с одной переменной Оценка математического ожидания и дисперсии отклика в отдельных точках факторного пространства
Оценка математического ожидания и дисперсии отклика в отдельных точках факторного пространства Полигон частот в математической статистике
Полигон частот в математической статистике Лінейныя ўраўненні з адной зменнай
Лінейныя ўраўненні з адной зменнай Расчёт скорости официанта от кассы до столика
Расчёт скорости официанта от кассы до столика Объём тела
Объём тела Теорема о плоскости, касательной к шару
Теорема о плоскости, касательной к шару Площадь круга и секторов
Площадь круга и секторов Куб
Куб Корень степени n
Корень степени n Построение биссектрисы угла. Билеты
Построение биссектрисы угла. Билеты Урок математики 20.09
Урок математики 20.09 Презентация на тему РЕШЕНИЕ ДРОБНЫХ РАЦИОНАЛЬНЫХ УРАВНЕНИЙ
Презентация на тему РЕШЕНИЕ ДРОБНЫХ РАЦИОНАЛЬНЫХ УРАВНЕНИЙ  Занимательные математические задания
Занимательные математические задания Сравнение групп предметов. Свойства предметов (1 класс)
Сравнение групп предметов. Свойства предметов (1 класс) Математическая модель колонны многокомпонентной ректификации. Лекция 9
Математическая модель колонны многокомпонентной ректификации. Лекция 9 Производная в заданиях уровня В. ЕГЭ
Производная в заданиях уровня В. ЕГЭ Неопределенный интеграл
Неопределенный интеграл Презентация на тему Простые числа
Презентация на тему Простые числа  История г. Колпашева в примерах и задачах
История г. Колпашева в примерах и задачах Сочетания. Свойства сочетаний. Бином Ньютона
Сочетания. Свойства сочетаний. Бином Ньютона Основные понятия теории вероятностей
Основные понятия теории вероятностей Возрастание и убывание функций. Экстремумы
Возрастание и убывание функций. Экстремумы Памятка по оформлению краткой записи к задачам (1 класс)
Памятка по оформлению краткой записи к задачам (1 класс)