Содержание
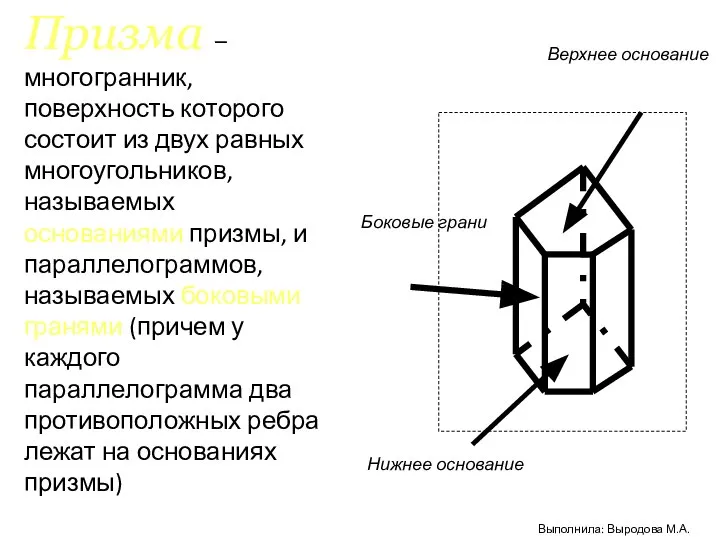
- 2. Призма – многогранник, поверхность которого состоит из двух равных многоугольников, называемых основаниями призмы, и параллелограммов, называемых
- 3. Призма «Призма есть телесная фигура,заключенная между плоскостями, из которых две противоположные равны и параллельны, остальные же
- 4. В 18 веке Тейлор дал такое определение призмы: «Призма - это многогранник, у которого все грани,
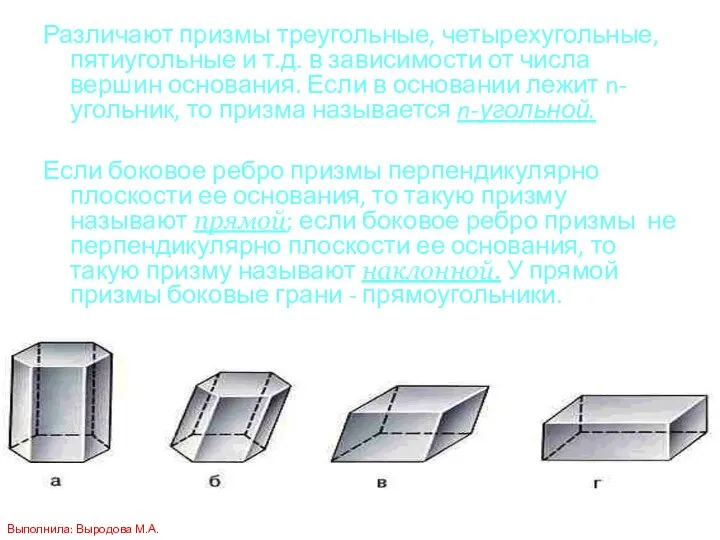
- 5. Различают призмы треугольные, четырехугольные, пятиугольные и т.д. в зависимости от числа вершин основания. Если в основании
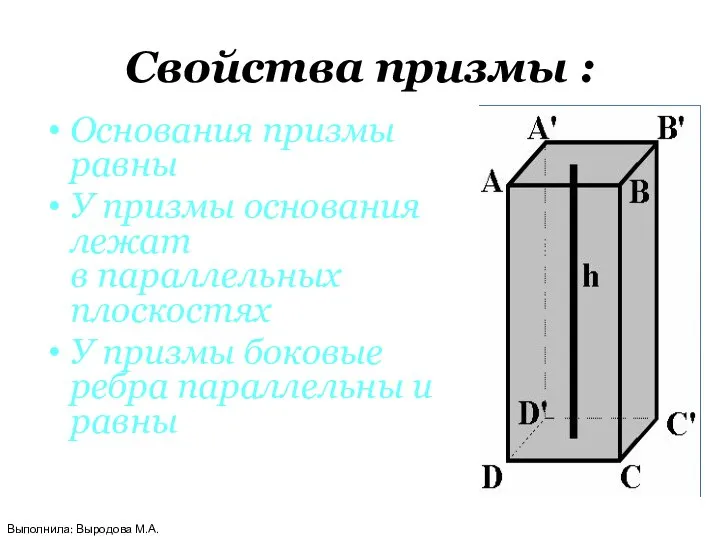
- 6. Свойства призмы : Основания призмы равны У призмы основания лежат в параллельных плоскостях У призмы боковые
- 7. Оказывается, что призма может быть не только геометрическим телом, но и художественным шедевром. Именно призма стала
- 8. Моделями прямой призмы служат : классная комната кирпич спичечный коробок Выполнила: Выродова М.А.
- 9. Городские здания чаще всего имеют форму многогранников. Как правило, это обычные параллелепипеды. И лишь неожиданные архитектурные
- 11. Скачать презентацию




 Вычисление пределов. Раскрытие неопределенностей
Вычисление пределов. Раскрытие неопределенностей Подготовка к ЕГЭ. Преобразование выражений
Подготовка к ЕГЭ. Преобразование выражений Геометрические приложения определенного интеграла
Геометрические приложения определенного интеграла Сравнение целых чисел
Сравнение целых чисел Анализ контрольной работы. Величины
Анализ контрольной работы. Величины Памятка по оформлению краткой записи к задачам. 1-2 класс
Памятка по оформлению краткой записи к задачам. 1-2 класс Односторонние пределы
Односторонние пределы Длина окружности. Площадь
Длина окружности. Площадь Презентация по математике "Свойства величин" -
Презентация по математике "Свойства величин" -  Презентация на тему Страна отрицательных чисел
Презентация на тему Страна отрицательных чисел  Механический и геометрический смысл производной
Механический и геометрический смысл производной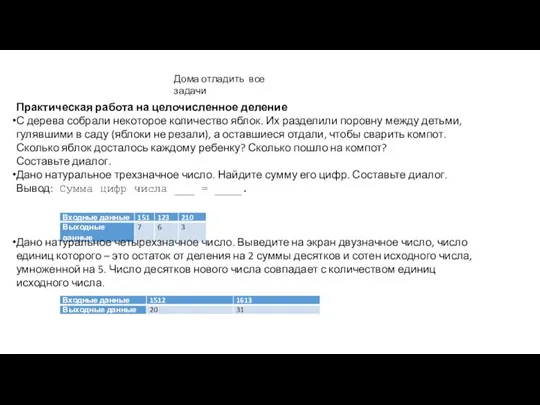 Практическая работа на целочисленное деление
Практическая работа на целочисленное деление Цифры (дойти до апельсина)
Цифры (дойти до апельсина) Как построить график функции y=f(x+l)+m из графика функции y=f(x)
Как построить график функции y=f(x+l)+m из графика функции y=f(x) Проект по математике Задачи-расчеты из моей жизни
Проект по математике Задачи-расчеты из моей жизни Презентация на тему Метод интервалов
Презентация на тему Метод интервалов  Графики функций
Графики функций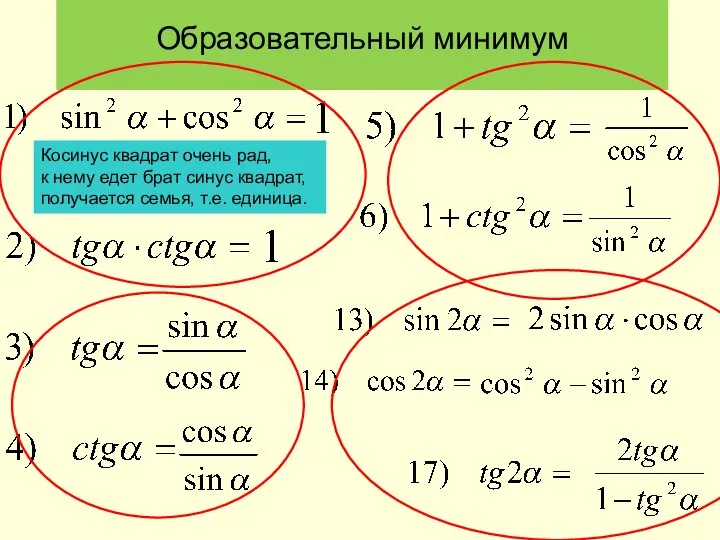 Образовательный минимум
Образовательный минимум Простейшие тригонометрические уравнения
Простейшие тригонометрические уравнения Прямоугольный треугольник. Решение задач
Прямоугольный треугольник. Решение задач Последовательность
Последовательность История счета и систем счисления
История счета и систем счисления Словарь Владимира Ивановича Даля
Словарь Владимира Ивановича Даля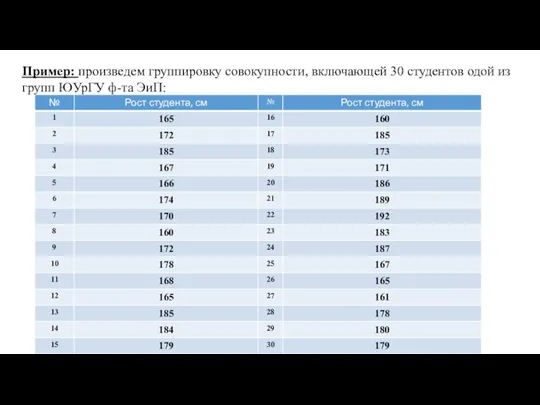 Группировка
Группировка Векторная алгебра
Векторная алгебра Цветочное настроение. Математика
Цветочное настроение. Математика Понятие теории игр
Понятие теории игр Преобразование выражений, содержащих квадратные корни
Преобразование выражений, содержащих квадратные корни