Содержание
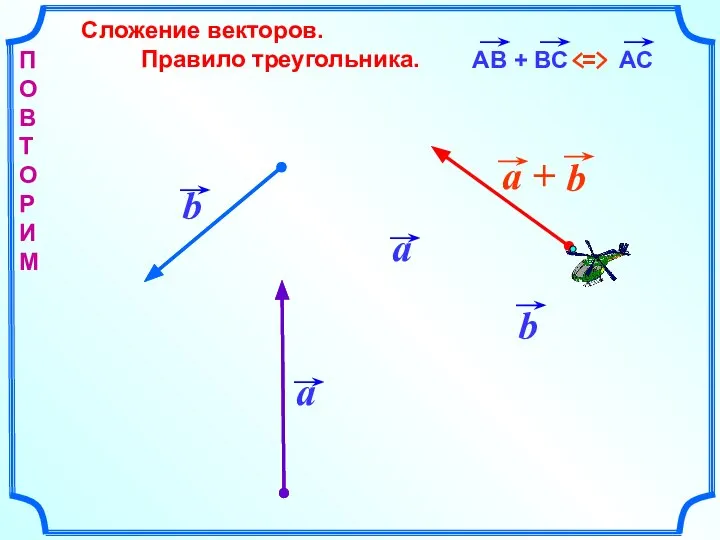
- 2. Сложение векторов. Правило треугольника. b П О В Т О Р И М
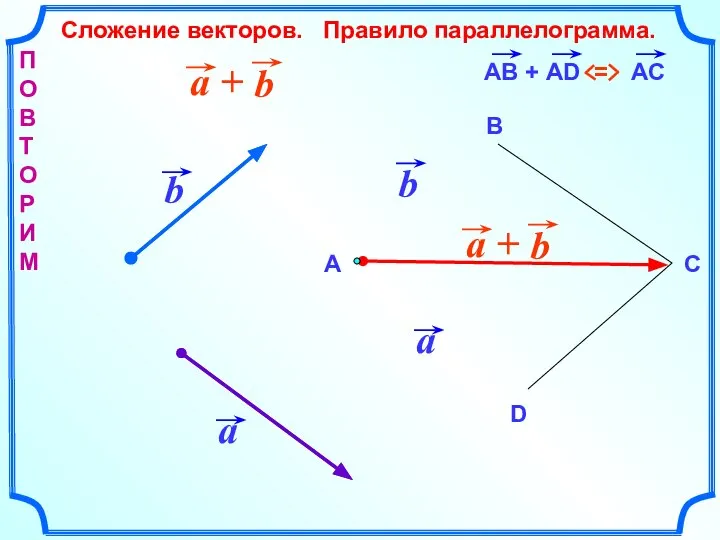
- 3. Сложение векторов. Правило параллелограмма. А В D C П О В Т О Р И М
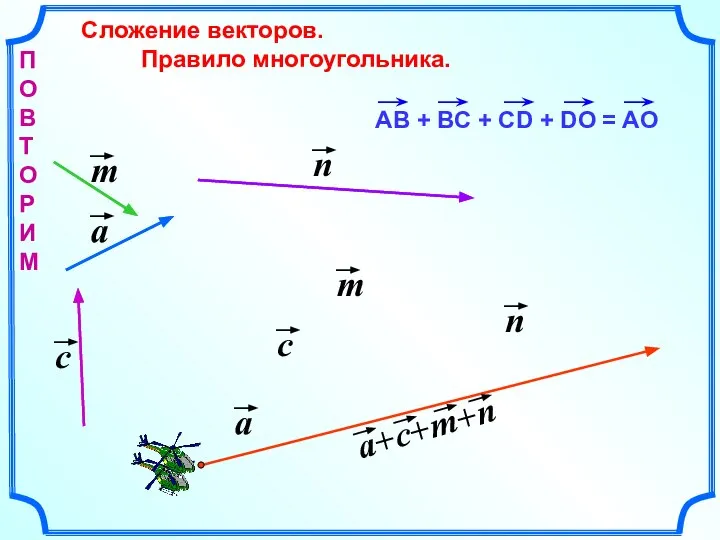
- 4. Сложение векторов. Правило многоугольника. П О В Т О Р И М
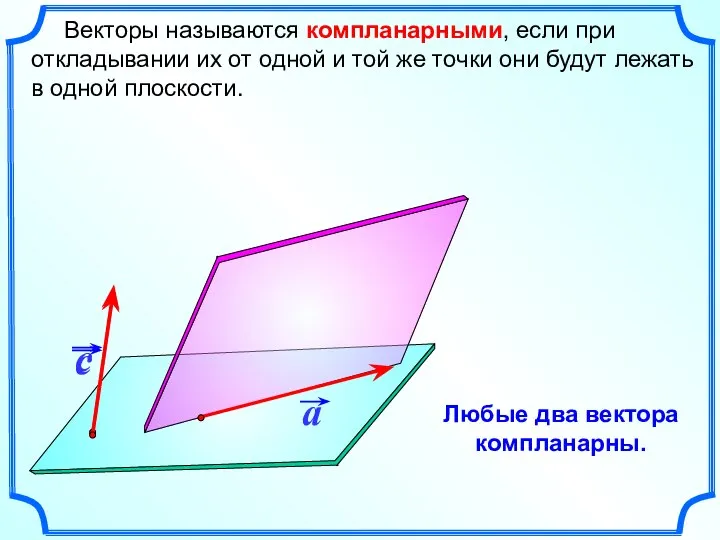
- 5. Векторы называются компланарными, если при откладывании их от одной и той же точки они будут лежать
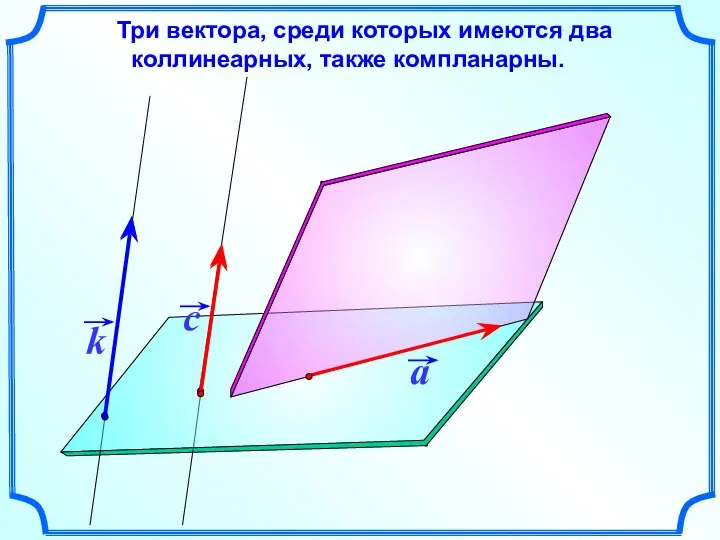
- 6. Три вектора, среди которых имеются два коллинеарных, также компланарны.
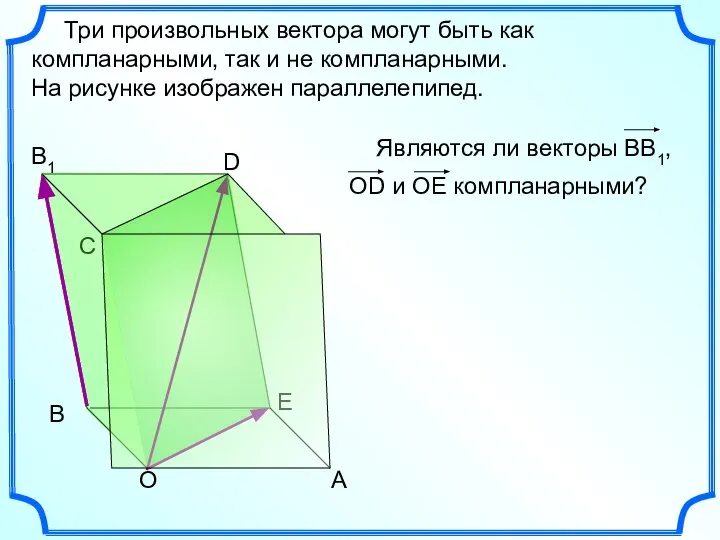
- 7. Три произвольных вектора могут быть как компланарными, так и не компланарными. На рисунке изображен параллелепипед. А
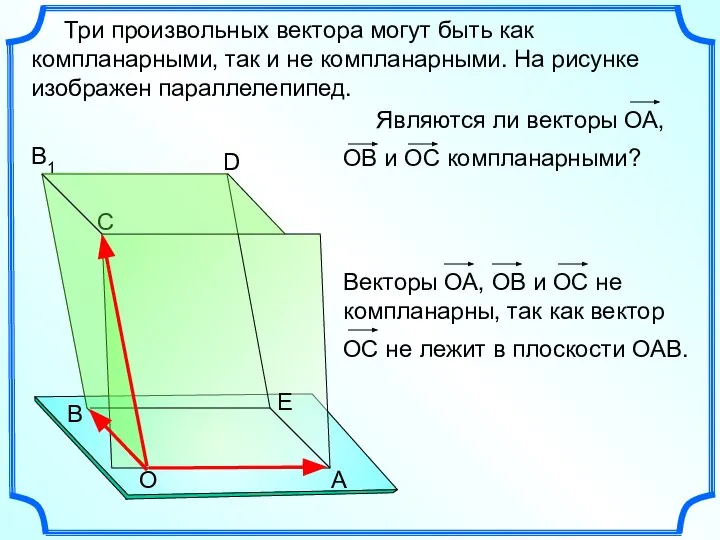
- 8. Три произвольных вектора могут быть как компланарными, так и не компланарными. На рисунке изображен параллелепипед. А
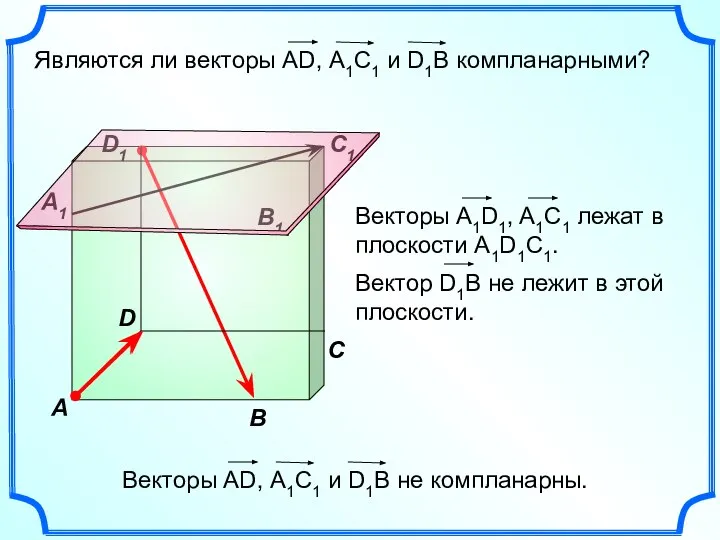
- 9. B C A1 B1 C1 D1 A D
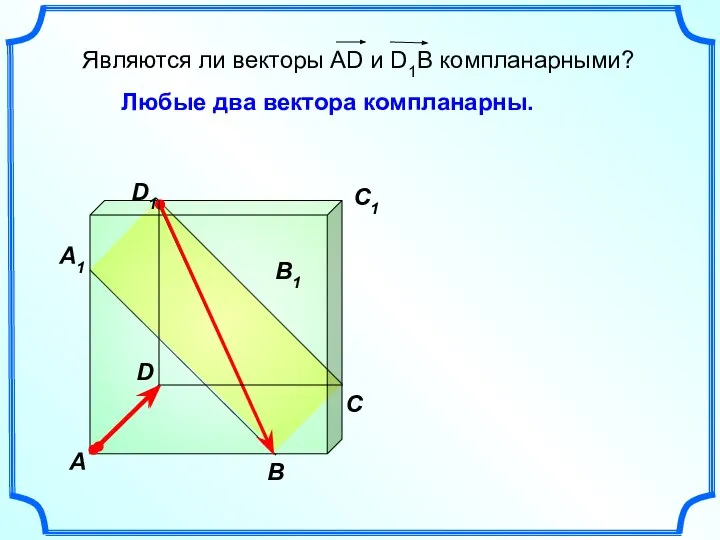
- 10. A B C A1 B1 C1 D1 D Любые два вектора компланарны.
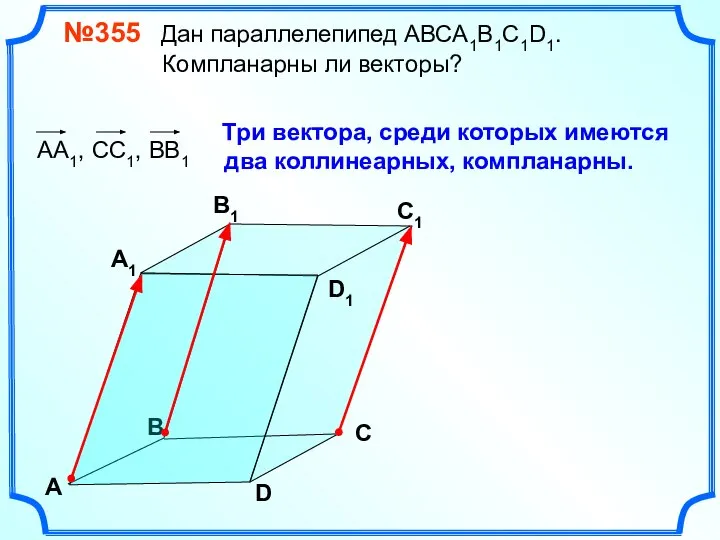
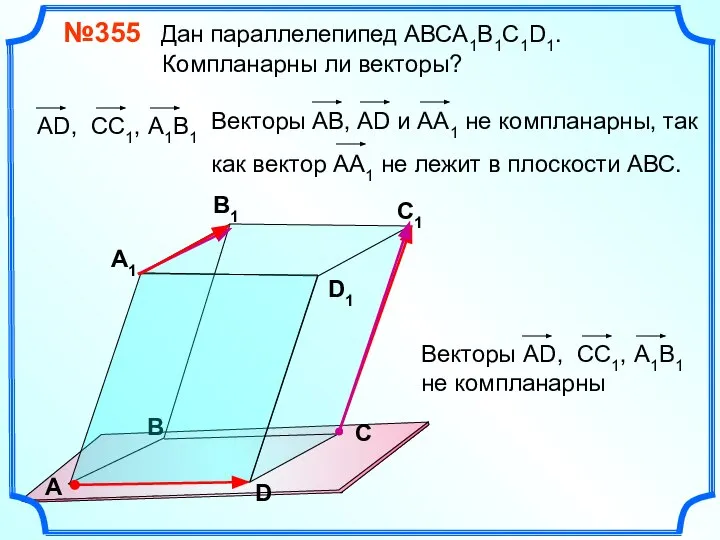
- 11. №355 Дан параллелепипед АВСA1B1C1D1. Компланарны ли векторы? В А В1 С1 D1 D С А1 Три
- 12. №355 Дан параллелепипед АВСA1B1C1D1. Компланарны ли векторы? В А В1 С1 D1 D С А1
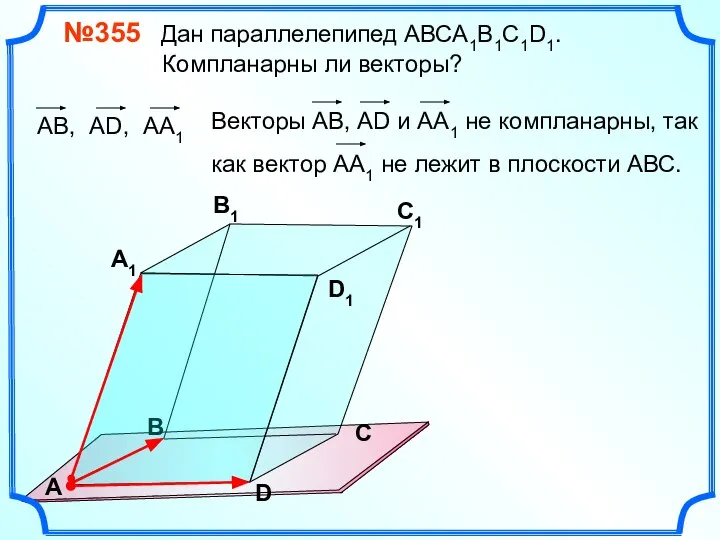
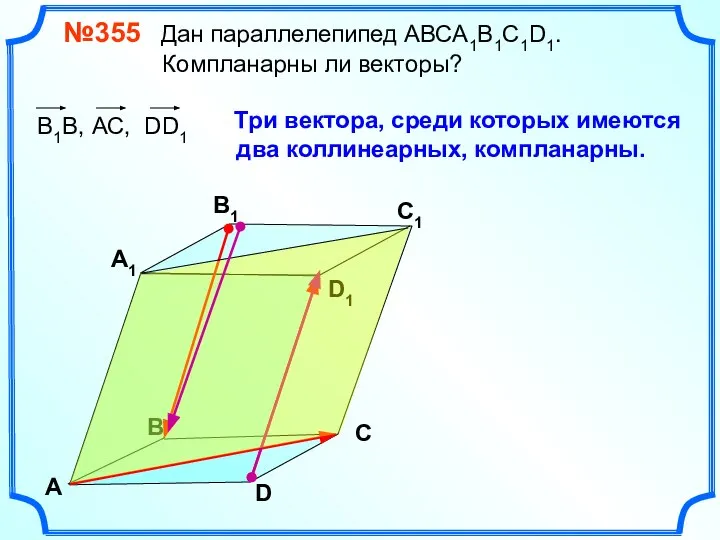
- 13. №355 Дан параллелепипед АВСA1B1C1D1. Компланарны ли векторы? В А В1 С1 D1 D С А1 Три
- 14. №355 Дан параллелепипед АВСA1B1C1D1. Компланарны ли векторы? В А В1 С1 D1 D С А1
- 15. Любые два вектора компланарны. Три вектора, среди которых имеются два коллинеарных, также компланарны. ЗАПОМНИТЬ!!!
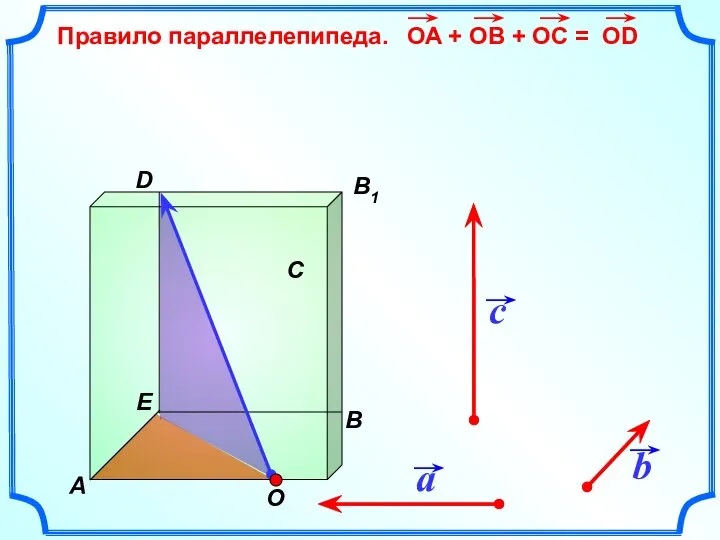
- 16. Правило параллелепипеда. b
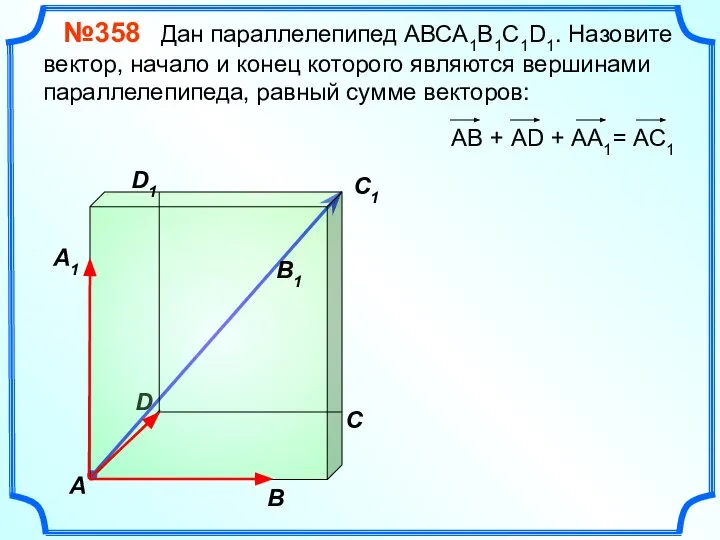
- 17. В A С B1 C1 D1 №358 Дан параллелепипед АВСA1B1C1D1. Назовите вектор, начало и конец которого
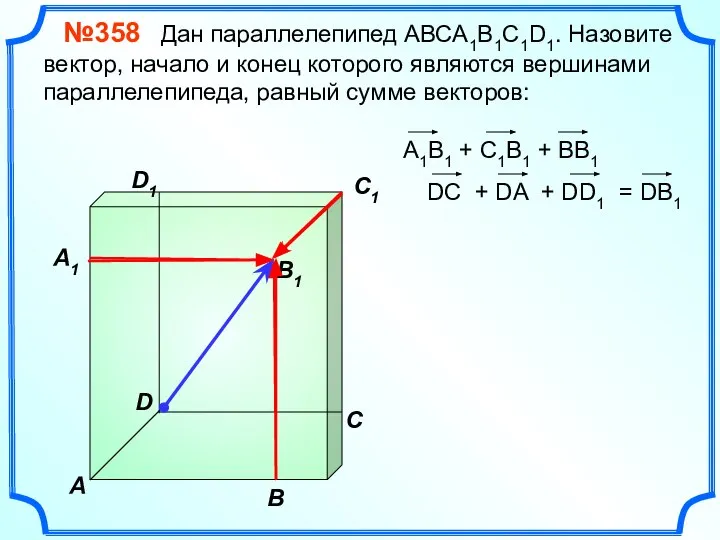
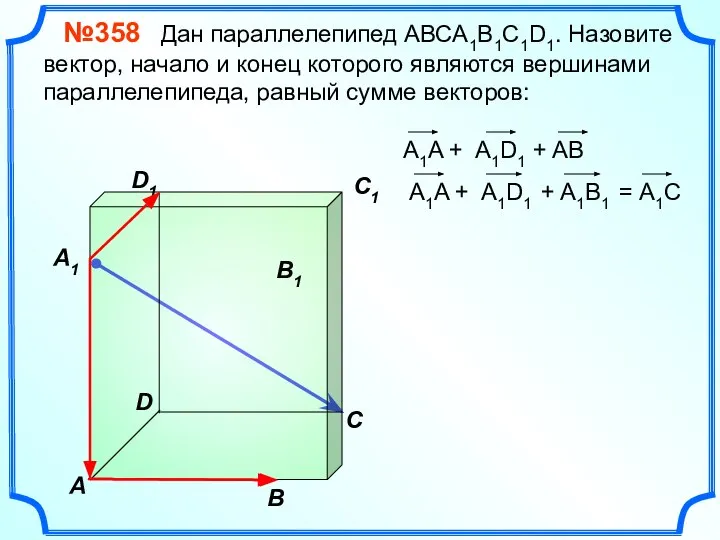
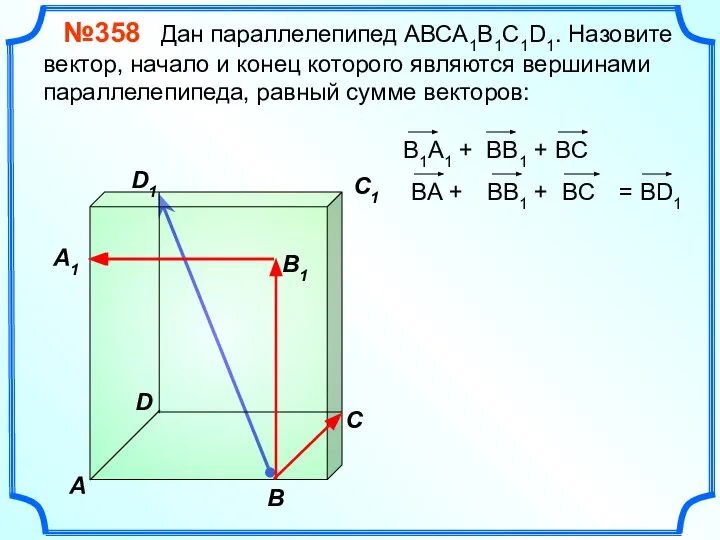
- 18. В A С C1 D1 №358 Дан параллелепипед АВСA1B1C1D1. Назовите вектор, начало и конец которого являются
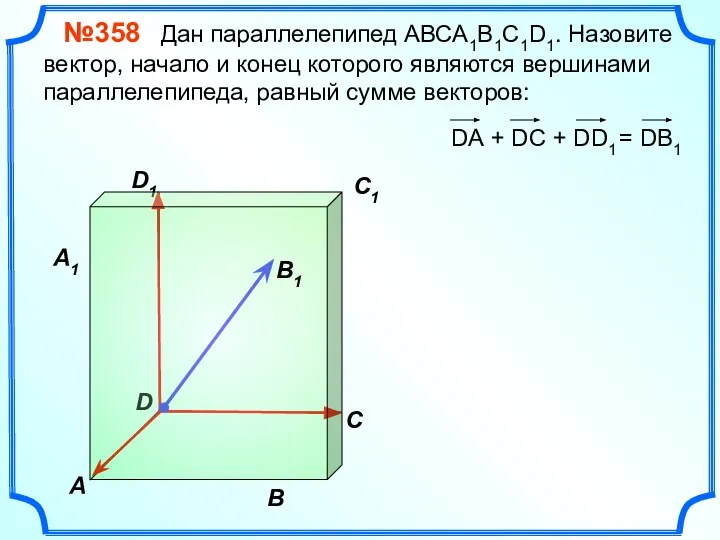
- 19. В A С C1 D1 №358 Дан параллелепипед АВСA1B1C1D1. Назовите вектор, начало и конец которого являются
- 20. В A С C1 D1 №358 Дан параллелепипед АВСA1B1C1D1. Назовите вектор, начало и конец которого являются
- 21. В A С C1 D1 №358 Дан параллелепипед АВСA1B1C1D1. Назовите вектор, начало и конец которого являются
- 22. Теорема о разложении вектора по трем некомпланарным векторам. Любой вектор можно разложить по трем данным некомпланарным
- 24. Скачать презентацию


 Анализ и изображение пространственных фигур
Анализ и изображение пространственных фигур Исследование функций
Исследование функций Скрипт параллелограм
Скрипт параллелограм Презентация на тему Параллельный перенос и Поворот
Презентация на тему Параллельный перенос и Поворот  Математик Чарльз Лютвидж Доджсон и писатель Льюис Кэрролл
Математик Чарльз Лютвидж Доджсон и писатель Льюис Кэрролл Сложение вида +6
Сложение вида +6 Письменные приемы вычислений
Письменные приемы вычислений Сказка об отрезке
Сказка об отрезке Деление десятичных дробей
Деление десятичных дробей Разложение вектора по направлениям. Скалярное произведение векторов
Разложение вектора по направлениям. Скалярное произведение векторов Особенности проведения олимпиады по математике в 2016-17 учебном году
Особенности проведения олимпиады по математике в 2016-17 учебном году Многогранники в нашей жизни
Многогранники в нашей жизни Презентация на тему Квадратичная функция и ее свойства
Презентация на тему Квадратичная функция и ее свойства  Элементы теории фредгольмовых отображений
Элементы теории фредгольмовых отображений Дроби
Дроби Сложение и вычитание в пределах первого десятка
Сложение и вычитание в пределах первого десятка Пропорция
Пропорция Таблица умножения на 2
Таблица умножения на 2 Математика ЕГЭ. Треугольники
Математика ЕГЭ. Треугольники Вопросы при решении задач
Вопросы при решении задач Автоматы и алгоритмы. Комбинационные схемы и конечные автоматы
Автоматы и алгоритмы. Комбинационные схемы и конечные автоматы Презентация на тему Приемы доказательства неравенств, содержащих переменные
Презентация на тему Приемы доказательства неравенств, содержащих переменные  Параллельные прямые
Параллельные прямые Страна геометрических фигур
Страна геометрических фигур Исследование модели многогранника с сечениями на примере куба
Исследование модели многогранника с сечениями на примере куба Выборочное наблюдение
Выборочное наблюдение Игра на поиск логических пар
Игра на поиск логических пар Действия с десятичными дробями. 5 класс
Действия с десятичными дробями. 5 класс