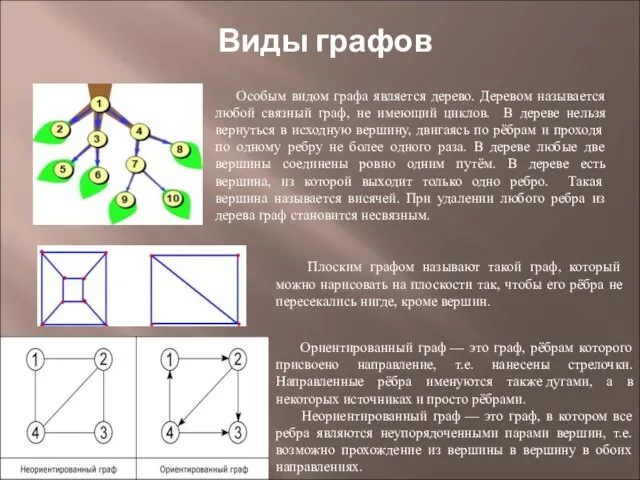
имеющий циклов. В дереве нельзя вернуться в исходную вершину, двигаясь по рёбрам и проходя по одному ребру не более одного раза. В дереве любые две вершины соединены ровно одним путём. В дереве есть вершина, из которой выходит только одно ребро. Такая вершина называется висячей. При удалении любого ребра из дерева граф становится несвязным.
Плоским графом называют такой граф, который можно нарисовать на плоскости так, чтобы его рёбра не пересекались нигде, кроме вершин.
Ориентированный граф — это граф, рёбрам которого присвоено направление, т.е. нанесены стрелочки. Направленные рёбра именуются также дугами, а в некоторых источниках и просто рёбрами.
Неориентированный граф — это граф, в котором все ребра являются неупорядоченными парами вершин, т.е. возможно прохождение из вершины в вершину в обоих направлениях.
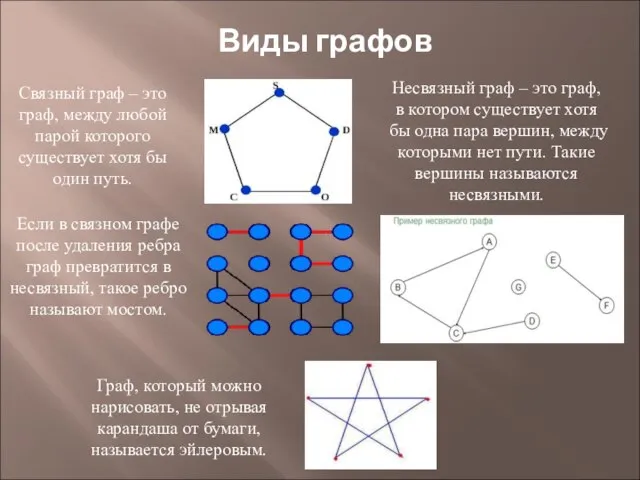
Виды графов



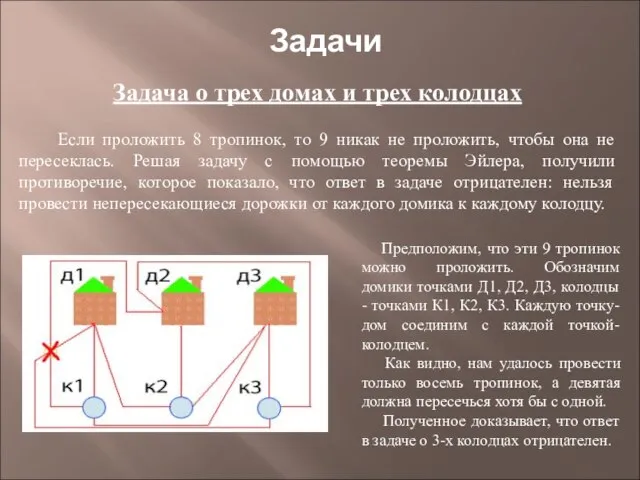
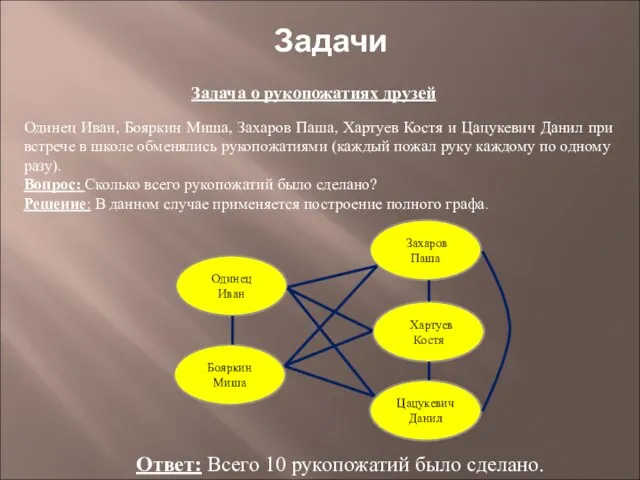



 Презентация на тему Разложение многочленов на множители
Презентация на тему Разложение многочленов на множители  Таблицы. Геометрия
Таблицы. Геометрия Азбука
Азбука Интегрирование вещественных функций по неотрицательной мере
Интегрирование вещественных функций по неотрицательной мере Движение. Виды движения
Движение. Виды движения Разделите выражения на группы
Разделите выражения на группы Метрологические понятия
Метрологические понятия Одночлены и их свойства
Одночлены и их свойства Презентация на тему Модуль числа (6 класс)
Презентация на тему Модуль числа (6 класс)  Среднее арифметическое
Среднее арифметическое ЛЕКЦИЯ_6
ЛЕКЦИЯ_6 Функция у=log ах, ее свойства и график
Функция у=log ах, ее свойства и график Презентация по математике "Мы рады привествовать вас на уроке математики" -
Презентация по математике "Мы рады привествовать вас на уроке математики" -  Арифметическая прогрессия
Арифметическая прогрессия Тема Функция у = ах2 и её график
Тема Функция у = ах2 и её график English System of Measures
English System of Measures 1 замечательный предел
1 замечательный предел Теорема Пифагора
Теорема Пифагора Один - много. 1 класс
Один - много. 1 класс Устный счёт. Вверху, внизу,слева, справа (1 класс)
Устный счёт. Вверху, внизу,слева, справа (1 класс) Как может математика помочь быть здоровым?
Как может математика помочь быть здоровым? Квадратные уравнения
Квадратные уравнения Решение задач. Подготовка к умножению
Решение задач. Подготовка к умножению Параллелепипед. Виды параллелепипедов
Параллелепипед. Виды параллелепипедов Проценты
Проценты Системы линейных алгебраических уравнений. Лекция 1
Системы линейных алгебраических уравнений. Лекция 1 Компьютерное решение задач по теме Арифметическая прогрессия
Компьютерное решение задач по теме Арифметическая прогрессия Лекция+1+-+Предел+числовой+последовательности
Лекция+1+-+Предел+числовой+последовательности