Содержание
- 2. (1) где u(t) искомая, а h(t)-заданная функции. Линейный оператор K(t) и функции u(t), h(t) определены на
- 3. - Гильбертово пространство на [0,T] и определим норму (3)
- 4. (4)
- 5. (5) (6)
- 6. (7) (8) Тогда при каждом n задача (5) и (6) имеет единственное решение последовательности сходится в
- 7. Теорема 2. Пусть выполнены условия теоремы 1, тогда верна оценка
- 9. Скачать презентацию

![- Гильбертово пространство на [0,T] и определим норму (3)](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/848408/slide-2.jpg)




 Понятие функции
Понятие функции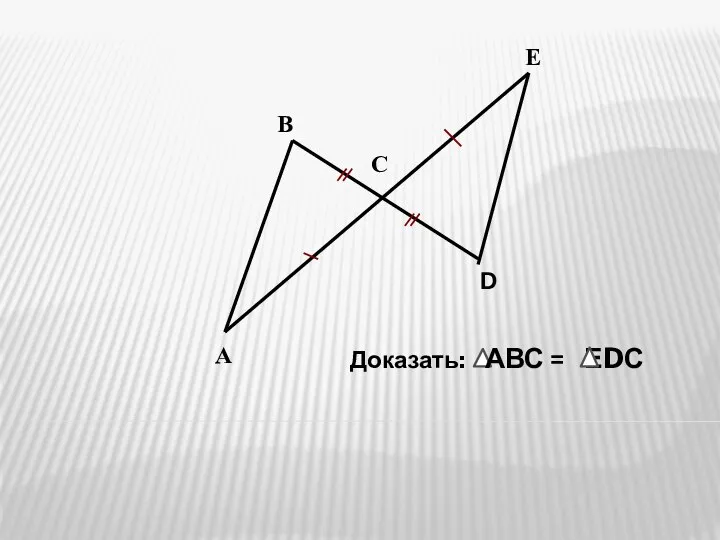 Признаки равенства треугольников. Решение задач
Признаки равенства треугольников. Решение задач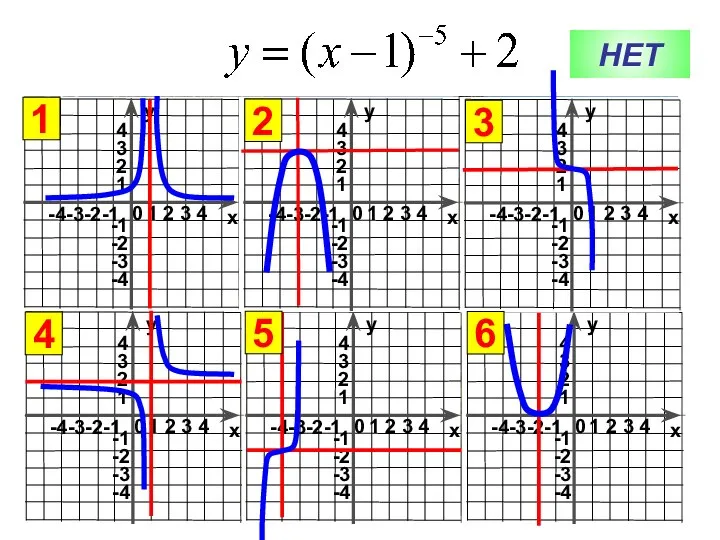 графики функций. Ошибка
графики функций. Ошибка Методы решения Слау. Метод Гаусса
Методы решения Слау. Метод Гаусса Variācijas, permutācijas, kombinācijas
Variācijas, permutācijas, kombinācijas Задачи на разрезание и перекраивание фигур
Задачи на разрезание и перекраивание фигур Презентация на тему Действия с векторами
Презентация на тему Действия с векторами  Приложение производной
Приложение производной Вычитание числа 2 (1 класс)
Вычитание числа 2 (1 класс) Допуски линейных размеров. Квалитет
Допуски линейных размеров. Квалитет Симметрия в природе
Симметрия в природе Решение задач на применение свойств прямоугольного треугольника. 7 класс
Решение задач на применение свойств прямоугольного треугольника. 7 класс Числовой коэффициент
Числовой коэффициент Квадратные уравнения. Устная разминка
Квадратные уравнения. Устная разминка Формула Стирлинга
Формула Стирлинга Старинные единицы измерения. Меры и массы и объемы
Старинные единицы измерения. Меры и массы и объемы Тригонометрические уравнения
Тригонометрические уравнения Сравнение двух прогрессий
Сравнение двух прогрессий Математика. Составные высказывания
Математика. Составные высказывания Множества точек на координатной плоскости, расстояние между точками координатной прямой
Множества точек на координатной плоскости, расстояние между точками координатной прямой Некоторые понятия о статистике, статистическом методе и термодинамике
Некоторые понятия о статистике, статистическом методе и термодинамике Математическая викторина (начальная школа)
Математическая викторина (начальная школа) Координатный луч
Координатный луч Векторы плоскости
Векторы плоскости Обыкновенные дроби. 5 класс
Обыкновенные дроби. 5 класс Площади четырёхугольников. Решение задач
Площади четырёхугольников. Решение задач Математика и физика здоровья
Математика и физика здоровья Решение задач на нахождение неизвестного вычитаемого
Решение задач на нахождение неизвестного вычитаемого