Пересечение двух поверхностей. Построение пересечения двух кривых поверхностей методом плоских посредников
Содержание
- 2. Построение линии пересечения двух поверхностей. Одна из поверхностей проецирующая Если одна из поверхностей является проецирующей, т.е.
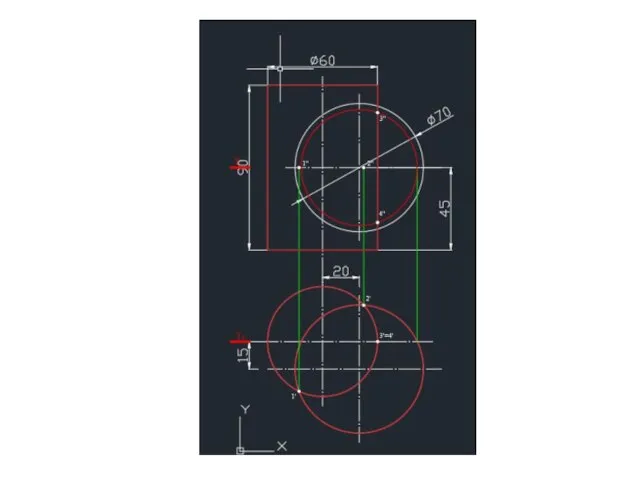
- 3. Построение линии пересечения цилиндра и сферы 1. В пересечении участвуют кривые поверхности, поэтому результат пересечения –
- 4. Построение линии пересечения цилиндра и сферы 3. Для нахождения точек могут быть использованы как горизонтальные, так
- 5. Построение линии пересечения цилиндра и сферы При использовании фронтальных плоскостей-посредников в сечениях цилиндра получаются прямоугольники; в
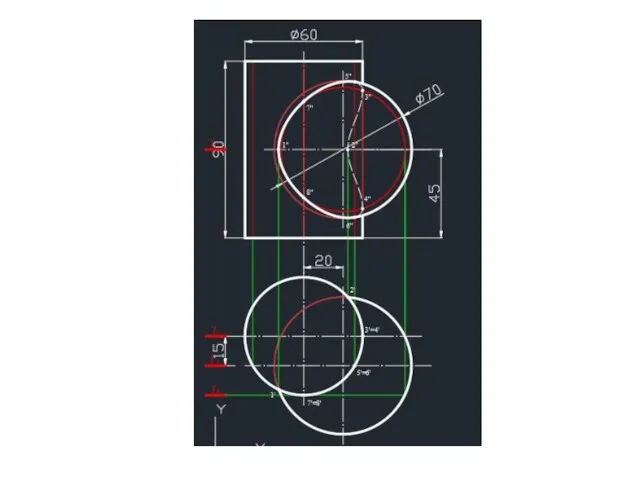
- 6. Построение линии пересечения цилиндра и сферы Для нахождения точек линии пересечения тел преимущество имеет использование фронтальных
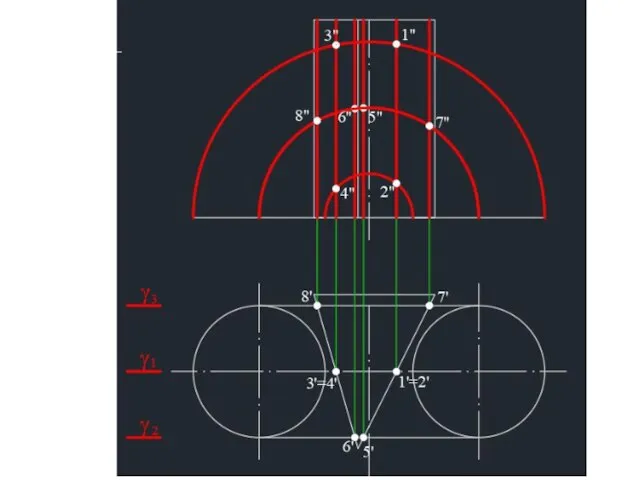
- 7. Построение линии пересечения цилиндра и сферы Горизонтальная плоскость γ1 введена для нахождения точек, принадлежащих горизонтальному очерку
- 9. Построение линии пересечения цилиндра и сферы 4. Фронтальная плоскость γ2 введена для нахождения точек, принадлежащих фронтальному
- 11. Построение линии пересечения призмы и тора 1. В пересечении участвуют кривая поверхность и гранное тело, поэтому
- 12. Построение линии пересечения призмы и тора 2. Боковые ребра призмы перпендикулярны горизонтальной плоскости проекций. Поэтому она
- 13. Построение линии пересечения призмы и тора 2. Ось вращения тора перпендикулярна фронтальной плоскости проекций. Поэтому в
- 14. Построение линии пересечения призмы и тора Фронтальные плоскости пересекают тор по окружностям, а призму – по
- 15. Построение линии пересечения призмы и тора Искомые точки для построения линии пересечения находятся в пересечении сечений
- 16. Построение линии пересечения призмы и тора 3. Фронтальная плоскость γ1 введена для нахождения точек, принадлежащих фронтальному
- 18. Построение линии пересечения призмы и тора Фронтальные плоскости γ4 и γ5 введены для нахождения промежуточных точек.
- 19. Построение линии пересечения призмы и тора Дальние ребра призмы, находящиеся за тором существуют, но не видны
- 21. Скачать презентацию















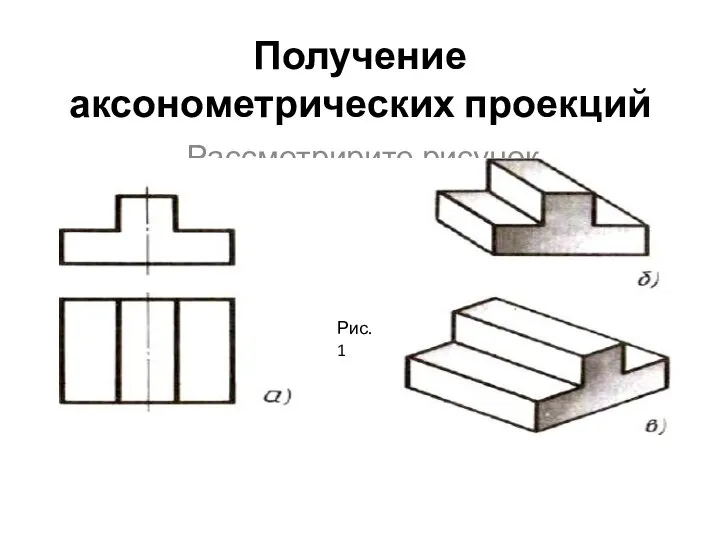 Получение аксонометрических проекций
Получение аксонометрических проекций Тригонометрические уравнения. Методы решения тригонометрических уравнений
Тригонометрические уравнения. Методы решения тригонометрических уравнений Решение задач по теме: Терема Пифагора
Решение задач по теме: Терема Пифагора Презентация на тему Подобные треугольники
Презентация на тему Подобные треугольники  Логика. Логические функции
Логика. Логические функции Наши проекты. Оригами Странички для любознательных
Наши проекты. Оригами Странички для любознательных Квадратичная функция и её график
Квадратичная функция и её график Решение одной задачи, не лишено здравого смысла
Решение одной задачи, не лишено здравого смысла Аттестационная работа. Взаимодействие учебной и исследовательской деятельности на уроках математики
Аттестационная работа. Взаимодействие учебной и исследовательской деятельности на уроках математики Координатная плоскость
Координатная плоскость Арксинус, арккосинус, арктангенс, арккотангенс
Арксинус, арккосинус, арктангенс, арккотангенс Декартовы координаты на плоскости (решение задач)
Декартовы координаты на плоскости (решение задач) Способы задания числовых функций
Способы задания числовых функций Роль геометрии в изобразительном искусстве
Роль геометрии в изобразительном искусстве Движение: скорость, время, расстояние
Движение: скорость, время, расстояние Функция y = x2 и её график
Функция y = x2 и её график Неопределенный интеграл
Неопределенный интеграл Диалектика как методология научного познания
Диалектика как методология научного познания Треугольник и его виды
Треугольник и его виды Порядок действий в выражениях
Порядок действий в выражениях Решение задач по теме Параллельность прямой и плоскости
Решение задач по теме Параллельность прямой и плоскости Презентация на тему Тренажер - Табличное умножение и деление
Презентация на тему Тренажер - Табличное умножение и деление  Построение аксонометрических проекций геометрических фигур и тел
Построение аксонометрических проекций геометрических фигур и тел Дифференциальные уравнения
Дифференциальные уравнения Система линейных уравнений
Система линейных уравнений Цилиндр
Цилиндр Математическое моделирование. Воспроизводимость опытов
Математическое моделирование. Воспроизводимость опытов Интерактивные Крестики-нолики. Решение квадратных уравнений
Интерактивные Крестики-нолики. Решение квадратных уравнений