Содержание
- 2. СОДЕЖАНИЕ 2
- 3. ВВЕДЕНИЕ «Геометрия владеет двумя сокровищами: одно из них – это теорема Пифагора, а другое – деление
- 4. ЦЕЛЬ ПРОЕКТА Познание математических закономерностей в мире, определение значения математики в мировой культуре и дополнение системы
- 5. ИСТОРИЯ «ЗОЛОТОГО СЕЧЕНИЯ» В Древнем Египте существовала «система правил гармонии», основанная на Золотом Сечении. В Древней
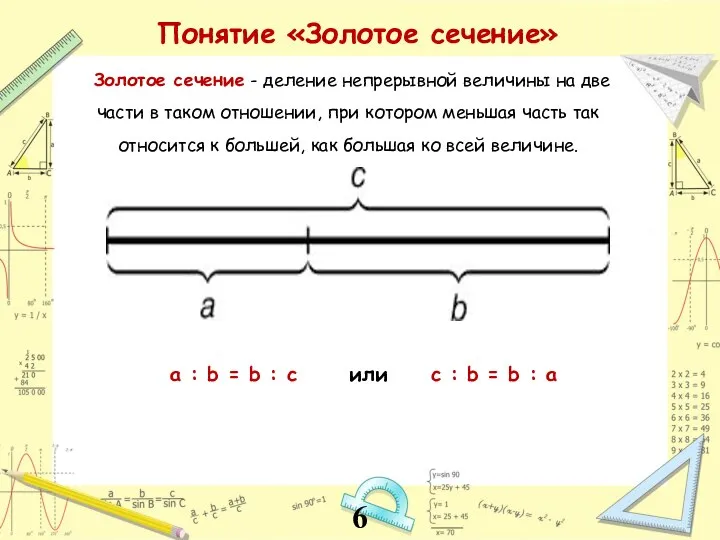
- 6. Понятие «Золотое сечение» Золотое сечение - деление непрерывной величины на две части в таком отношении, при
- 7. Эта пропорция равна: Золотое сечение в процентах 7
- 8. Число j является положительным корнем квадратного уравнения: x2 = x + 1 подставим корень j вместо
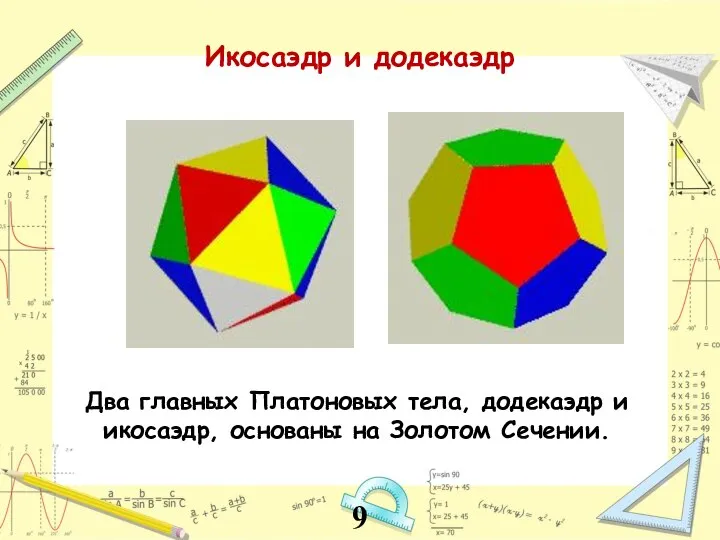
- 9. Два главных Платоновых тела, додекаэдр и икосаэдр, основаны на Золотом Сечении. Икосаэдр и додекаэдр 9
- 10. Ряд Фибоначчи С историей золотого сечения связано имя итальянского математика Леонардо Фибоначчи. Ряд чисел 0, 1,
- 11. «Золотая Пропорция» - главный эстетический принцип эпохи Средневековья Эпоха Возрождения ассоциируется с именами таких «титанов», как
- 12. Вклад Кеплера в теорию Золотого Сечения Гениальный астроном Иоганн Кеплер (1571-1630) был последовательным приверженцем Золотого Сечения,
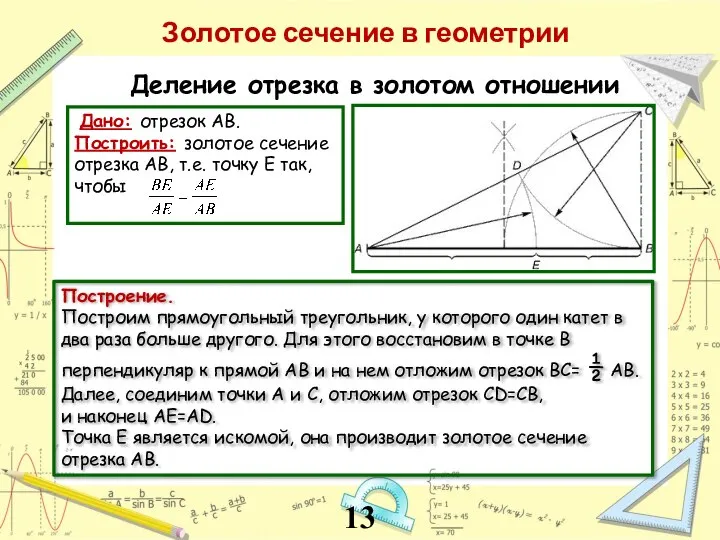
- 13. Дано: отрезок АВ. Построить: золотое сечение отрезка АВ, т.е. точку Е так, чтобы Построение. Построим прямоугольный
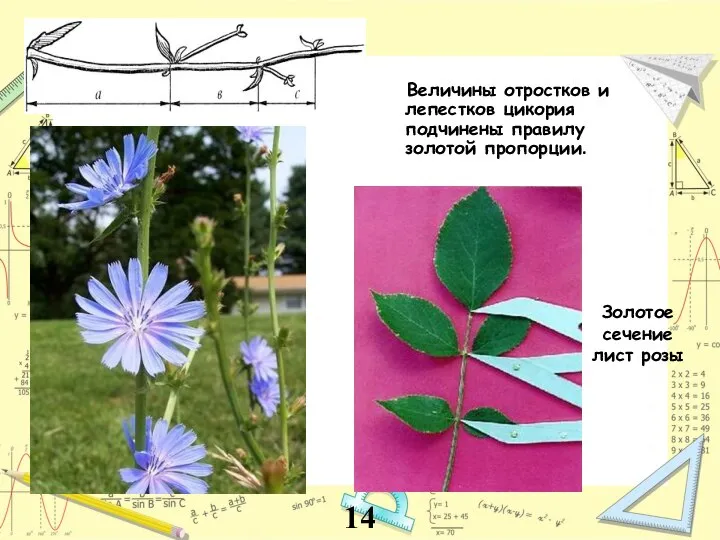
- 14. Золотое сечение лист розы Величины отростков и лепестков цикория подчинены правилу золотой пропорции. 14
- 15. Золотая пропорция в теле ящерицы – длина хвоста так относится к длине остального тела, как 62
- 16. У многих бабочек узоры на крыльях, соотношение размеров грудной и брюшной части тела соответствуют золотой пропорции
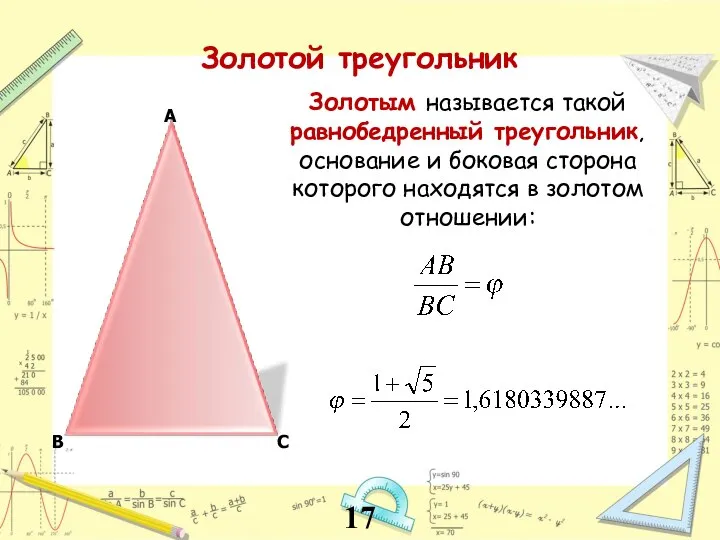
- 17. А В С Золотым называется такой равнобедренный треугольник, основание и боковая сторона которого находятся в золотом
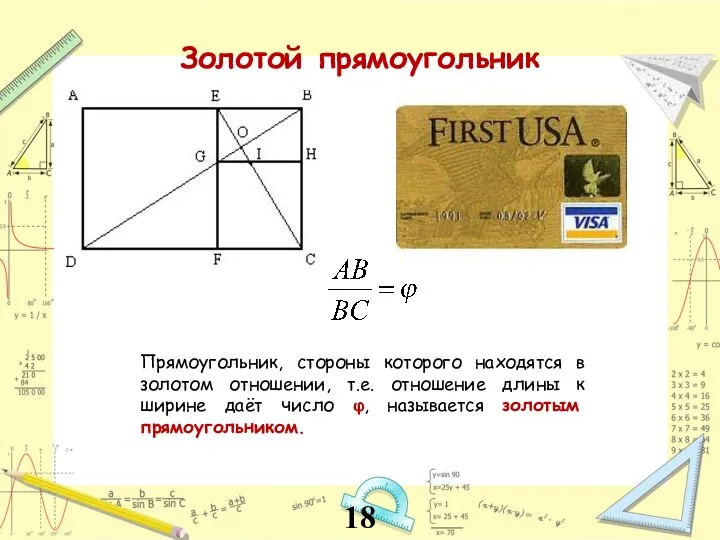
- 18. Прямоугольник, стороны которого находятся в золотом отношении, т.е. отношение длины к ширине даёт число φ, называется
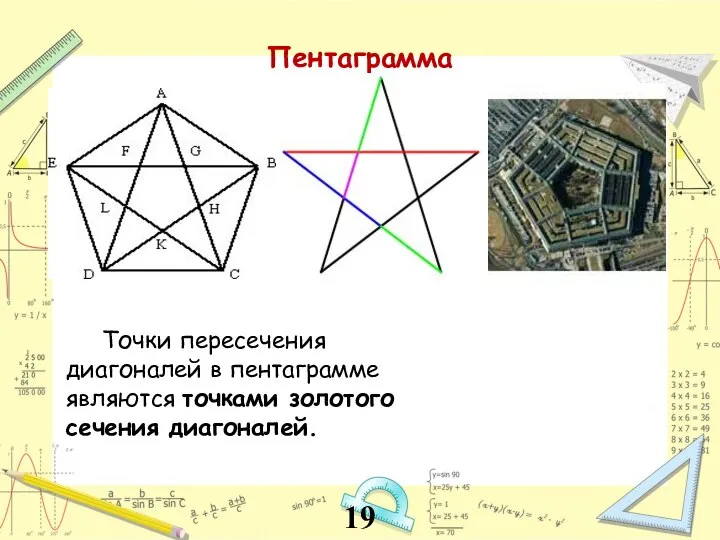
- 19. Пентаграмма Точки пересечения диагоналей в пентаграмме являются точками золотого сечения диагоналей. 19
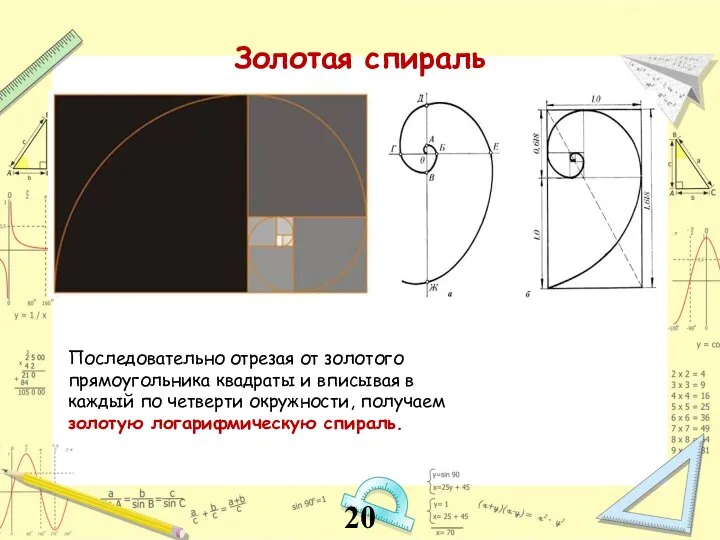
- 20. Последовательно отрезая от золотого прямоугольника квадраты и вписывая в каждый по четверти окружности, получаем золотую логарифмическую
- 21. Золотое сечение в природе Гете называл спираль "кривой жизни". Спираль увидели в расположении семян подсолнечника, в
- 22. 22
- 23. Цветки и семена подсолнуха, ромашки, чешуйки в плодах ананаса, хвойных шишках "упакованы" по логарифмическим ("золотым") спиралям,
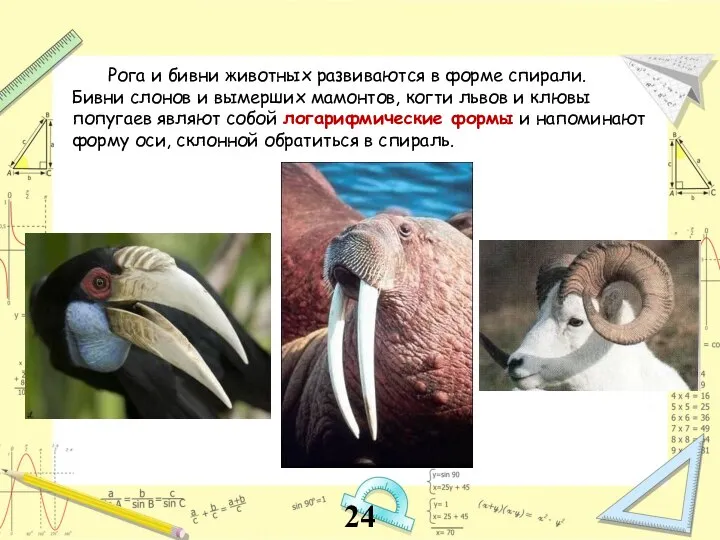
- 24. Рога и бивни животных развиваются в форме спирали. Бивни слонов и вымерших мамонтов, когти львов и
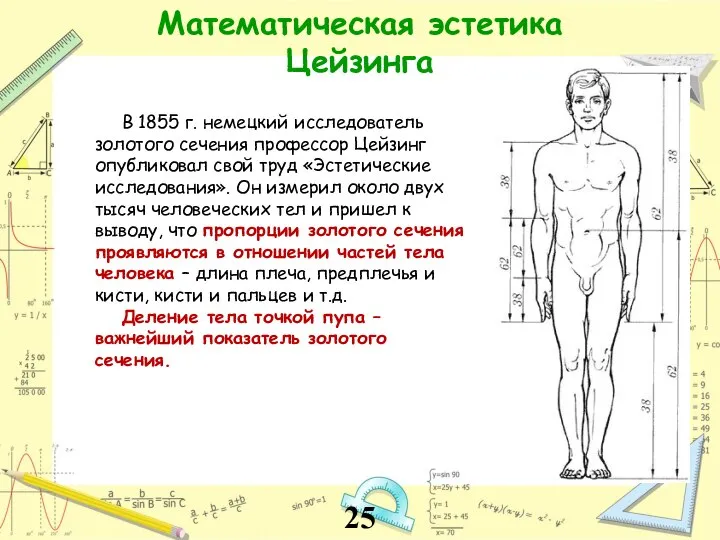
- 25. Математическая эстетика Цейзинга В 1855 г. немецкий исследователь золотого сечения профессор Цейзинг опубликовал свой труд «Эстетические
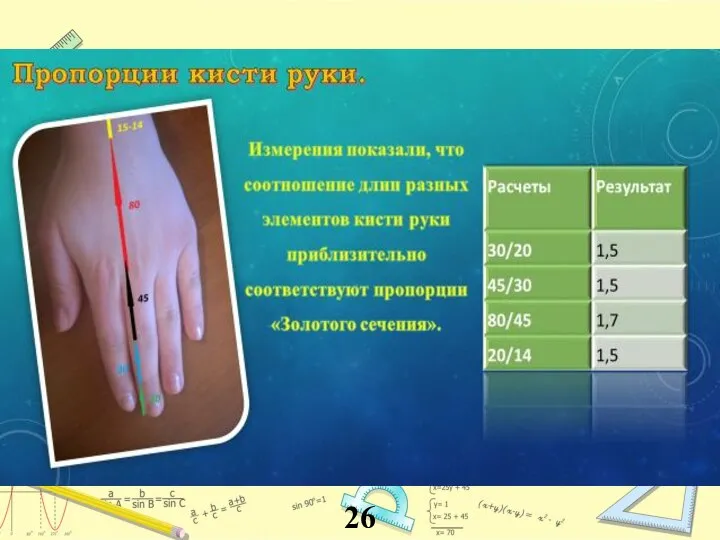
- 26. 26
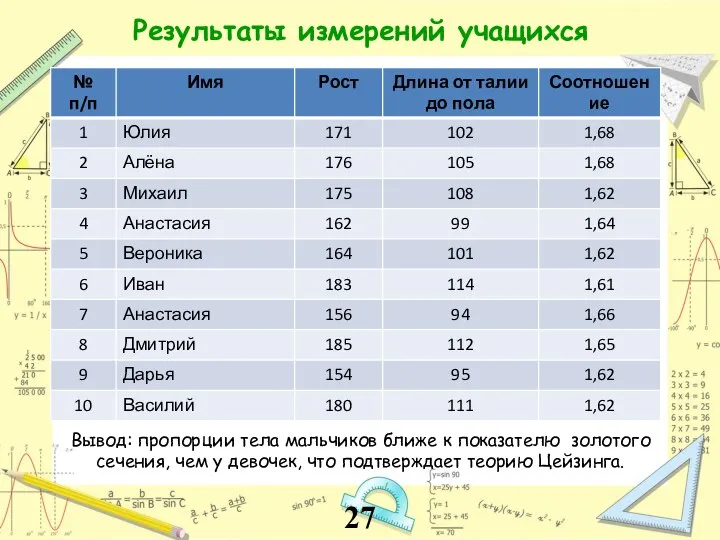
- 27. Результаты измерений учащихся Вывод: пропорции тела мальчиков ближе к показателю золотого сечения, чем у девочек, что
- 28. Математические закономерности русских мер 28
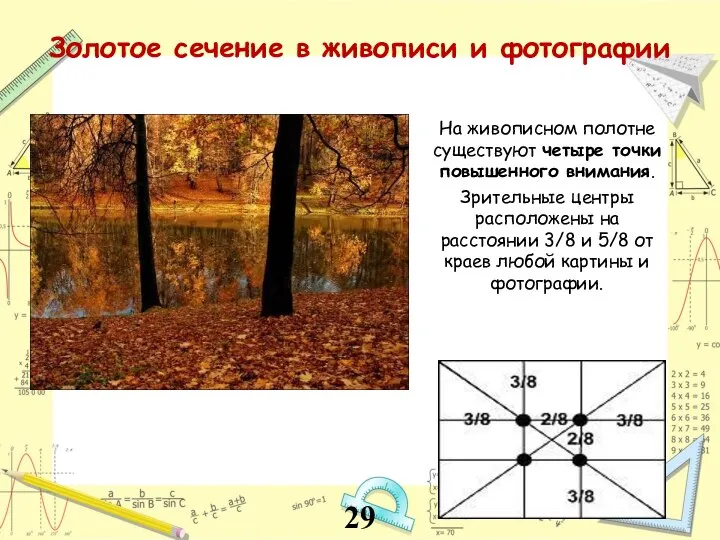
- 29. Золотое сечение в живописи и фотографии На живописном полотне существуют четыре точки повышенного внимания. Зрительные центры
- 30. Золотое сечение в скульптуре Венера Милосская Дорифор Поликлета 30
- 31. Золотое сечение в картине Леонардо да Винчи "Джоконда" Портрет Моны Лизы привлекает тем, что композиция рисунка
- 32. Васильев «У окна» «Суд Париса» камея Иванов «Явление Христа народу» «Поющий Один» 8 век 32
- 33. Золотое сечение в архитектуре Пропорции пирамиды Хеопса, храмов, барельефов, предметов быта и украшений из гробницы Тутанхамона
- 34. Золотые пропорции Парфенона 34
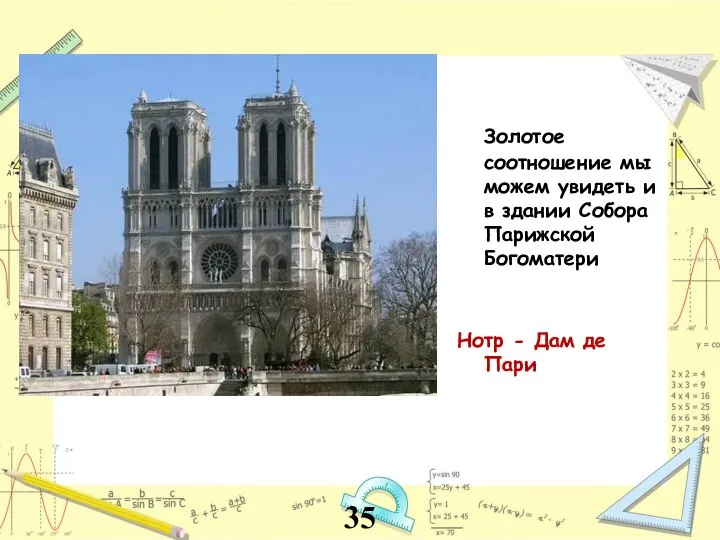
- 35. Золотое соотношение мы можем увидеть и в здании Собора Парижской Богоматери Нотр - Дам де Пари
- 36. Золотое сечение в архитектуре России Собор Христа Спасителя 36
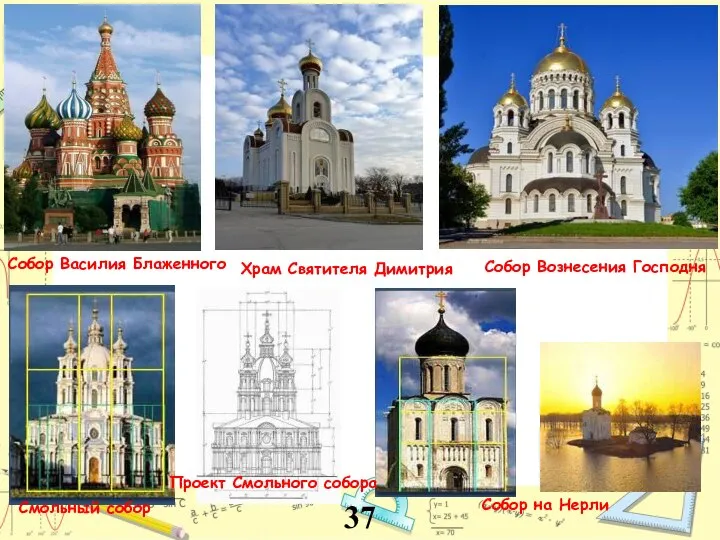
- 37. Собор на Нерли Смольный собор Собор Вознесения Господня Проект Смольного собора Собор Василия Блаженного Храм Святителя
- 38. Угловая Арсенальная башня Ещё в 6 классе, решая одну из задач, я рассмотрела фотографию Угловой Арсенальной
- 39. Тайницкая башня В этой же задаче, рассмотрев Тайницкую башню, пришла к выводу, что ВС/АВ=5/8=0,6…, а так
- 40. ВЫВОД Не одно столетие ученые применяют уникальные математические свойства золотого сечения. Универсальность его проявления в строении
- 41. ЛИТЕРАТУРА: Геометрия: красота и гармония. Простейшие задачи аналитической геометрии на плоскости. Золотая пропорция. Симметрия вокруг нас.
- 43. Скачать презентацию

























 Окружность и круг
Окружность и круг Решение задач с помощью уравнений. Алгебра. 7 класс. Ю.М. Колягин и др
Решение задач с помощью уравнений. Алгебра. 7 класс. Ю.М. Колягин и др Матрицы и определители
Матрицы и определители Первое знакомство с понятием вероятность. Урок 146
Первое знакомство с понятием вероятность. Урок 146 Презентация на тему Умножаем и делим на 10, 100, 1000 (3 класс)
Презентация на тему Умножаем и делим на 10, 100, 1000 (3 класс)  Проценты. Задачи на концентрацию, сплавы. ЕГЭ В11
Проценты. Задачи на концентрацию, сплавы. ЕГЭ В11 Решение задач по теме Теорема Пифагора и площади фигур. 8 класс
Решение задач по теме Теорема Пифагора и площади фигур. 8 класс L_3
L_3 Неопределенные интегралы
Неопределенные интегралы Самостоятельная работа по математике
Самостоятельная работа по математике Прямоугольная система координат в пространстве
Прямоугольная система координат в пространстве Методы решения логических задач
Методы решения логических задач Целое уравнение
Целое уравнение Презентация на тему Умножение двузначного числа на однозначное (3 класс)
Презентация на тему Умножение двузначного числа на однозначное (3 класс)  Градусное измерение углов. Сумма углов в треугольнике. Тест
Градусное измерение углов. Сумма углов в треугольнике. Тест dispersionnyy-analiz(1)
dispersionnyy-analiz(1) Прямая и плоскость в пространстве. Лекция 6
Прямая и плоскость в пространстве. Лекция 6 Многоугольники в жизни
Многоугольники в жизни парні і непарні функції-1
парні і непарні функції-1 Сантиметр - единица измерения длины
Сантиметр - единица измерения длины Факториал
Факториал ОГЭ 2020-21. Задание №9. Найдите корень уравнения
ОГЭ 2020-21. Задание №9. Найдите корень уравнения Ряды
Ряды Правильные многоугольники
Правильные многоугольники Граница круга
Граница круга Теорема Пифагора
Теорема Пифагора Сравнение выражений
Сравнение выражений Презентация на тему Транспортир. Измерение углов транспортиром
Презентация на тему Транспортир. Измерение углов транспортиром