Содержание
- 2. Объединением множеств A и B называется множество A∪B, все элементы которого являются элементами множества A или
- 3. Относительным дополнением множества A до множества X называется множество X\A всех тех элементов множества X, которые
- 4. Диаграммы Эйлера Первым стал использовать теперь общепринятые обозначения операций над множествами Джузеппе Пеано (1888 г.).
- 5. Для наглядного представления отношений между подмножествами какого-либо универсума используются диаграммы Эйлера. В этом случае множества обозначают
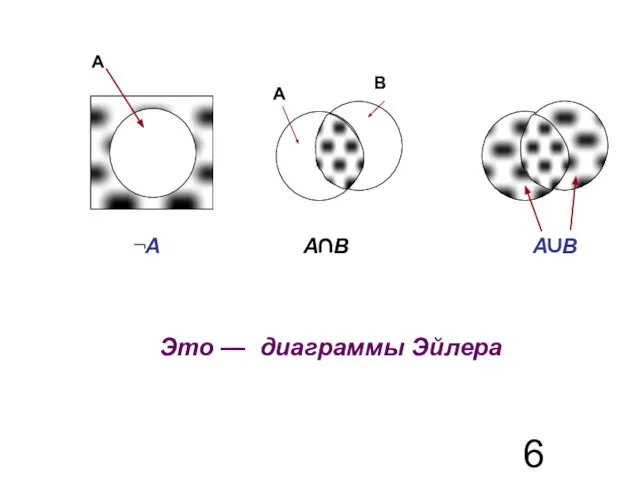
- 6. ¬A A∩B A∪B А А В Это — диаграммы Эйлера
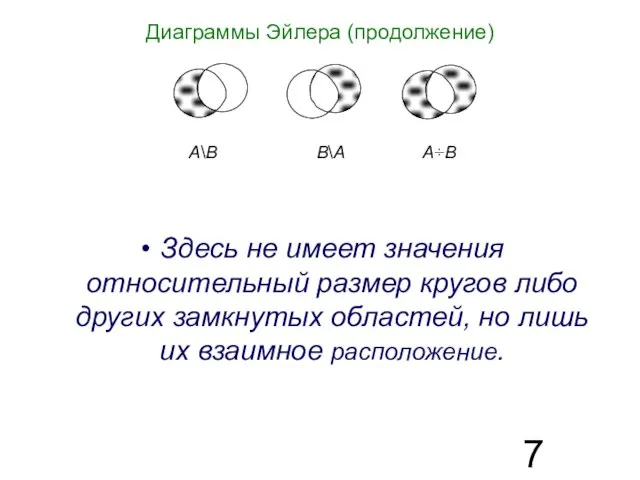
- 7. Диаграммы Эйлера (продолжение) Здесь не имеет значения относительный размер кругов либо других замкнутых областей, но лишь
- 8. Такие диаграммы могут играть в логике лишь ту роль, что чертежи в геометрии: они иллюстрируют, помогают
- 9. Булевы тождества
- 10. Джордж Буль Джордж Буль (англ.George Boole; 2 ноября 1815, Линкольн — 8 декабря 1864, Баллинтемпл, графство
- 11. Теорема 4. Для любых подмножеств A, B и C универсума U выполняются следующие основные булевы тождества:
- 12. Булевы тождества (продолжение) Теорема 4 (продолжение). 10 A\B = A ∩¬B
- 13. Булевы выражения
- 14. Булевы выражения 1. (A∪B∪C)\(C∩B) = (C÷B)U(A\(A∩B∩C))
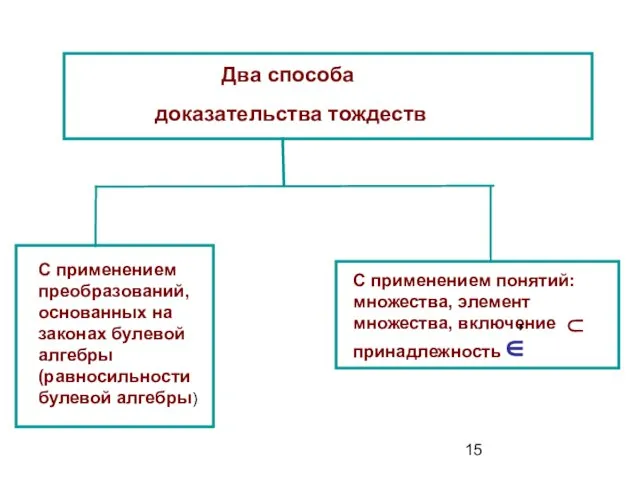
- 15. Два способа доказательства тождеств С применением преобразований, основанных на законах булевой алгебры (равносильности булевой алгебры) С
- 16. ДОКАЗАТЬ ТОЖДЕСТВА
- 17. Доказатьтождество A∪(B∩C) = (A∪B)∩(A∪C) . Решение. Сначала покажем, что A∪(B∩C) ⊆ (A∪B)∩(A∪C). Действительно, если x∈A∪(B∩C), то
- 18. Доказать тождества (самостоятельно) I. С помощью диаграмм Эйлера II. С помощью Булевых тождеств
- 19. Следующее утверждение докажите или опровергните (опровергнуть можно на частном примере с помощью диаграммы Эйлера: 1. (A\B)∪C
- 21. Скачать презентацию















 Сравнение трехзначных чисел
Сравнение трехзначных чисел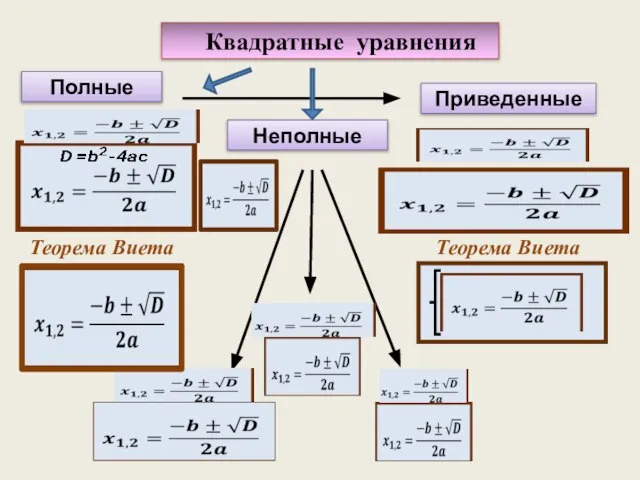 Квадратные уравнения
Квадратные уравнения Задание Квадрат
Задание Квадрат Преобразование графиков элементарных функций
Преобразование графиков элементарных функций Инвариант. Решение олимпиадных задач
Инвариант. Решение олимпиадных задач Гласные звуки и буквы. Слова с буквой Э
Гласные звуки и буквы. Слова с буквой Э Окружность. Вписанные углы
Окружность. Вписанные углы Презентация на тему Построение сечений многогранников
Презентация на тему Построение сечений многогранников  Метод координат
Метод координат Формулы приведения
Формулы приведения Способы решения систем линейных уравнений
Способы решения систем линейных уравнений Л 9 Бесконечно большие функции и замечательные пределы
Л 9 Бесконечно большие функции и замечательные пределы Аналитическая геометрия. Уравнения прямой
Аналитическая геометрия. Уравнения прямой Свойства предметов (часть 2)
Свойства предметов (часть 2) О числах
О числах Презентация на тему Решение планиметрических задач на нахождение геометрических величин
Презентация на тему Решение планиметрических задач на нахождение геометрических величин  Сложение и вычитание с переходом через десяток в пределах 10. Интерактивная игра-тренажер по математике Смешарики
Сложение и вычитание с переходом через десяток в пределах 10. Интерактивная игра-тренажер по математике Смешарики Таблица сложения
Таблица сложения Умножение и деление десятичных дробей
Умножение и деление десятичных дробей Решение квадратных неравенств
Решение квадратных неравенств Сложение двузначных и однозначных чисел с переходом в другой разряд
Сложение двузначных и однозначных чисел с переходом в другой разряд Многоугольник тетраэдр
Многоугольник тетраэдр Сложение и вычитание обыкновенных дробей с разными знаменателями
Сложение и вычитание обыкновенных дробей с разными знаменателями Схема Горнера
Схема Горнера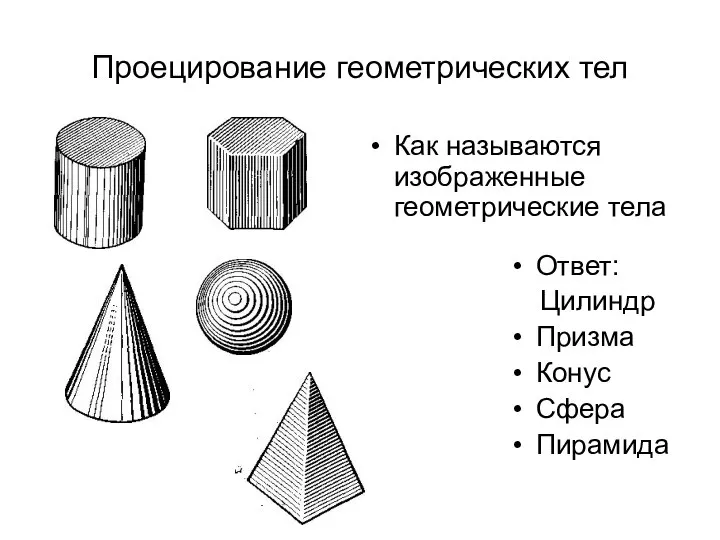 Построение геометрических тел
Построение геометрических тел Сумма углов треугольника
Сумма углов треугольника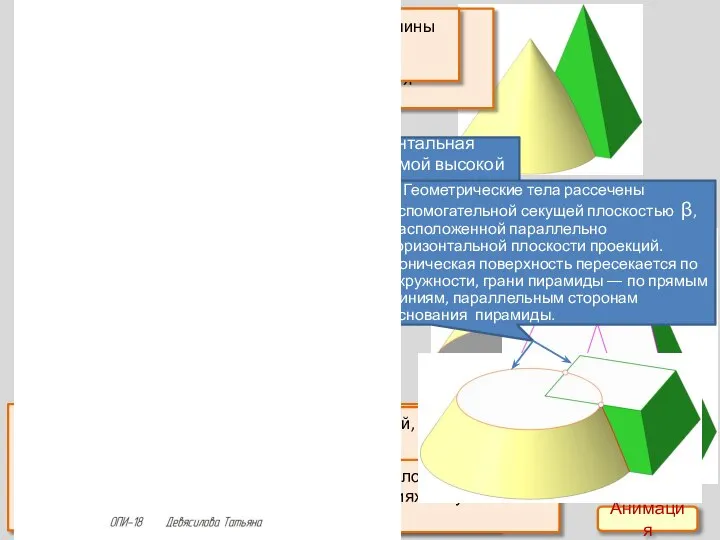 Пересечение поверхностей
Пересечение поверхностей Логарифмические уравнения
Логарифмические уравнения