Содержание
- 2. Предмет стереометрии СТЕРЕО (греч.) – объемный, пространственный; МЕТРЕО (греч.) – измерять. СТЕРЕОМЕТРИЯ – раздел геометрии, изучающий
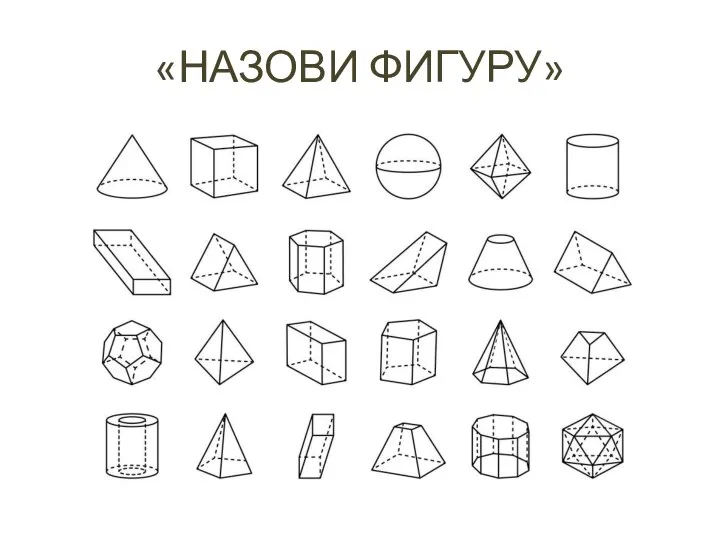
- 3. «НАЗОВИ ФИГУРУ»
- 5. МНОГОГРАННИКИ
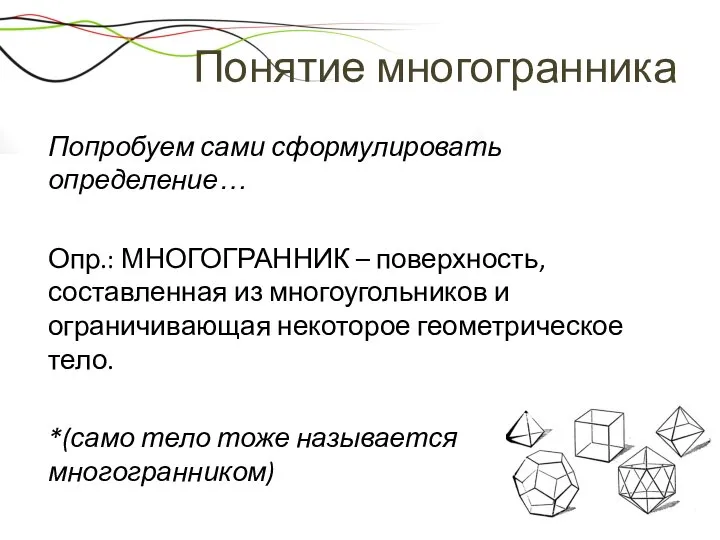
- 6. Понятие многогранника Попробуем сами сформулировать определение… Опр.: МНОГОГРАННИК – поверхность, составленная из многоугольников и ограничивающая некоторое
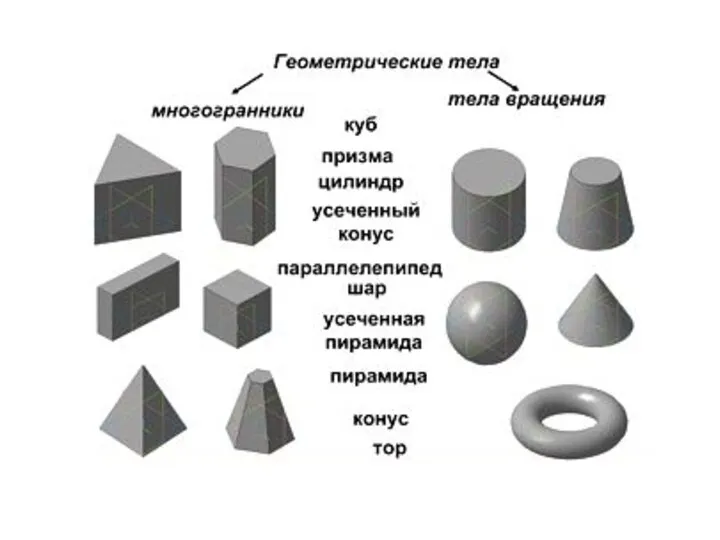
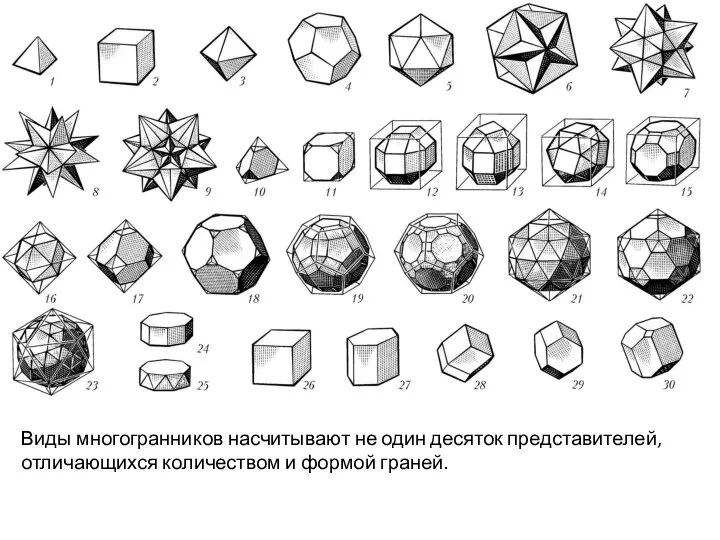
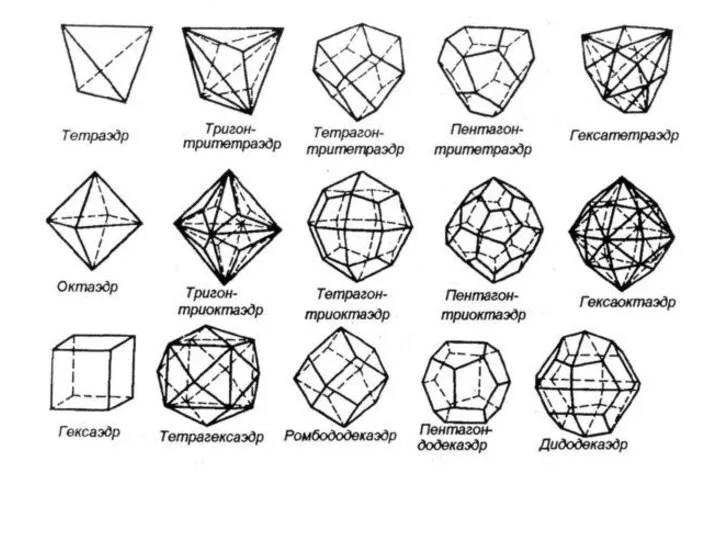
- 7. Виды многогранников насчитывают не один десяток представителей, отличающихся количеством и формой граней.
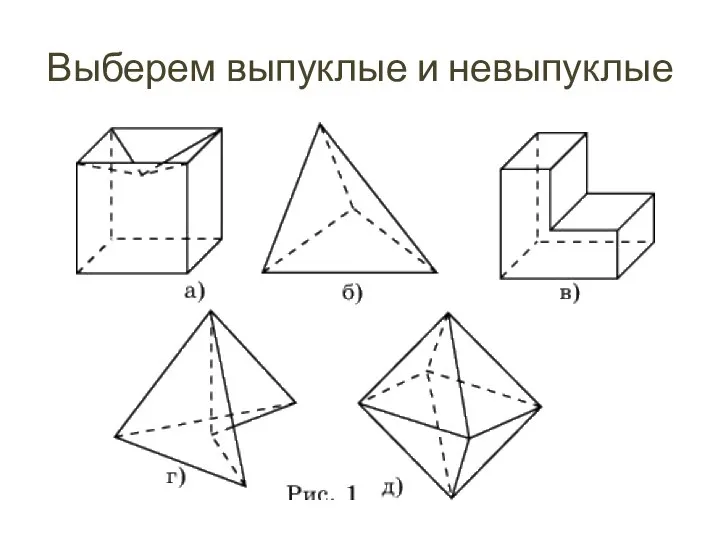
- 10. Многогранники делятся на: Выпуклые Многогранник называется выпуклым, если он расположен по одну сторону от плоскости каждой
- 11. Выберем выпуклые и невыпуклые
- 12. Общие свойства многогранников: Все они имеют 3 неотъемлемых компонента: грани – многоугольники, из которых составлен многогранник;
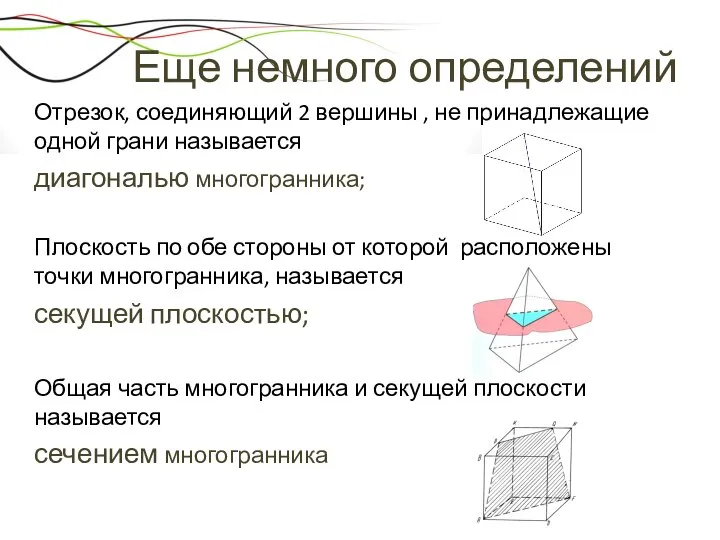
- 13. Еще немного определений Отрезок, соединяющий 2 вершины , не принадлежащие одной грани называется диагональю многогранника; Плоскость
- 14. Теорема Эйлера Леонард Эйлер (1707 - 1783) Th: В любом выпуклом многограннике сумма числа граней и
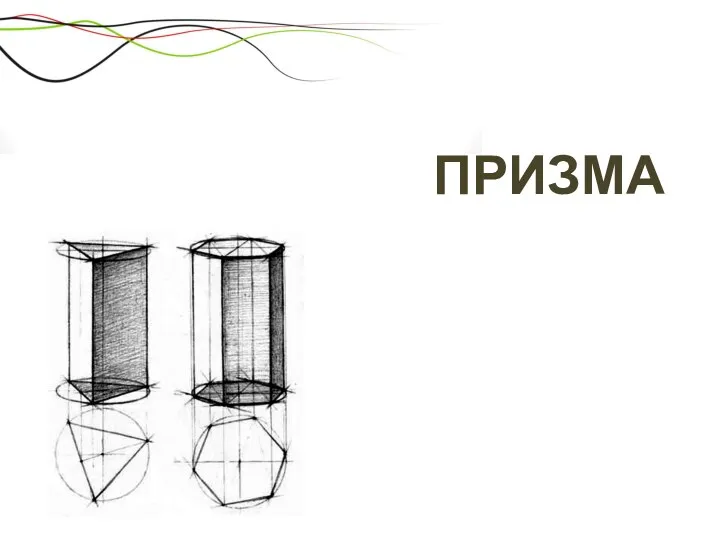
- 15. ПРИЗМА
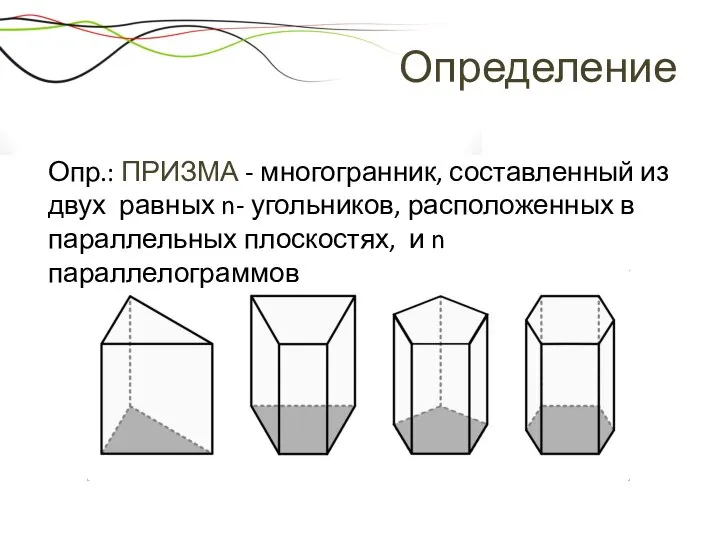
- 16. Определение Опр.: ПРИЗМА - многогранник, составленный из двух равных n- угольников, расположенных в параллельных плоскостях, и
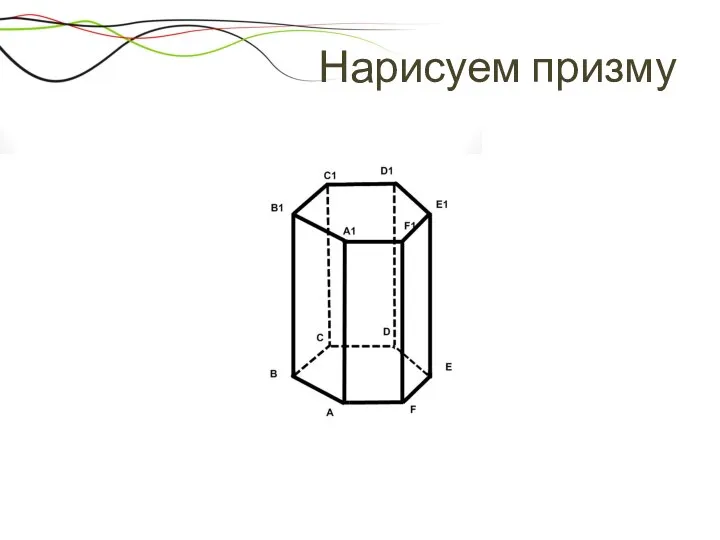
- 17. Нарисуем призму
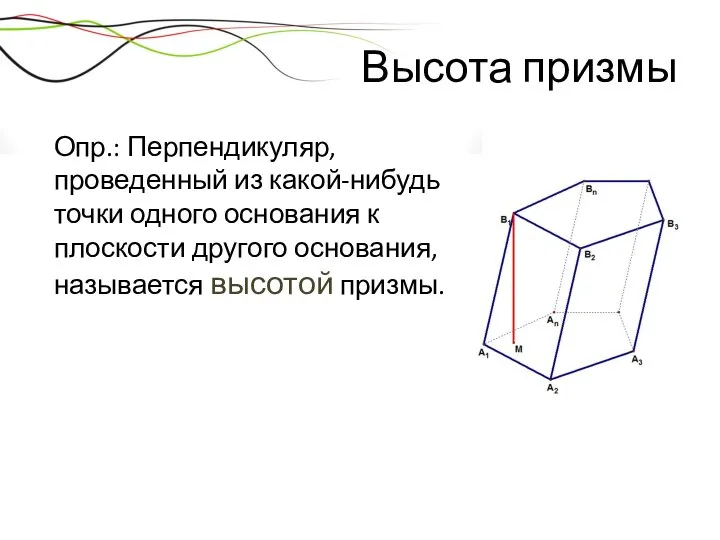
- 18. Высота призмы Опр.: Перпендикуляр, проведенный из какой-нибудь точки одного основания к плоскости другого основания, называется высотой
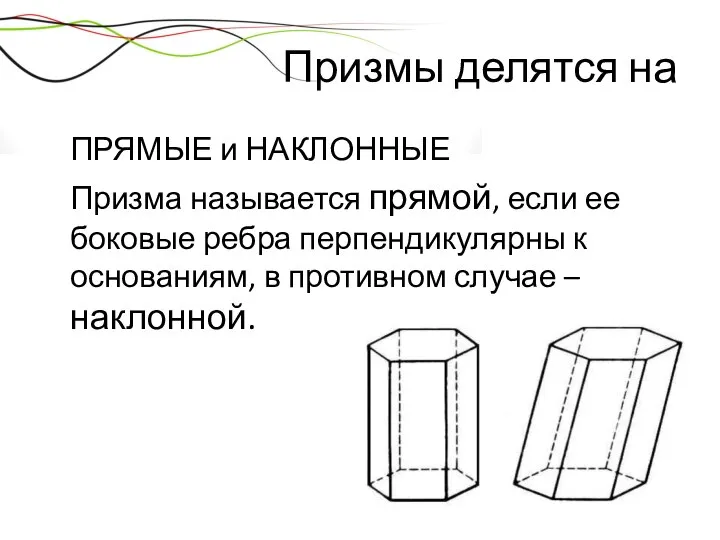
- 19. Призмы делятся на ПРЯМЫЕ и НАКЛОННЫЕ Призма называется прямой, если ее боковые ребра перпендикулярны к основаниям,
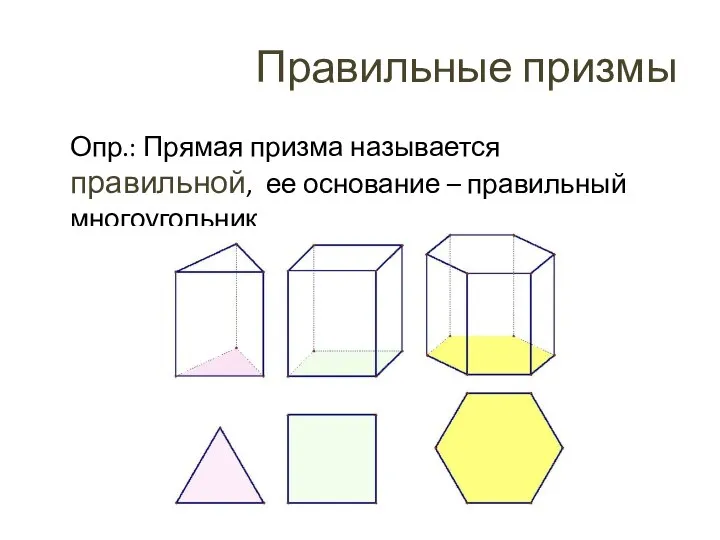
- 20. Правильные призмы Опр.: Прямая призма называется правильной, ее основание – правильный многоугольник
- 22. Скачать презентацию





 Презентация на тему Округление десятичных дробей
Презентация на тему Округление десятичных дробей  Конус
Конус Вычисление коэффициента корреляции и построение линии регрессии. Статистический анализ
Вычисление коэффициента корреляции и построение линии регрессии. Статистический анализ Геометрический конструктор: Развивающая игра Танграм
Геометрический конструктор: Развивающая игра Танграм Уравнение с двумя переменными и его график
Уравнение с двумя переменными и его график Сумма углов геометрических фигур
Сумма углов геометрических фигур Графический диктант: Формулы
Графический диктант: Формулы Презентация на тему Перпендикулярность
Презентация на тему Перпендикулярность  Психолого – педагогические основы организации математического развития младших школьников
Психолого – педагогические основы организации математического развития младших школьников Уравнение окружности
Уравнение окружности Тригонометрия задачки
Тригонометрия задачки Нумерация чисел
Нумерация чисел ЕГЭ 2012
ЕГЭ 2012 Проценты
Проценты Сложение чисел
Сложение чисел Координатная плоскость. Построение точки по ее координатам. 6 класс
Координатная плоскость. Построение точки по ее координатам. 6 класс Математика на страницах книг
Математика на страницах книг Сумма бесконечной геометрической прогрессии
Сумма бесконечной геометрической прогрессии Эрдниев Пюрвя Мучкаевич
Эрдниев Пюрвя Мучкаевич Стандартный вид числа в физике, астрономии и технике
Стандартный вид числа в физике, астрономии и технике Решение систем уравнений с двумя переменными методом подстановки
Решение систем уравнений с двумя переменными методом подстановки Презентация на тему Таблицы умножения и деления с числом 6
Презентация на тему Таблицы умножения и деления с числом 6  Численное решение нелинейных уравнений (метод итераций, метод хорд, комбинированный метод)
Численное решение нелинейных уравнений (метод итераций, метод хорд, комбинированный метод) Задания
Задания Геометрические фигуры (интерактивная игра)
Геометрические фигуры (интерактивная игра) Мой кабинет – моя лаборатория Презентацию подготовила заведующая школьным кабинетом математики №14 Ларионова Татьяна Ивановна.
Мой кабинет – моя лаборатория Презентацию подготовила заведующая школьным кабинетом математики №14 Ларионова Татьяна Ивановна. Способы решения линейных уравнений. 5-й класс
Способы решения линейных уравнений. 5-й класс Задачи на нахождение расстояния между вершинами многогранника, все двугранные углы которого, прямые
Задачи на нахождение расстояния между вершинами многогранника, все двугранные углы которого, прямые