Правильная пирамида

Прототип задания B9 (№ 284349)
В правильной четырехугольной пирамиде SABCD точка O — центр основания, S вершина, SC = 5, AC = 6. Найдите длину отрезка SO.
O
5
H
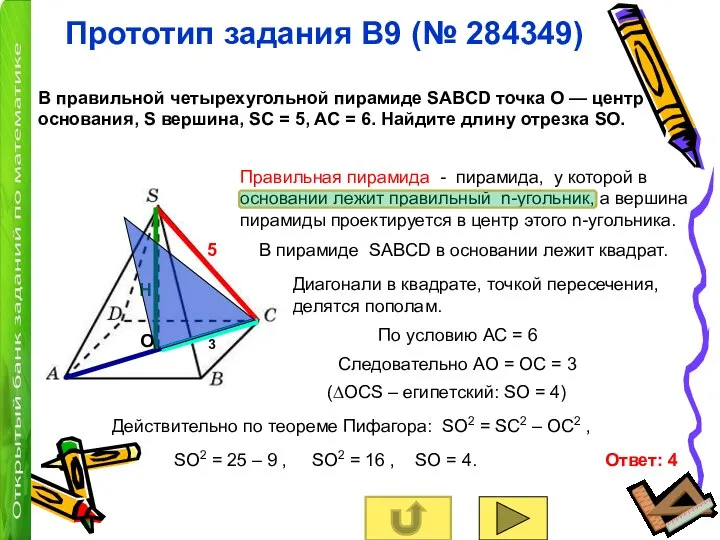
Правильная пирамида - пирамида, у которой в основании лежит правильный n-угольник, а вершина пирамиды проектируется в центр этого n-угольника.
В пирамиде SABCD в основании лежит квадрат.
По условию АС = 6
Диагонали в квадрате, точкой пересечения,
делятся пополам.
Следовательно АО = ОС = 3
3
(∆ОСS – египетский: SО = 4)
Действительно по теореме Пифагора: SО2 = SС2 – ОС2 ,
SО2 = 25 – 9 , SО2 = 16 , SО = 4.
Ответ: 4

Задание B9 (№ 284471)
В правильной четырехугольной пирамиде SABCD точка O — центр основания, S вершина, SC = 15, BD = 24. Найдите длину отрезка SO.
O
15
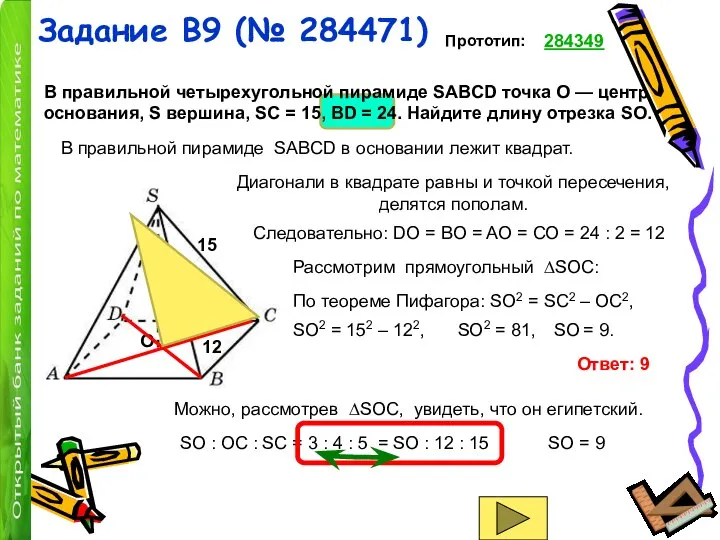
Следовательно: DO = BO = AO = CO = 24 : 2 = 12
В правильной пирамиде SABCD в основании лежит квадрат.
Диагонали в квадрате равны и точкой пересечения,
делятся пополам.
12
Рассмотрим прямоугольный ∆SOC:
По теореме Пифагора: SO2 = SС2 – ОС2,
SO2 = 152 – 122,
SO2 = 81,
SO = 9.
Можно, рассмотрев ∆SOC, увидеть, что он египетский.
Ответ: 9
SO : ОС : SС = 3 : 4 : 5 = SO : 12 : 15
SO = 9

Задание B9 (№ 284563)
В правильной четырехугольной пирамиде SABCD точка O — центр основания, S вершина, SA = 13, AC = 24. Найдите длину отрезка SO.
O
13
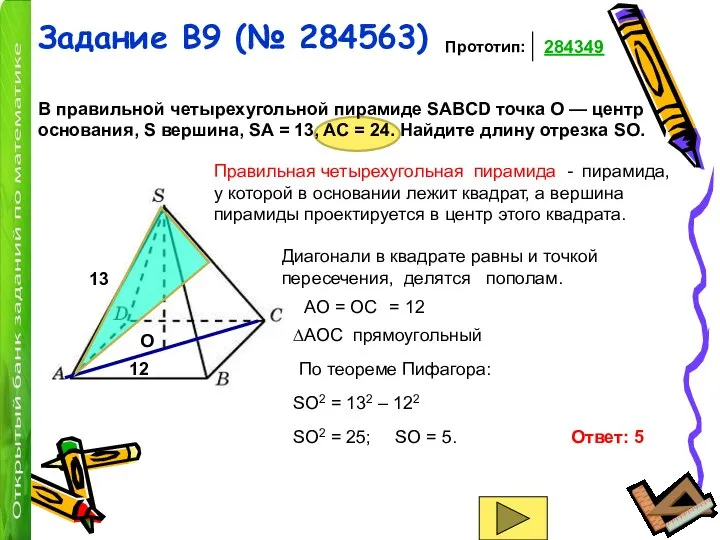
Правильная четырехугольная пирамида - пирамида, у которой в основании лежит квадрат, а вершина пирамиды проектируется в центр этого квадрата.
Диагонали в квадрате равны и точкой пересечения, делятся пополам.
АО = ОС
= 12
12
∆AOC прямоугольный
По теореме Пифагора:
SO2 = 132 – 122
SO2 = 25;
SO = 5.
Ответ: 5

Прототип задания B9 (№ 284350)
В правильной четырехугольной пирамиде SABCD точка O — центр основания, S вершина, SO = 4, SC = 5. Найдите длину отрезка AC.
O
4
5
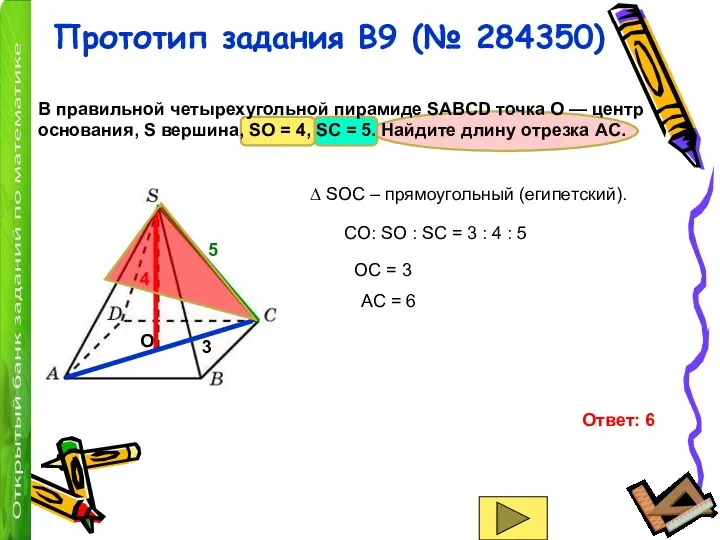
∆ SOC – прямоугольный (египетский).
CO: SO : SC = 3 : 4 : 5
3
OC = 3
АС = 6
Ответ: 6