Многоранники

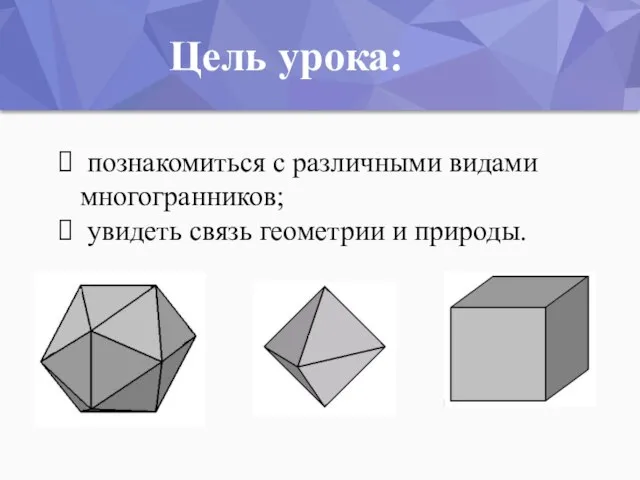
познакомиться с различными видами многогранников;
увидеть связь геометрии и природы.
Цель урока:

Организационный момент
Усвоение нового материала
Закрепление новых знаний
Решение задач Подведение итога урока
Домашнее задание
План урока

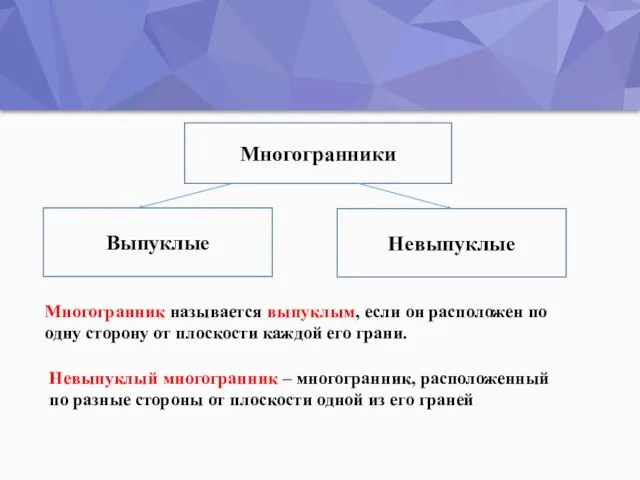
Многогранником называется тело, граница которого является объединением конечного числа многоугольников.

Многогранники
Выпуклые
Невыпуклые
Многогранник называется выпуклым, если он расположен по одну сторону от плоскости каждой его грани.
Невыпуклый многогранник – многогранник, расположенный по разные стороны от плоскости одной из его граней.

Типы правильных многогранников
Правильный многогранник — это выпуклый многогранник с максимально возможной симметрией

Тетра́эдр
(греч. τετραεδρον - четырёхгранник) —многогранник с четырьмя треугольными гранями, в каждой из вершин которого сходятся по 3 грани. У тетраэдра
4 грани,
4 вершины,
6 рёбер.

Окта́эдр
(греч.(греч. οκτάεδρον, от греч.(греч. οκτάεδρον, от греч. οκτώ, «восемь» и греч.έδρα - «основание»). Октаэдр-восьмигранник, тело, ограниченное восемью правильными треугольниками.
Октаэдр имеет
8 треугольных граней,
12 рёбер,
6 вершин,
в каждой его вершине сходятся 4 ребра.

Куб или правильный гексаэдр - правильный многогранник, каждая грань которого представляет собой квадрат. Куб или правильный гексаэдр - правильная четырех-угольная призма с равными ребрами, ограниченная шестью квадратами Частный случай параллелепипеда и призмы.

Икоса́эдр
(от греч. εικοσάς — двадцать; -εδρον — грань, лицо, основание) — правильный выпуклый многогранник, двадцати-гранник. Каждая из 20 граней представляет собой равносторонний треугольник. У икосаэдра
30 ребер,
12 вершин,
59 звездчатых форм.

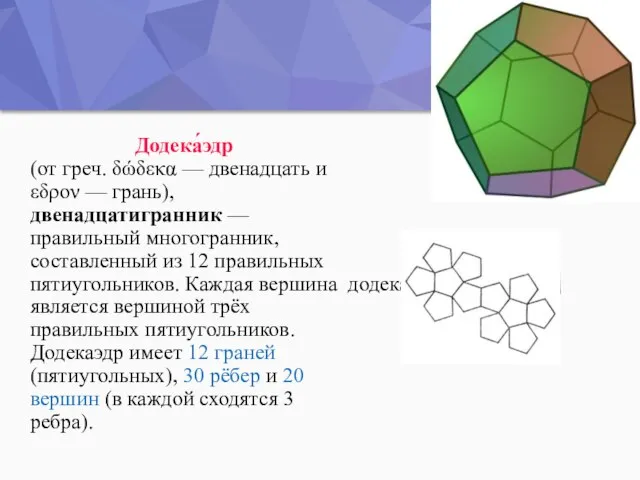
Додека́эдр
(от греч. δώδεκα — двенадцать и εδρον — грань), двенадцатигранник —правильный многогранник, составленный из 12 правильных пятиугольников. Каждая вершина додекаэдра является вершиной трёх правильных пятиугольников.
Додекаэдр имеет 12 граней (пятиугольных), 30 рёбер и 20 вершин (в каждой сходятся 3 ребра).

ВЫВОД: существует пять выпуклых правильных многогранников - тетраэдр, октаэдр и икосаэдр с треугольными гранями, куб (гексаэдр) с квадратными гранями и додекаэдр с пятиугольными гранями.
Названия этих многогранников пришли из Древней Греции, и в них указывается число граней:
«эдра» - грань
«тетра» - 4
«гекса» - 6
«окта» - 8
«икоса» - 20
«додека» - 12

Тетраэдр
Икосаэдр
Гексаэдр
Додекаэдр
Октаэдр

Многогранники в архитектуре
Великая пирамида в Гизе
Эта грандиозная Египетская пирамида является древнейшим из Семи чудес древности. Великая пирамида была построена как гробница Хуфу, известного грекам как Хеопс. Он был одним из фараонов, или царей древнего Египта, а его гробница была завершена в 2580 году до н.э. Позднее в Гизе было построено еще две пирамиды, для сына и внука Хуфу, а также меньшие по размерам пирамиды для их цариц.

Три башни
Фаросский маяк состоял из трех мраморных башен, стоявших на основании из массивных каменных блоков. Первая башня была прямоугольной, в ней находились комнаты, в которых жили рабочие и солдаты. Над этой башней располагалась меньшая, восьмиугольная башня со спиральным пандусом, ведущим в верхнюю башню.

Многогранники в искусстве
Знаменитый художник, увлекавшийся геометрией, Альбрехт Дюрер (1471- 1528) , в известной гравюре ''Меланхолия '‘ на переднем плане изобразил додекаэдр.
Сальвадор Дали на картине «Тайная вечеря» изобразил И. Христа со своими учениками на фоне огромного прозрачного додекаэдра.

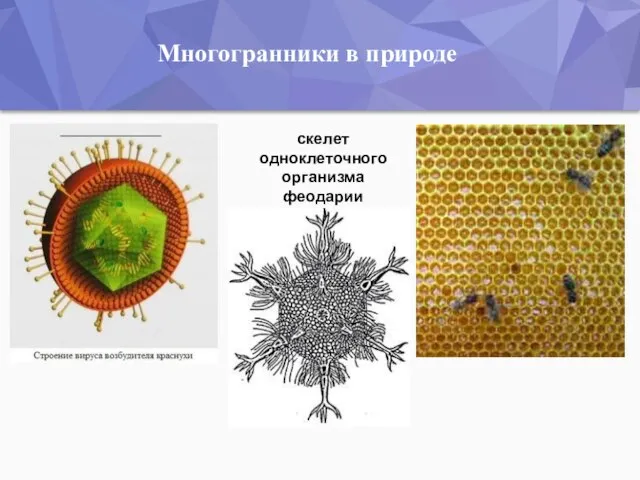
Многогранники в природе
скелет одноклеточного организма феодарии