фигур. Стереометрия — греческое слово. Оно произошло от слов "стерео" - тело и "метрио" - измерять, т.е. буквально стереометрия означает "теломерие". Стереометрия, как и планиметрия, возникла и развивалась в связи с потребностями практической деятельности человека. О зарождении геометрии в древнем Египте около 2000 лет до н.э. древнегреческий ученый Геродот (V в. до н.э.) писал следующее: "Сеозоострис, египетский фараон, разделил землю, дав каждому египтянину участок по жребию и взимал соответствующим образом налог с каждого участка. Случалось, что Нил заливал тот или иной участок, тогда пострадавший обращался к царю, а царь посылал землемеров, чтобы установить, на сколько уменьшился участок, и соответствующим образом уменьшить налог. Так возникла геометрия в Египте, а оттуда перешла в Грецию".
Одной из самых первых и самых известных школ была пифагорейская (VI-V вв.до н. э.), названная так в честь своего основателя Пифагора. Для своих философских теорий пифагорейцы использовали правильные многогранники, формы которых придавали элементам первооснов бытия, а именно: огонь – тетраэдр, земля - гексаэдр (куб); воздух – октаэдр; вода – икосаэдр; вся Вселенная, по мнению древних, имела форму додекаэдра.
Стереометрия







 Дискретная математика. Основные понятия и определения графа и его элементов
Дискретная математика. Основные понятия и определения графа и его элементов Старинный способ решения задач на смеси и сплавы
Старинный способ решения задач на смеси и сплавы Поняття та призначення функцій
Поняття та призначення функцій Математика
Математика Векторное исчисление
Векторное исчисление История возникновения геометрии как науки
История возникновения геометрии как науки Смежные и вертикальные углы. Решение задач
Смежные и вертикальные углы. Решение задач Формулы сокращенного умножения
Формулы сокращенного умножения Описание линейной дискретной системы в частотной области (ЛДС). Частотные характеристики ЛДС
Описание линейной дискретной системы в частотной области (ЛДС). Частотные характеристики ЛДС Единицы времени. Час. минута
Единицы времени. Час. минута Презентация на тему Дифференцирование частного и степени
Презентация на тему Дифференцирование частного и степени  Простейшие векторные операции и их реализация на языке MATLAB
Простейшие векторные операции и их реализация на языке MATLAB Теория вероятности в жизни пчел
Теория вероятности в жизни пчел Теорема Пифагора
Теорема Пифагора Задачи на проценты. ОГЭ
Задачи на проценты. ОГЭ Презентация на тему Осевая симметрия
Презентация на тему Осевая симметрия  Прибавить и вычесть 3. Решение текстовых задач. Урок №57
Прибавить и вычесть 3. Решение текстовых задач. Урок №57 Презентация на тему Иррациональные уравнения
Презентация на тему Иррациональные уравнения 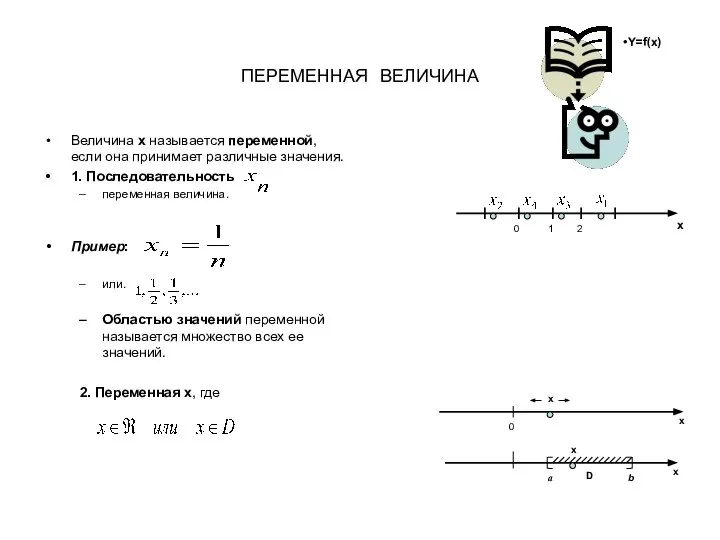 Понятие функции, предел
Понятие функции, предел Иррациональные уравнения
Иррациональные уравнения Путешествие в страну математики. Дидактическая игра Веселые цифры
Путешествие в страну математики. Дидактическая игра Веселые цифры Презентация на тему График квадратичной функции. Неравенства с одной переменной
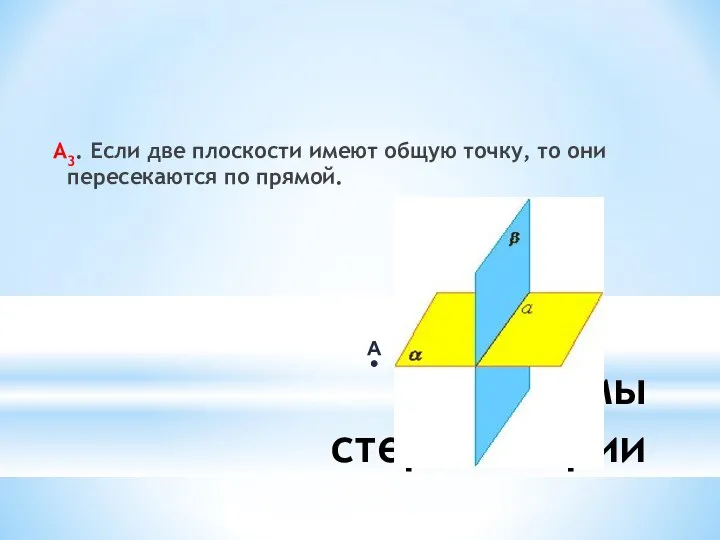
Презентация на тему График квадратичной функции. Неравенства с одной переменной  Тема урока: «Аксиомы стереометрии и их следствия. Решение задач»
Тема урока: «Аксиомы стереометрии и их следствия. Решение задач» Прямоугольник, ромб, квадрат
Прямоугольник, ромб, квадрат Умножение числа на произведение
Умножение числа на произведение Графическое решение уравнений
Графическое решение уравнений Морской бой
Морской бой Круглые числа
Круглые числа