Содержание
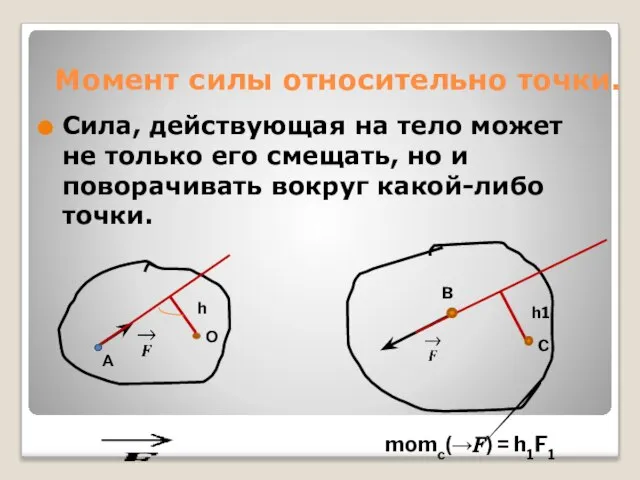
- 2. Момент силы относительно точки. Сила, действующая на тело может не только его смещать, но и поворачивать
- 3. Моментом силы F относительно центра О называется величина, равная произведению силы на кратчайшее расстояние от точки
- 4. Пара сил Система двух равных по модулю, параллельных и противоположно направленных сил, приложенных к телу, называется
- 5. Момент пары сил Плечом пары сил называется кратчайшее расстояние между линиями действия сил, составляющих пару. Моментом
- 6. Свойства пары сил
- 7. Контрольные вопросы 1. Что такое сила? 2. Какие силы называются уравновешивающими? 3. Что называется равнодействующей силой?
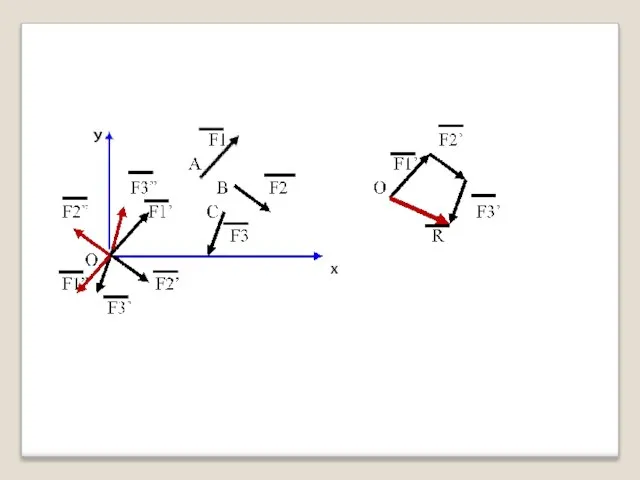
- 8. Плоская произвольная система сил На твердое тело действует произвольная система сил F1, F2, F3 (рис.1.17,а). Приложим
- 9. Х У
- 10. Теперь на тело действует система сходящихся сил F1’, F2’, F3’. И система пар сил с моментами
- 11. В результате приведения всех сил к точке, определяем, что Произвольную плоскую систему сил можно заменить одной
- 12. Точка О – называется центром приведения. Вектор R – главный вектор не зависит от центра приведения.
- 14. Скачать презентацию









 Старинные меры веса, длины и старинные денежные единицы (задачи для учащихся 5-6 классов)
Старинные меры веса, длины и старинные денежные единицы (задачи для учащихся 5-6 классов) Свойства равнобедренного треугольника
Свойства равнобедренного треугольника Диаграммы и графики. 6 класс
Диаграммы и графики. 6 класс Продолжение решения задач на движение
Продолжение решения задач на движение Решение неравенств второй степени. Алгоритм решения
Решение неравенств второй степени. Алгоритм решения Ортогональне проектування
Ортогональне проектування Соответствия между множествами. Отображения. Функции
Соответствия между множествами. Отображения. Функции Презентация на тему Теоремы синусов и косинусов
Презентация на тему Теоремы синусов и косинусов  Геометрический и физический смысл производной
Геометрический и физический смысл производной Старинные рычажные безмены
Старинные рычажные безмены Квадратичная функция и её график
Квадратичная функция и её график Применение производной функции для отыскания точек экстремума
Применение производной функции для отыскания точек экстремума Урок математики в 3 классе
Урок математики в 3 классе Угол. Виды углов. Опрос
Угол. Виды углов. Опрос Что? Где? Когда?
Что? Где? Когда? Асимптотические методы. Граничные условия на горизонтальной скважине. (Лекция 3)
Асимптотические методы. Граничные условия на горизонтальной скважине. (Лекция 3) Презентация на тему Угол между прямыми. Угол между прямой и плоскостью
Презентация на тему Угол между прямыми. Угол между прямой и плоскостью  Неопределённый интеграл
Неопределённый интеграл Критерий Манна-Уитни
Критерий Манна-Уитни Натуральный ряд чисел
Натуральный ряд чисел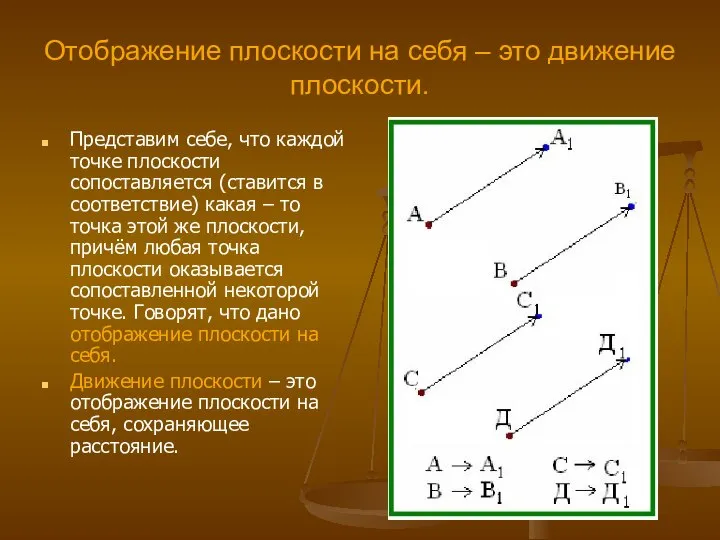 Геометрические преобразования плоскости
Геометрические преобразования плоскости Перестановки, размещения, сочетания без повторений
Перестановки, размещения, сочетания без повторений Презентация на тему Нахождение процента от числа
Презентация на тему Нахождение процента от числа  Деловая игра Маркетинг инноваций
Деловая игра Маркетинг инноваций Трёхчлен
Трёхчлен Дифференциальные исчисления. Конспект
Дифференциальные исчисления. Конспект Сложение и вычитание вида +1 -1
Сложение и вычитание вида +1 -1 Тест для учащихся 1 класса
Тест для учащихся 1 класса