Коэффициент корреляции

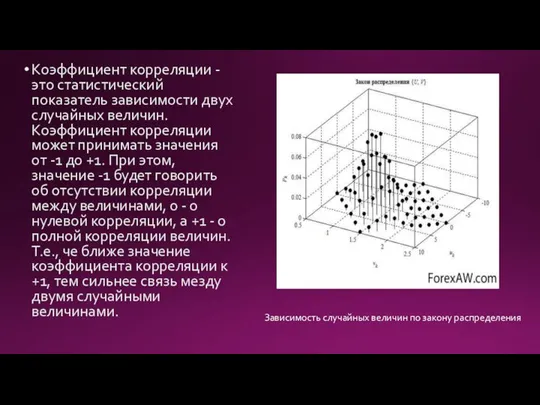
Коэффициент корреляции - это статистический показатель зависимости двух случайных величин. Коэффициент корреляции может принимать значения от -1 до +1. При этом, значение -1 будет говорить об отсутствии корреляции между величинами, 0 - о нулевой корреляции, а +1 - о полной корреляции величин. Т.е., че ближе значение коэффициента корреляции к +1, тем сильнее связь мезду двумя случайными величинами.
Зависимость случайных величин по закону распределения

Корреляцинное отношение, математическая мера корреляции двух случайных величин. В случае, если изменение одной случайной величины не ведёт к закономерному изменению другой случайной величины, но приводит к изменению другой статистической характеристики данной случайной величины, то подобная связь не считается корреляционной, хотя и является статистической.
Коэффициент корреляции - это мера линейной зависимости двух случайных величин в теории вероятностей и статистике. Некоторые виды коэффициентов корреляции могут быть положительными или отрицательными. В первом случае предполагается, что мы можем определить только наличие или отсутствие связи, а во втором - также и её направление.

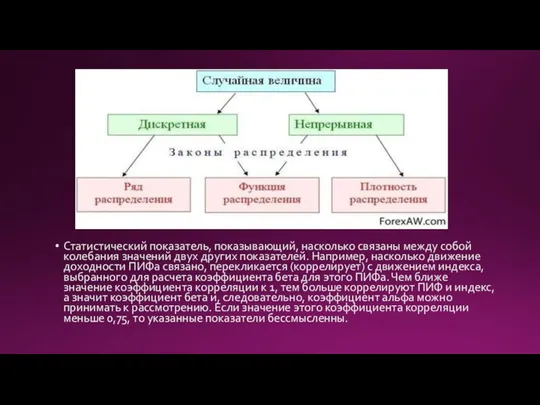
Статистический показатель, показывающий, насколько связаны между собой колебания значений двух других показателей. Например, насколько движение доходности ПИФа связано, перекликается (коррелирует) с движением индекса, выбранного для расчета коэффициента бета для этого ПИФа. Чем ближе значение коэффициента корреляции к 1, тем больше коррелируют ПИФ и индекс, а значит коэффициент бета и, следовательно, коэффициент альфа можно принимать к рассмотрению. Если значение этого коэффициента корреляции меньше 0,75, то указанные показатели бессмысленны.

Коэффициент корреляции - это математическая мера корреляции двух величин. В том случае, когда изменение одной из величин не приводит к закономерному изменению другой величины, то можно говорить об отсутствии корреляции между этими величинами. Коэффициенты корреляции могут быть положительными и отрицательными. Если при увеличении значения одной величины происходит уменьшение значений другой величины, то их коэффициент корреляции отрицательный. В случае, когда увеличение значений первого объекта наблюдения приводит к увеличениям значения второго объекта, то можно говорить о положительном коэффициенте.

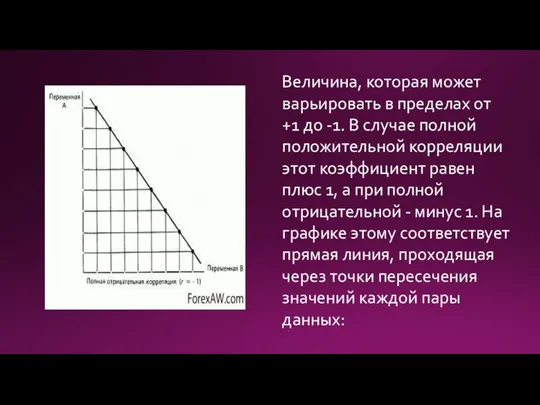
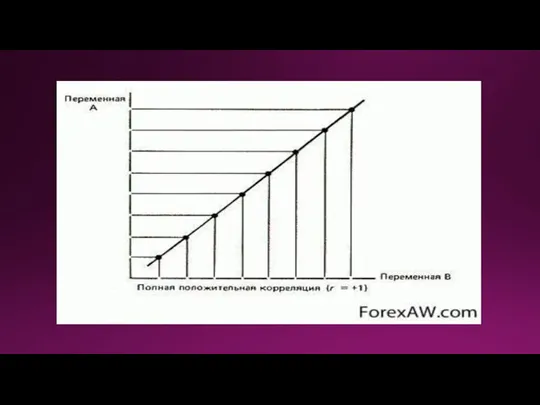
Величина, которая может варьировать в пределах от +1 до -1. В случае полной положительной корреляции этот коэффициент равен плюс 1, а при полной отрицательной - минус 1. На графике этому соответствует прямая линия, проходящая через точки пересечения значений каждой пары данных:

В то время как задача корреляционного анализа - установить, являются ли данные случайные величины взаимосвязанными, цель регрессионного анализа - описать эту связь аналитической зависимостью, т.е. с помощью уравнения. Мы рассмотрим самый несложный случай, когда связь между точками на графике может быть представлена прямой линией. Зная уравнение прямой, мы можем находить значение функции по значению аргумента в тех точках, где значение Х известно, а Y - нет. Эти оценки бывают очень нужны, но они должны использоваться осторожно, особенно, если связь между величинами не слишком тесная. Отметим также, что из сопоставления формул для b и r видно, что коэффициент не дает значение наклона прямой, а лишь показывает сам факт наличия связи.
Термин "корреляция" означает "связь". В эконометрике этот термин обычно используется в сочетании "коэффициенты корреляции". Рассмотрим линейный и непараметрические парные коэффициенты корреляции. Обсудим способы измерения связи между двумя случайными переменными. Пусть исходными данными является набор случайных векторов:

Выборочным коэффициентом корреляции, более подробно, выборочным линейным парным коэффициентом корреляции К. Пирсона, как известно, называется число:
Число - выборочный линейный парный коэффициент корреляции
Значение выборочного коэффициента корреляции

Таким образом, близость коэффициента корреляции к 1 (по абсолютной величине) говорит о достаточно тесной линейной связи. Если случайные векторанезависимы и одинаково распределены, то выборочный коэффициент корреляции сходится к теоретическому при безграничном возрастании объема выборки (сходимость по вероятности):
Безграничное возрастание объема выборки выборочного коэффициента корреляции

Более того, выборочный коэффициент корреляции является асимптотически нормальным. Это означает, что
Асимптотически нормальный выборочный коэффициент корреляции
Переменные выборочного коэффициента корреляции

Коэффициенты корреляции типа rn используются во многих алгоритмах многомерного статистического анализа. В теоретических рассмотрениях часто считают, что случайные вектора имеют двумерное нормальное распределение. Распределения реальных данных, как правило, отличны от нормальных. Почему же распространено представление о двумерном нормальном распределении? Дело в том, что теория в этом случае проще. В частности, равенство 0 теоретического коэффициента корреляции эквивалентно независимости случайных величин. Поэтому проверка независимости сводится к проверке статистической гипотезы о равенстве 0 теоретического коэффициента корреляции. Эта гипотеза принимается, если

Свойства коэффициента корреляции Коэффициент корреляции р для генеральной совокупности, как правило, неизвестен, поэтому он оценивается по экспериментальным данным, представляющим собой выборку объема n пар значений (Xi, Yi), полученную при совместномизмерении двух признаков Х и Y. Коэффициент корреляции, определяемый по выборочным данным, называется выборочным коэффициентом корреляции (или просто коэффициентом корреляции). Его принято обозначать символом r.

Оценка корреляционной связи по коэффициенту корреляции При изучении корреляционной связи важным направлением анализа является оценка степени тесноты связи. Понятие степени тесноты связи между двумя признаками возникает вследствие того, что в реальной действительности на изменение результативного признака влияют несколько факторов. При этом влияние одного из факторов может выражаться более заметно и четко, чем влияние других факторов. С изменением условий в качестве главного, решающего фактора может выступать другой.