Содержание
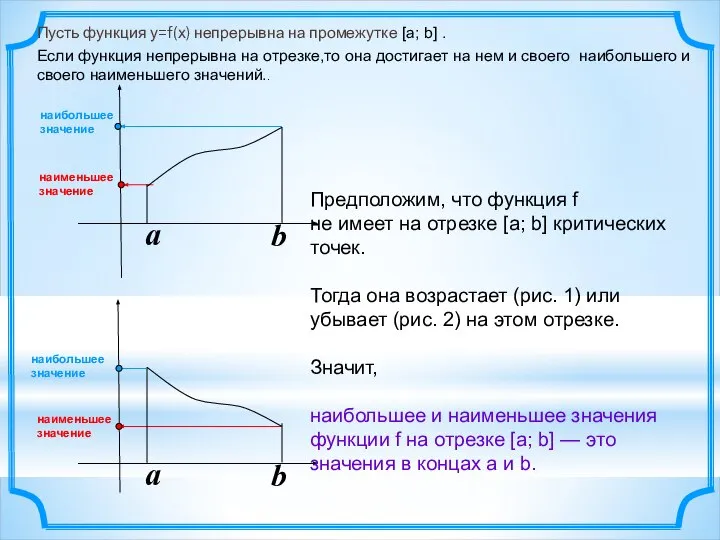
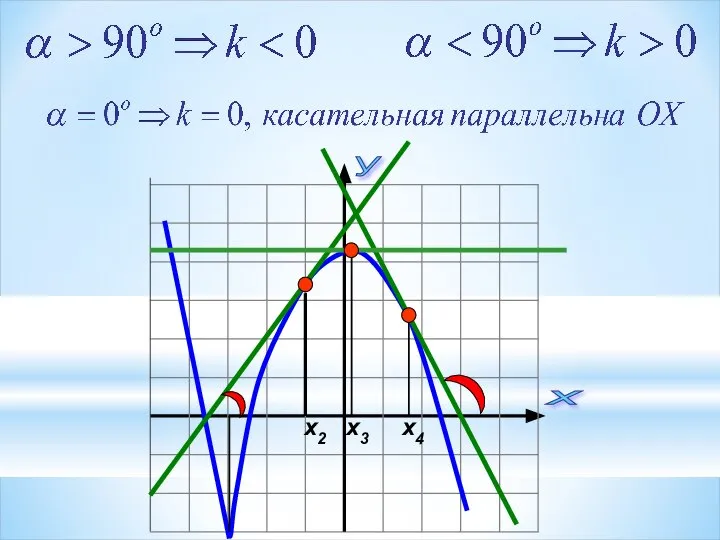
- 2. a b a b Предположим, что функция f не имеет на отрезке [а; b] критических точек.
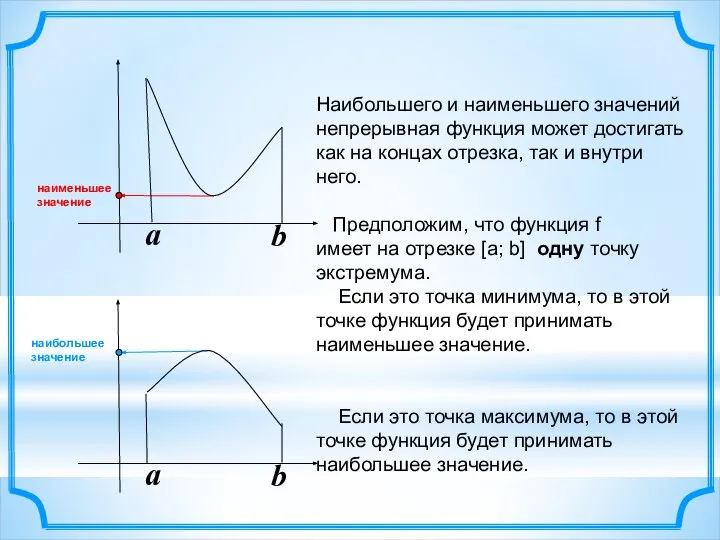
- 3. a b a b Наибольшего и наименьшего значений непрерывная функция может достигать как на концах отрезка,
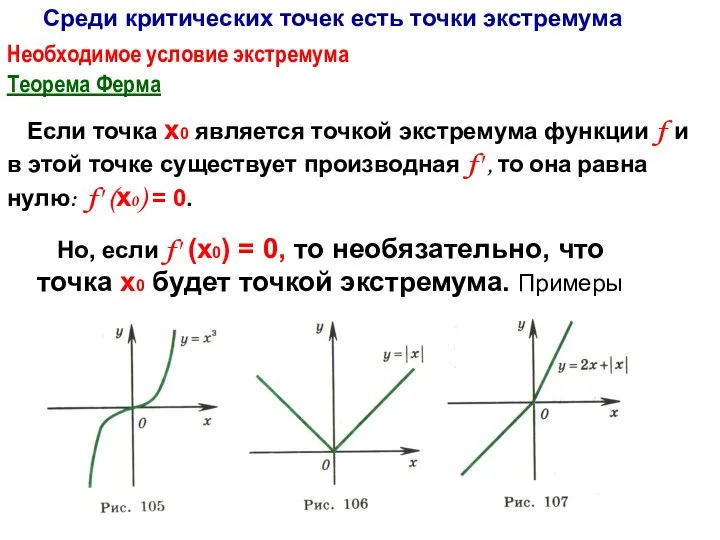
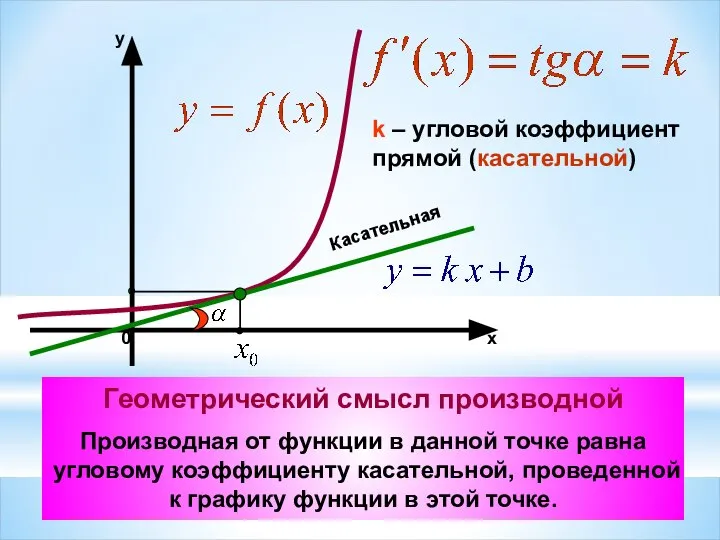
- 5. Теорема Ферма Если точка х0 является точкой экстремума функции f и в этой точке существует производная
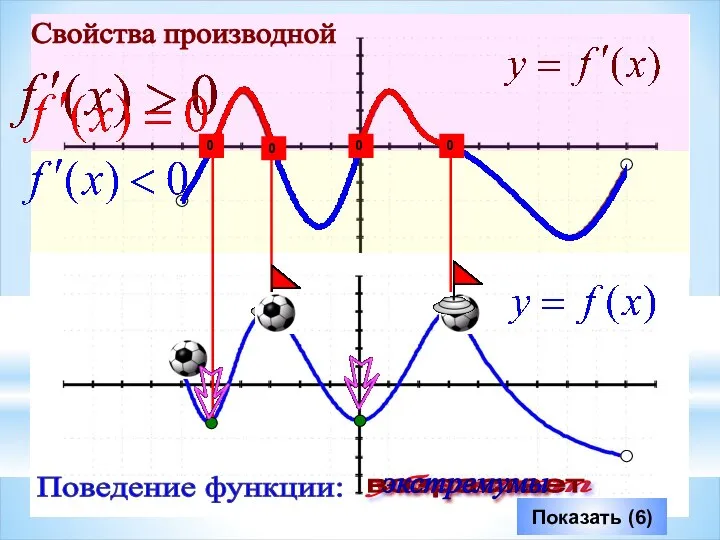
- 7. Показать (6) убывает возрастает экстремумы
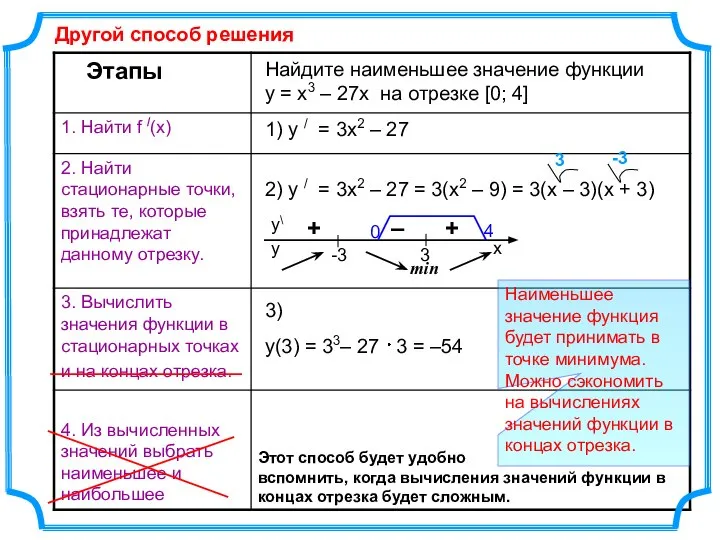
- 9. Найдите наименьшее значение функции y = x3 – 27x на отрезке [0; 4] 1) y /
- 10. Найдите наименьшее значение функции y = x3 – 27x на отрезке [0; 4] 1) y /
- 11. Найдите наибольшее значение функции 2. x = – 2 Найдем критические точки, которые принадлежат D(у). Вычислим
- 12. Найдите наибольшее значение функции Решим задание без вычисления производной Функция наименьшее значение будет иметь тогда ,
- 13. Найти наибольшее и наименьшее значение функции y= x2 - 3x + 5 + |1-x| на отрезке
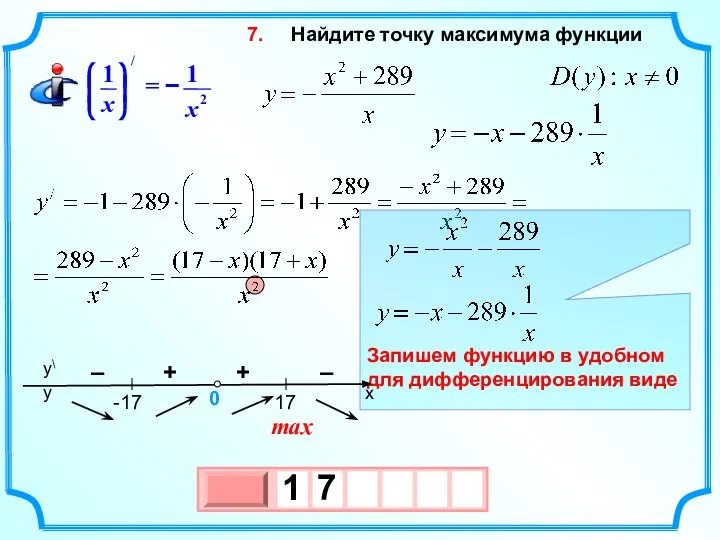
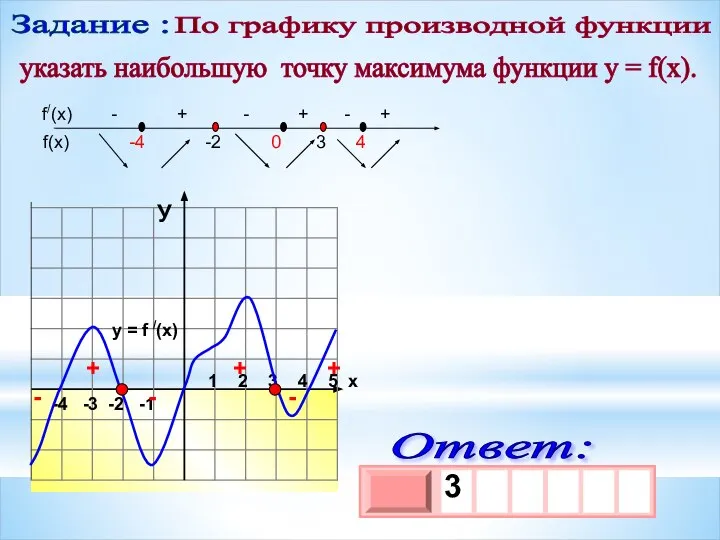
- 14. Найдите точку максимума функции 7. max + – – +
- 15. -4 -3 -2 -1 1 2 3 4 5 х y = f /(x) + +
- 18. Скачать презентацию





 Вредная задача
Вредная задача Ряды
Ряды Урок по теме Математика 6 класс Подготовлено Гаенко Т.А. Акимовская школа №3 Запорожской обл.
Урок по теме Математика 6 класс Подготовлено Гаенко Т.А. Акимовская школа №3 Запорожской обл. Конструирование из геометрических фигур
Конструирование из геометрических фигур Элементы комбинаторики. Лекция 111
Элементы комбинаторики. Лекция 111 Теорема синусов
Теорема синусов Системы уравнений. Задание №9. ОГЭ
Системы уравнений. Задание №9. ОГЭ Повторение курса алгебры (7 класс)
Повторение курса алгебры (7 класс) Линейные пространства
Линейные пространства Случаи вычитания 11-
Случаи вычитания 11- Презентация на тему Масштаб и его практическое применение
Презентация на тему Масштаб и его практическое применение  Неравенства системы и совокупности неравенств
Неравенства системы и совокупности неравенств Основные теоремы теории вероятностей. Лекция 3
Основные теоремы теории вероятностей. Лекция 3 Таблица умножения на 3
Таблица умножения на 3 Методика изучения времени. Время
Методика изучения времени. Время Свойства параллелограмма
Свойства параллелограмма ложение комплексных чисел. Вычитание комплексных чисел
ложение комплексных чисел. Вычитание комплексных чисел Задача 6.15 из сборника задач к начальному курсу эконометрики
Задача 6.15 из сборника задач к начальному курсу эконометрики Презентация на тему Леонтий Филиппович Магницкий
Презентация на тему Леонтий Филиппович Магницкий  Обратные тригонометрические функции
Обратные тригонометрические функции Центральные и вписанные углы
Центральные и вписанные углы Презентация на тему Округление десятичных дробей
Презентация на тему Округление десятичных дробей  Zaokrugljivanje decimalnih brojeva
Zaokrugljivanje decimalnih brojeva Экскурсия в мир чисел
Экскурсия в мир чисел Геометрические фигуры
Геометрические фигуры Квадратные уравнения
Квадратные уравнения Экологические понятия в математике
Экологические понятия в математике Перпендикуляр к прямой. Медианы, биссектрисы и высоты треугольника
Перпендикуляр к прямой. Медианы, биссектрисы и высоты треугольника