Содержание
- 2. Множеством называется совокупность некоторых элементов, объединенных каким-либо общим признаком.
- 3. Элементами множества могут быть числа, фигуры, предметы, понятия и т.п. Множества обозначаются прописными буквами, а элементы
- 4. А={1, 2, 3, 4, 5, 6, 7, 8, 9} В={а, б, в, г, д, е, ё,
- 5. Операции над множествами Два множества А и В равны (А=В), если они состоят из одних и
- 6. Операции над множествами Объединением (суммой) множеств А и В называется множество А ∪ В, элементы которого
- 7. Операции над множествами Пересечением (произведением) множеств А и В называется множество А ∩ В, элементы которого
- 8. Операции над множествами Разностью множеств А и В называется множество А\В, элементы которого принадлежат множеству А,
- 9. Определить множества A U B, A ∩ B, A\B, B\A A={1,2,3,4,5, a, b}, B={3,5,7,b,k} Решение задач
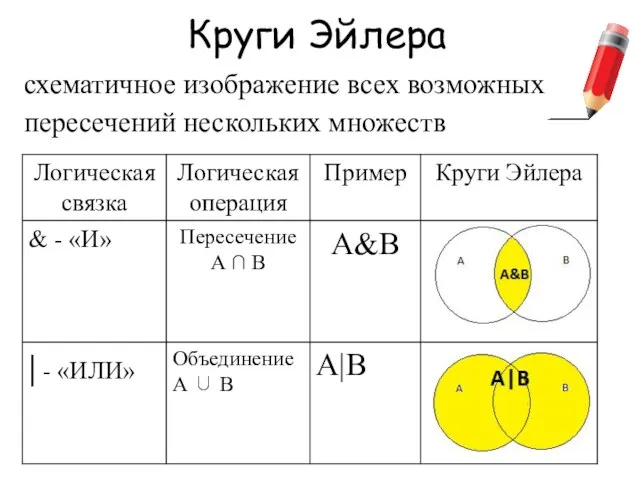
- 10. Круги Эйлера схематичное изображение всех возможных пересечений нескольких множеств
- 11. Решение задач Лебедь | Рак | Щука
- 12. Лебедь & Рак
- 13. Лебедь & Рак & Щука
- 14. Рыжий | Честный | Влюблённый
- 15. (Рыжий & Честный)|Влюблённый
- 16. (Солнце | Воздух) & Вода
- 17. Расположите коды запросов в порядке убывания
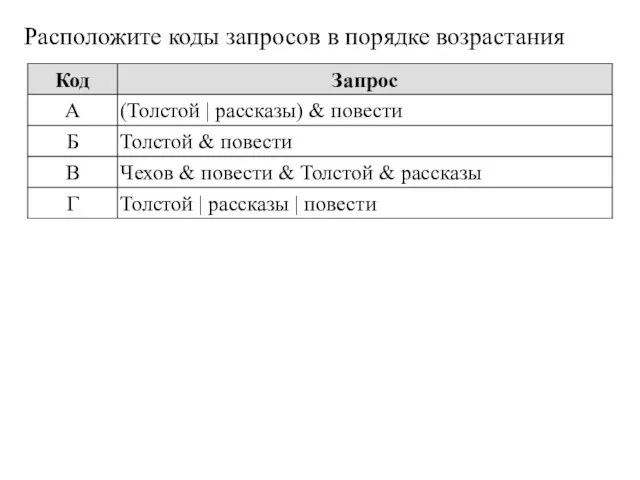
- 18. Расположите коды запросов в порядке возрастания
- 19. Расположите коды запросов в порядке возрастания
- 21. Скачать презентацию
















 Теорема Пифагора
Теорема Пифагора Вывод формулы Герона. Геометрия 8 класс
Вывод формулы Герона. Геометрия 8 класс Coordinate plane
Coordinate plane Шар и сфера
Шар и сфера Применение производной
Применение производной Помогают законы. 5 - 7 класс
Помогают законы. 5 - 7 класс Многоугольник
Многоугольник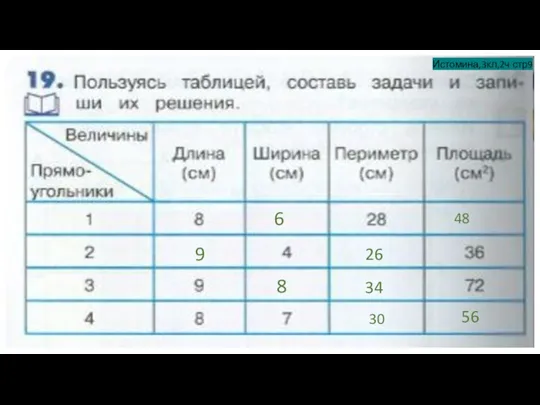 Величины. Составление задач
Величины. Составление задач Математика для дошкольников (средняя группа)
Математика для дошкольников (средняя группа) Кто живет под грибом
Кто живет под грибом Задачи для практики
Задачи для практики Введение в геометрию
Введение в геометрию Логическая задача. Способы решения
Логическая задача. Способы решения Презентация по математике "Величины. Объём" -
Презентация по математике "Величины. Объём" -  Презентация на тему Волейбол. Передача сверху
Презентация на тему Волейбол. Передача сверху  Алгебраическая дробь и её основное свойство. 7 класс
Алгебраическая дробь и её основное свойство. 7 класс Задачи на расстояния в пространстве
Задачи на расстояния в пространстве Как умножали египтяне
Как умножали египтяне Степень с натуральным показателем и его свойства
Степень с натуральным показателем и его свойства Презентация по математике "Число 7" -
Презентация по математике "Число 7" -  Симметрия в геометрии и в жизни
Симметрия в геометрии и в жизни Классификация функций
Классификация функций Математика
Математика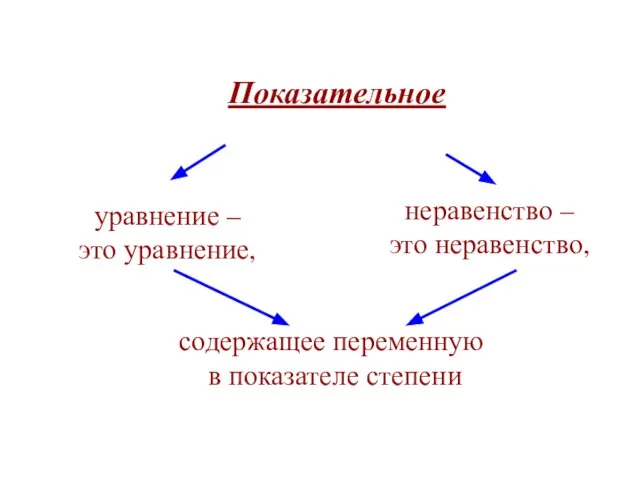 Показательное уравнение
Показательное уравнение Алгебра. Дроби. Сумма дробей
Алгебра. Дроби. Сумма дробей Координатная плоскость
Координатная плоскость Чётность и не чётность тригонометрических функций
Чётность и не чётность тригонометрических функций Числовая последовательность
Числовая последовательность