Содержание
- 2. Евдокс Книдский ок. 408 — ок. 355 год до н. э. Интегральное исчисление появилось во времена
- 3. Лейбниц Готфрид Вильгельм (1646-1716) Символ ∫ введен Лейбницем (1675 г.). Этот знак является изменением латинской буквы
- 4. Готфрид Вильгельм Лейбниц (1646—1716) Исаак Ньютон (1643 – 1727) Ньютон и Лейбниц открыли независимо друг от
- 5. Огюстен Луи Коши (1789 – 1857) Карл Теодор Вильгельм Вейерштрасс (1815 1897 ) Работы Коши и
- 6. В развитии интегрального исчисления приняли участие русские математики: М.В. Остроградский (1801 – 1862) В.Я. Буняковский (1804
- 7. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ Неопределенным интегралом от непрерывной функции f(x) на интервале (a; b) называют любую ее первообразную
- 8. Свойства интеграла
- 9. Свойства интеграла
- 10. Основные методы интегрирования Табличный. 2.Сведение к табличному преобразованием подынтегрального выражения в сумму или разность. 3.Интегрирование с
- 12. Скачать презентацию









 ГВЭ-9 по математике в 2020-2021 учебном году: структура, содержание КИМ, методика подготовки обучающихся
ГВЭ-9 по математике в 2020-2021 учебном году: структура, содержание КИМ, методика подготовки обучающихся Формулы. Урок 1
Формулы. Урок 1 Квадратные уравнения. Анаграммы
Квадратные уравнения. Анаграммы По следам теоремы Пифагора
По следам теоремы Пифагора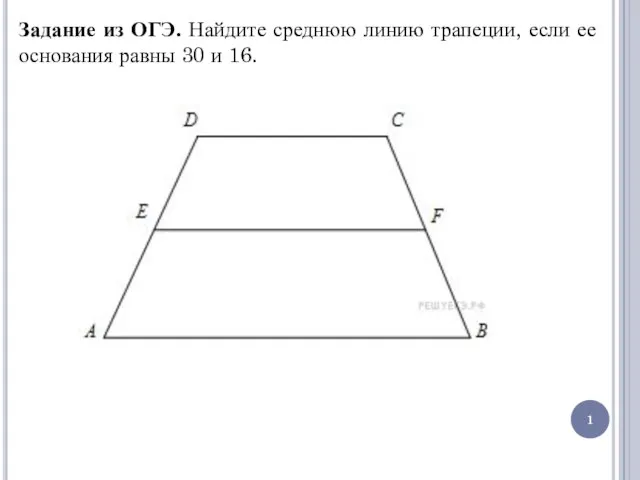 Прямоугольник. Ромб. Квадрат. Задание из ОГЭ
Прямоугольник. Ромб. Квадрат. Задание из ОГЭ Случаи вычитания 11-
Случаи вычитания 11- Круглые числа. Величина
Круглые числа. Величина Метод выделения квадрата
Метод выделения квадрата Многогранники: выпуклые призмы и антипризмы
Многогранники: выпуклые призмы и антипризмы Тригонометрические функции числового аргумента
Тригонометрические функции числового аргумента Прямоугольник
Прямоугольник Классификация средств измерений. Метрологические характеристики средств измерений
Классификация средств измерений. Метрологические характеристики средств измерений Перпендикулярность плоскостей
Перпендикулярность плоскостей Решение задач в целых числах
Решение задач в целых числах Современное школьное математическое образование
Современное школьное математическое образование Решение задач с помощью уравнений
Решение задач с помощью уравнений Геометрические фигуры
Геометрические фигуры Задачи на движение в противоположных направлениях
Задачи на движение в противоположных направлениях Математическая игра-раскраска Обезьянка
Математическая игра-раскраска Обезьянка Прямо-пропорциональные величины
Прямо-пропорциональные величины Прямой угол. Игра Гусеница-растеряша
Прямой угол. Игра Гусеница-растеряша Реляционная алгебра
Реляционная алгебра Старинные меры длины на Руси
Старинные меры длины на Руси Тригонометрические уравнения. Методы решения тригонометрических уравнений
Тригонометрические уравнения. Методы решения тригонометрических уравнений Основные формулы, схема исследования функции
Основные формулы, схема исследования функции Задачи на нахождение двух чисел по их сумме и разности
Задачи на нахождение двух чисел по их сумме и разности Векторы в пространстве
Векторы в пространстве Математика. 1 класс
Математика. 1 класс