Содержание
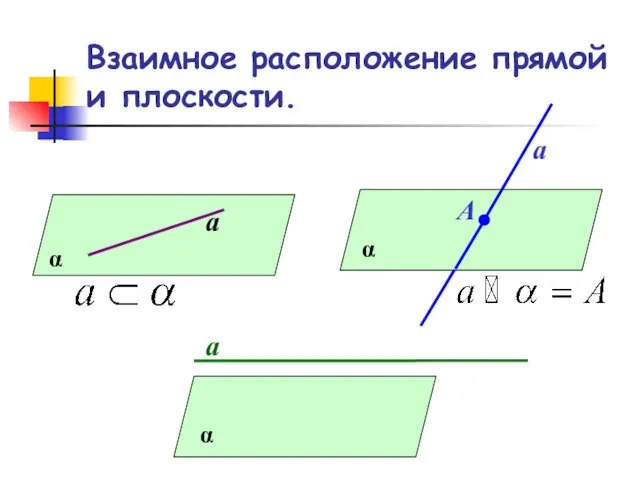
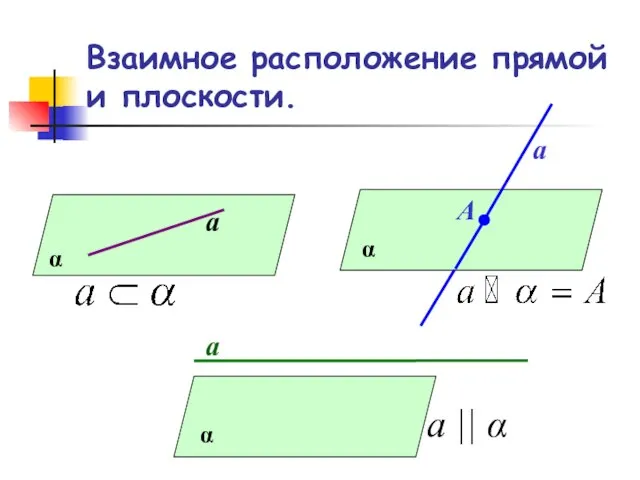
- 2. Взаимное расположение прямой и плоскости. α а α а А α а
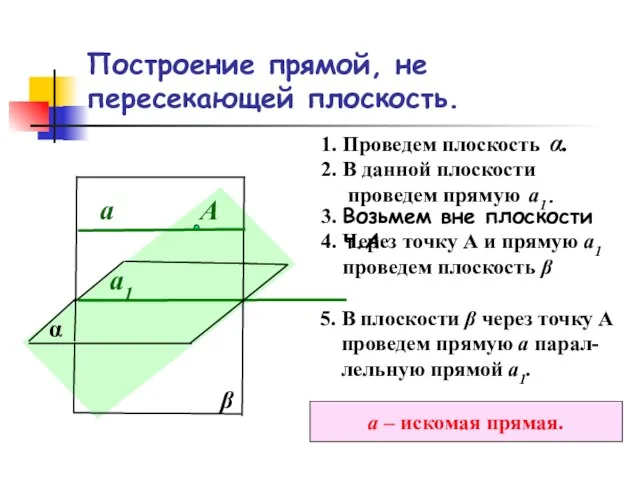
- 3. Построение прямой, не пересекающей плоскость. α 1. Проведем плоскость α. 2. В данной плоскости проведем прямую
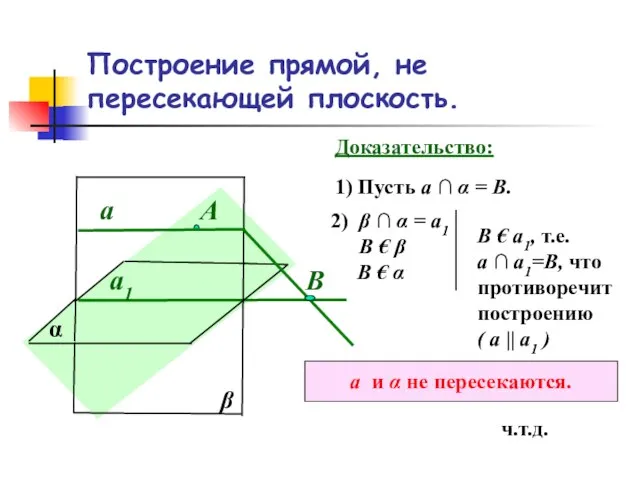
- 4. Построение прямой, не пересекающей плоскость. α а1 А β а Доказательство: 1) Пусть а ∩ α
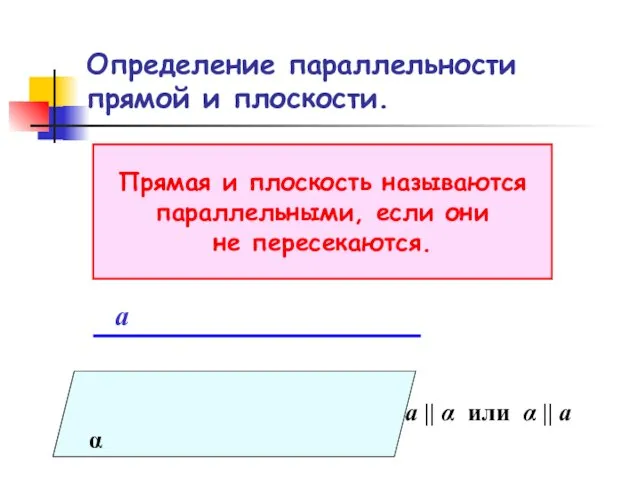
- 5. Определение параллельности прямой и плоскости. Прямая и плоскость называются параллельными, если они не пересекаются. α а
- 6. Взаимное расположение прямой и плоскости. α а α а А α а а || α
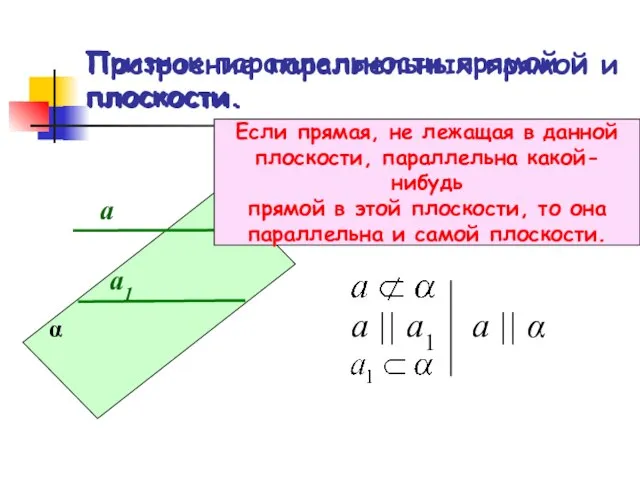
- 7. Построение параллельных прямой и плоскости. а1 а α а || а1 а || α Признак параллельности
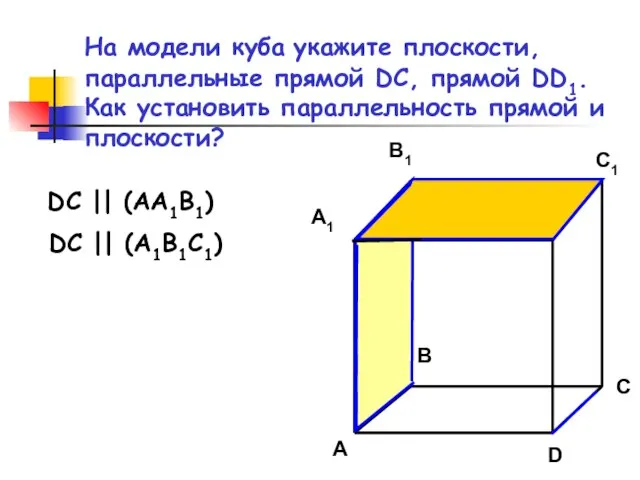
- 8. На модели куба укажите плоскости, параллельные прямой DC, прямой DD1. Как установить параллельность прямой и плоскости?
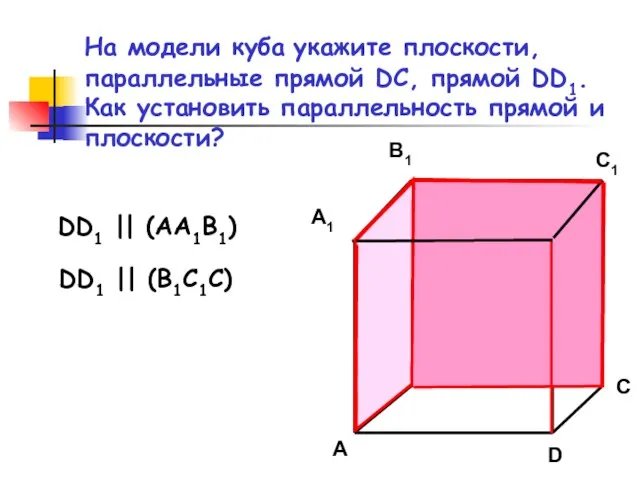
- 9. На модели куба укажите плоскости, параллельные прямой DC, прямой DD1. Как установить параллельность прямой и плоскости?
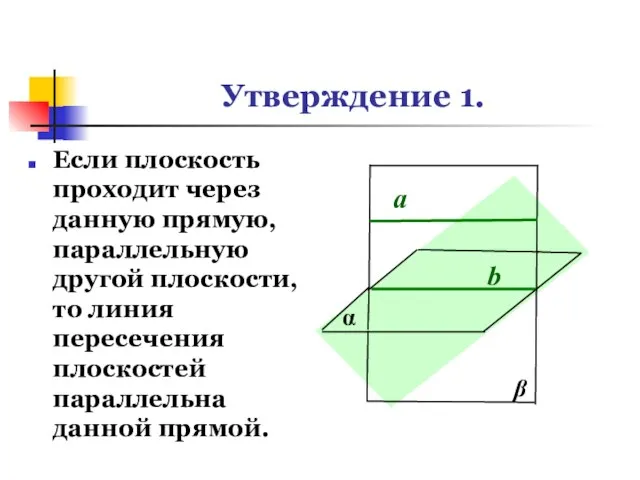
- 10. Утверждение 1. Если плоскость проходит через данную прямую, параллельную другой плоскости, то линия пересечения плоскостей параллельна
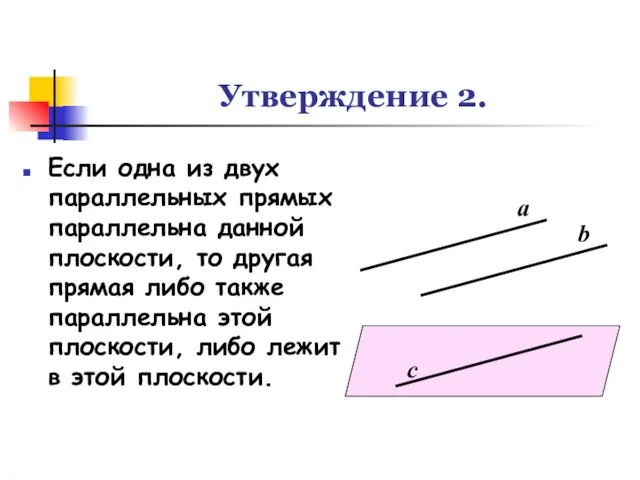
- 11. Утверждение 2. Если одна из двух параллельных прямых параллельна данной плоскости, то другая прямая либо также
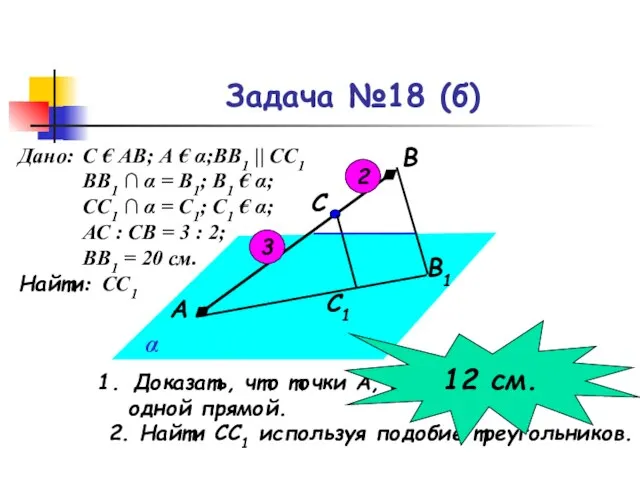
- 12. Задача №18 (б) С1 В1 С В А α Доказать, что точки А, В1, С1 лежат
- 13. Домашнее задание: П. 6; №№ 18(а); 26; 28.
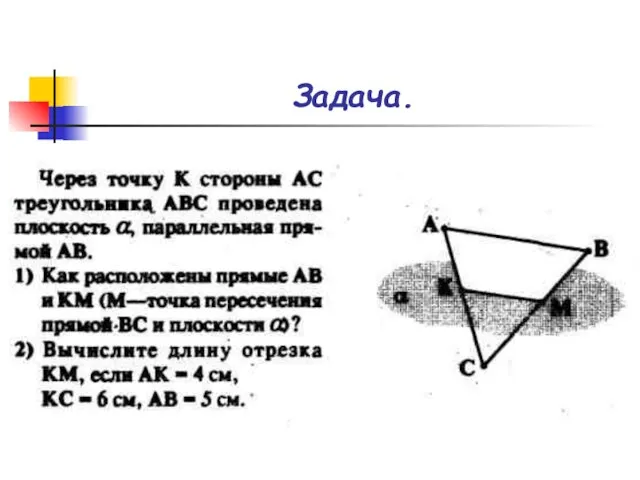
- 14. Задача.
- 16. Скачать презентацию

 Разложение разности квадратов на множители
Разложение разности квадратов на множители слож и выч вект умножение на число
слож и выч вект умножение на число Решение тригонометрических уравнений
Решение тригонометрических уравнений Последовательности. Золотое сечение
Последовательности. Золотое сечение Анализ геометрической формы предмета
Анализ геометрической формы предмета Шар. Объём шара
Шар. Объём шара Презентация на тему Дифференциальные уравнения первого порядка
Презентация на тему Дифференциальные уравнения первого порядка  Таблица умножения. Анимированная сорбонка
Таблица умножения. Анимированная сорбонка Урок алгебры. Свойства корня n -ой степени
Урок алгебры. Свойства корня n -ой степени Определение двойного интеграла
Определение двойного интеграла Деление на натуральное число и деление на десятичную дробь
Деление на натуральное число и деление на десятичную дробь Построение сечений многогранников
Построение сечений многогранников Системы уравнений
Системы уравнений Литр. Задачи
Литр. Задачи Статические таблицы
Статические таблицы Округление чисел
Округление чисел Индивидуальные задания. Урок 15
Индивидуальные задания. Урок 15 Показательные уравнения, сводящиеся к квадратным
Показательные уравнения, сводящиеся к квадратным Векторы. Линейные операции над векторами. Разложение вектора по базису
Векторы. Линейные операции над векторами. Разложение вектора по базису Урок математики. Повторение изученного
Урок математики. Повторение изученного Элементы теории множеств
Элементы теории множеств Презентация на тему Золотое сечение
Презентация на тему Золотое сечение  Смешанные числа (часть 1)
Смешанные числа (часть 1) Понятие области
Понятие области Вычисление неопределенного интеграла
Вычисление неопределенного интеграла Нахождение дроби от числа
Нахождение дроби от числа Готовимся к ОГЭ по математике
Готовимся к ОГЭ по математике Сумма углов треугольника
Сумма углов треугольника