Содержание
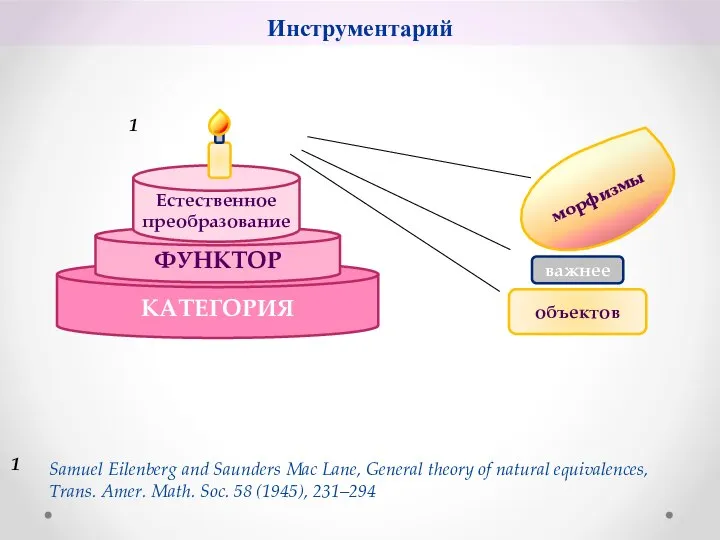
- 2. КАТЕГОРИЯ ФУНКТОР Естественное преобразование морфизмы важнее объектов 1 Samuel Eilenberg and Saunders Mac Lane, General theory
- 3. Пример коммутативной диаграммы Базовые понятия теории категорий
- 4. Категория HTop Пример Базовые понятия теории категорий
- 5. Базовые понятия теории категорий
- 6. M → Z(M) Замкнутое ориентированное (n-1)-многообразие Векторное пространство над полем F Ориентированный кобордизм Линейное отображение между
- 7. ′B M0 M1 Категория nCob ′B B M1 M0 d
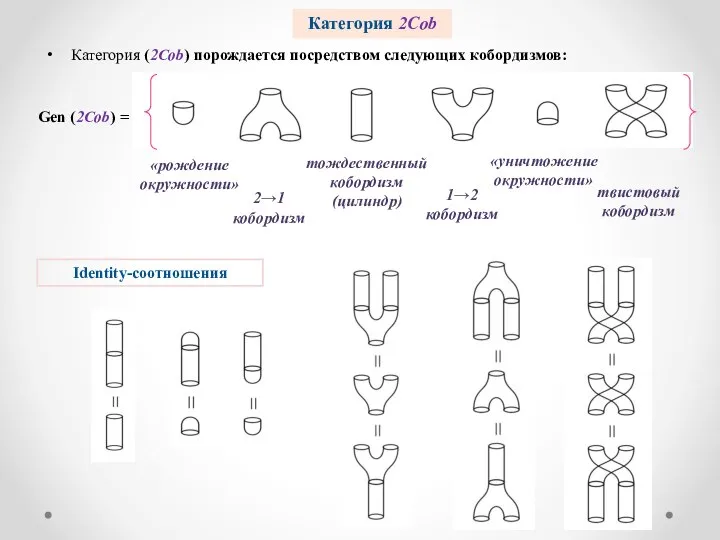
- 8. Категория (2Cob) порождается посредством следующих кобордизмов: Категория 2Cob «рождение окружности» 2→1 кобордизм тождественный кобордизм (цилиндр) твистовый
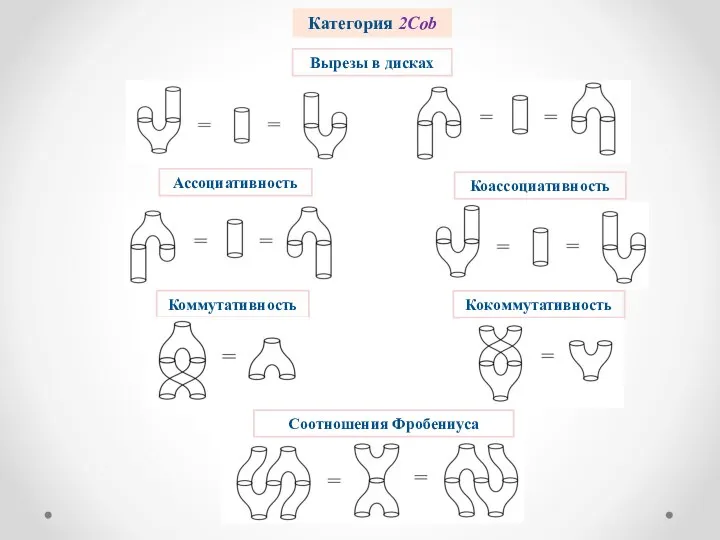
- 9. Категория 2Cob Вырезы в дисках Коммутативность Кокоммутативность Соотношения Фробениуса Ассоциативность Коассоциативность
- 10. F-алгебра A – F-векторное пространство, наделенное F-линейными отображениями Фробениусовы алгебры умножением µ: A ⊗ A →
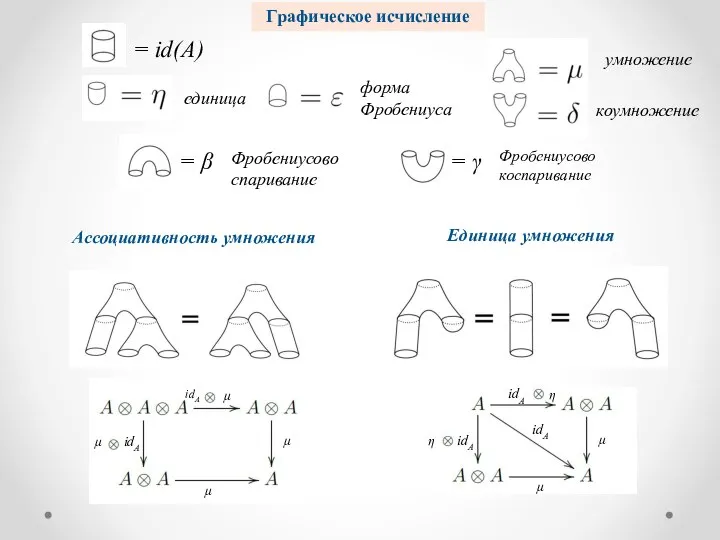
- 11. Графическое исчисление = id(A) единица форма Фробениуса умножение коумножение Фробениусово спаривание Фробениусово коспаривание = β =
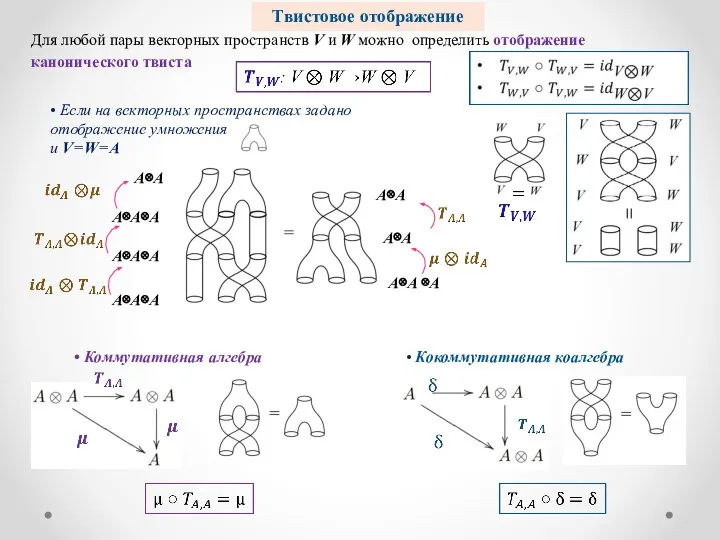
- 12. Твистовое отображение Для любой пары векторных пространств V и W можно определить отображение канонического твиста A⊗A
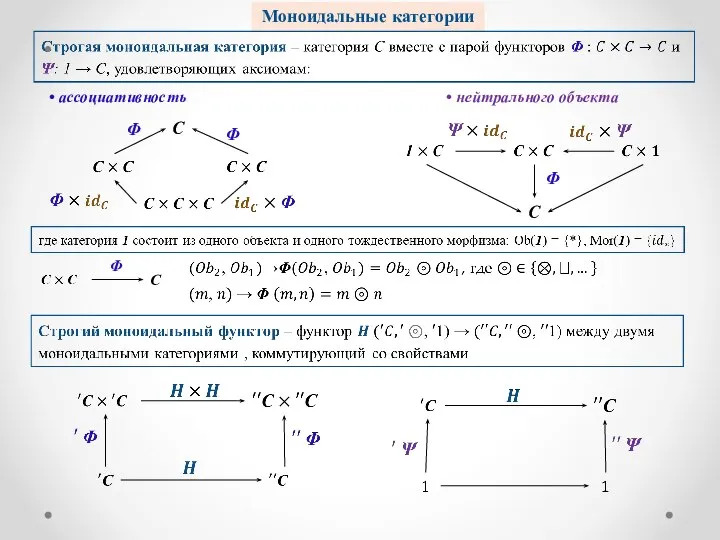
- 13. Моноидальные категории • ассоциативность • нейтрального объекта C Φ
- 14. Симметричные моноидальные категории : : диаграмма коммутативна справедливо
- 15. Примеры моноидальных категорий Нестрогой Строгой Моноидальные структуры
- 16. Топологическая квантовая теория поля (ТКТП) Соотношения категории 2Cob переходят в аксиомы коммутативной Фробениусовой алгебры Имеет место
- 18. Скачать презентацию









 Стохастические процессы
Стохастические процессы Презентация на тему Графическое решение уравнений
Презентация на тему Графическое решение уравнений  Старинные меры массы и длины
Старинные меры массы и длины Комплексные числа. Все формы
Комплексные числа. Все формы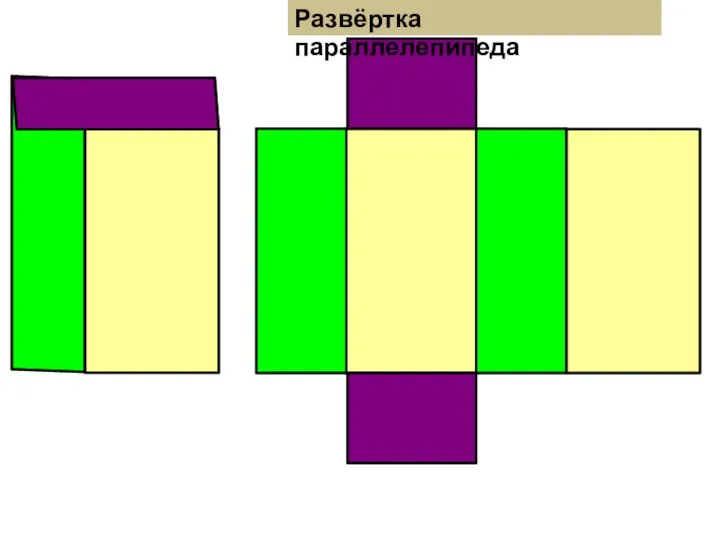 Развёртка параллелепипеда, куба, треугольной и четырёхугольной пирамиды. 5 класс
Развёртка параллелепипеда, куба, треугольной и четырёхугольной пирамиды. 5 класс Тригонометрические уравнения
Тригонометрические уравнения Квадратичная функция и её график. Методические материалы урока
Квадратичная функция и её график. Методические материалы урока Презентация на тему Объём многогранника
Презентация на тему Объём многогранника  Сближение меридианов. Международное геомагнитное аналитическое поле IGRF
Сближение меридианов. Международное геомагнитное аналитическое поле IGRF Задачи про форматы листов. Решение практико-ориентированных задач
Задачи про форматы листов. Решение практико-ориентированных задач Метод обратной матрицы решения систем линейных уравнений
Метод обратной матрицы решения систем линейных уравнений Методика работы с задачей на круговое движение
Методика работы с задачей на круговое движение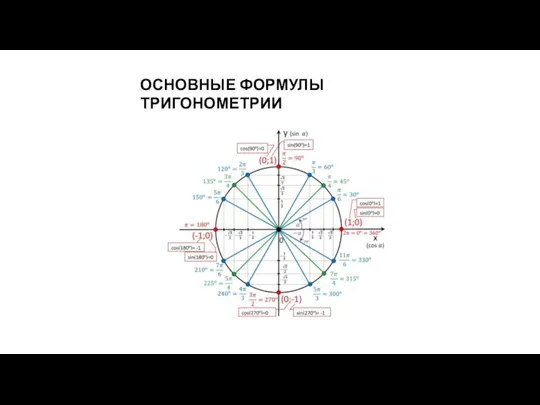 Основные формулы тригонометрии
Основные формулы тригонометрии Деление обыкновенных дробей
Деление обыкновенных дробей 7490_md_sin_cos_tg_0
7490_md_sin_cos_tg_0 Пирамида и её элементы. Правильная пирамида
Пирамида и её элементы. Правильная пирамида Математика вокруг нас
Математика вокруг нас Время. Единицы времени
Время. Единицы времени Первый замечательный предел
Первый замечательный предел Математика ЕГЭ. Углы и прямые
Математика ЕГЭ. Углы и прямые Линейная функция и её график
Линейная функция и её график Теория вероятностей в задачах ЕГЭ
Теория вероятностей в задачах ЕГЭ Основы логистики
Основы логистики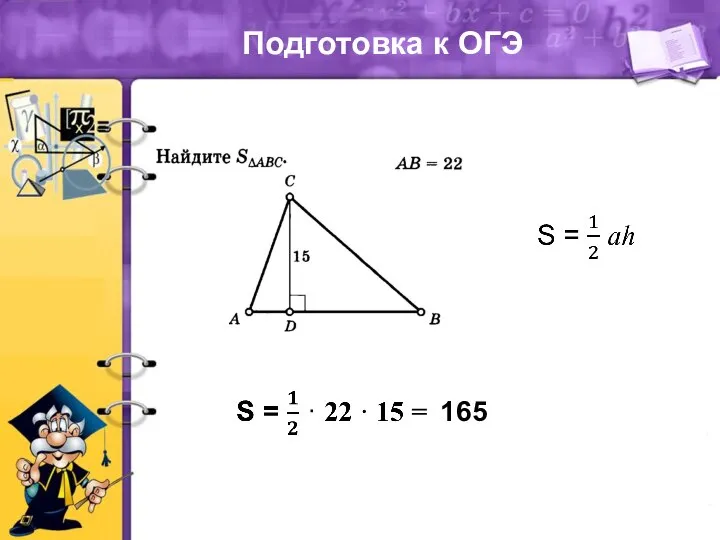 Теорема площади треугольника. Подготовка к ОГЭ
Теорема площади треугольника. Подготовка к ОГЭ Прямоугольник. Геометрия 8 класс
Прямоугольник. Геометрия 8 класс Логарифмические выражения
Логарифмические выражения Презентация по математике "Применение приёмов интерактивного обучения на уроках математики" -
Презентация по математике "Применение приёмов интерактивного обучения на уроках математики" -  Презентация на тему Метод координат в пространстве
Презентация на тему Метод координат в пространстве