Объем прямоугольного параллелепипеда

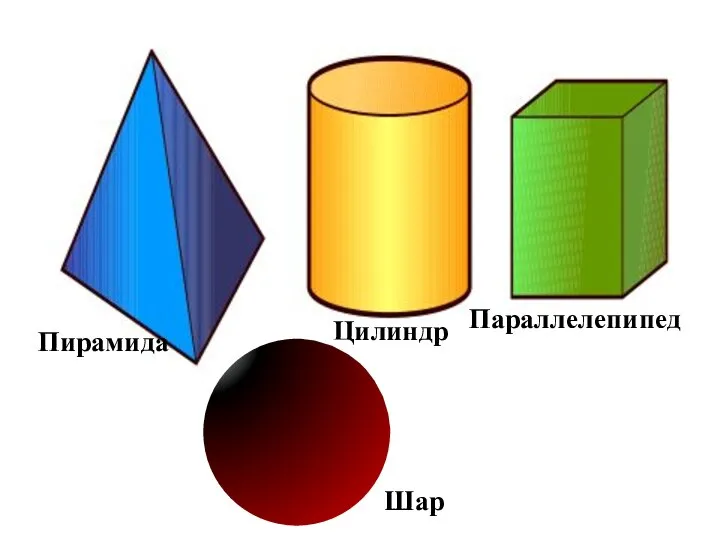
Пирамида
Цилиндр
Параллелепипед
Шар

Предметы в жизни, имеющие форму параллелепипеда.

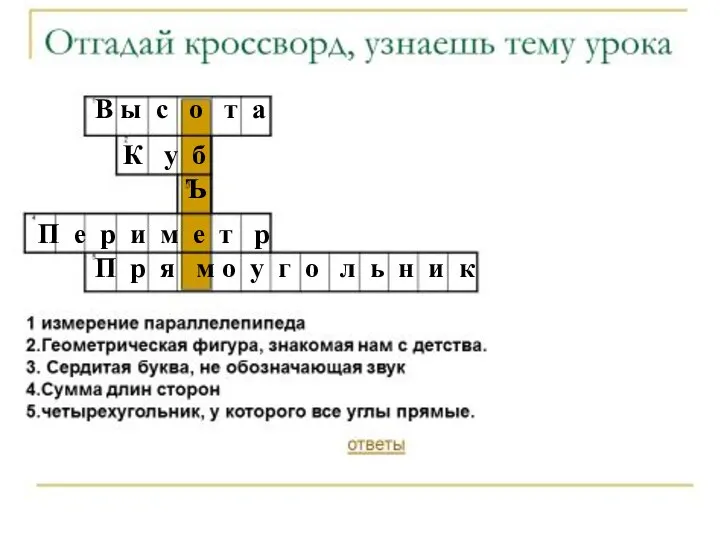
В ы с о т а
К у б
Ъ
П е р и м е т р
П р я м о у г о л ь н и к

Классная работа.
Объем прямоугольного параллелепипеда.

Что такое объем?
Объём — количественная характеристика пространства, занимаемого телом или веществом.

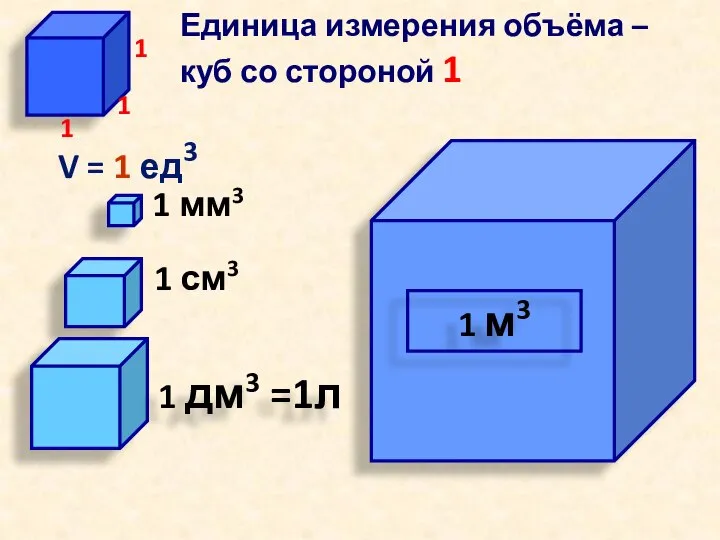
Единица измерения объёма – куб со стороной 1
1 см3
V = 1 ед3
1 дм3 =1л
1 мм3

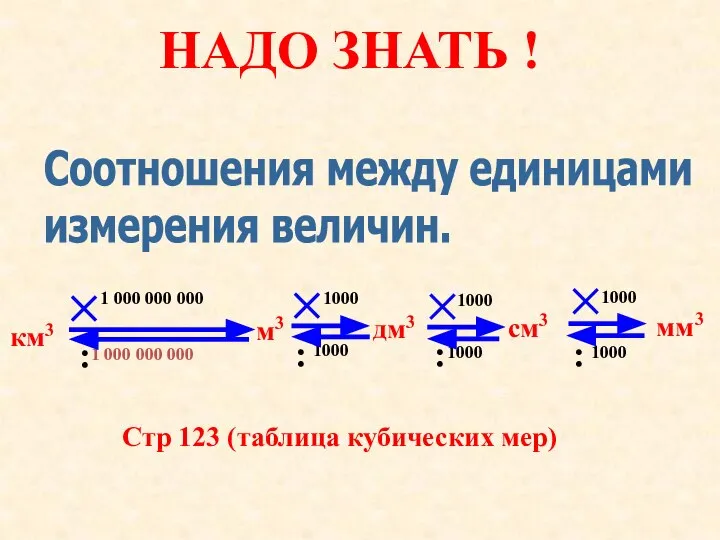
Соотношения между единицами
измерения величин.
1000
м3
мм3
см3
км3
дм3
1000
1000
1 000 000 000
1 000 000 000
:
НАДО ЗНАТЬ !
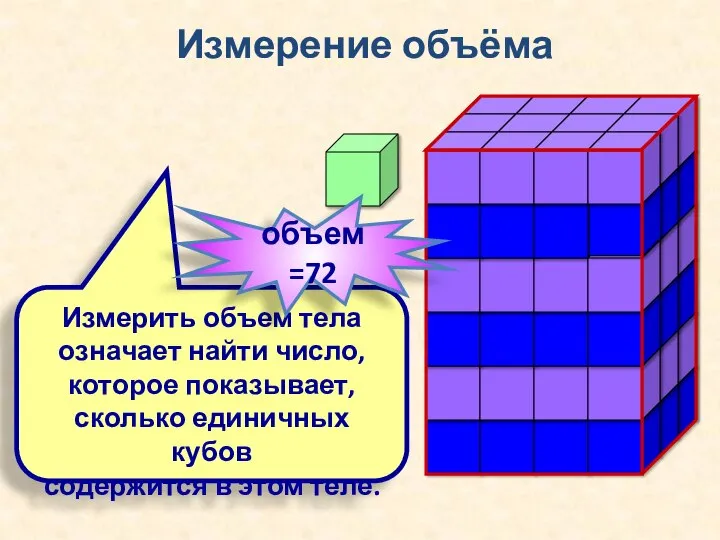
Стр 123 (таблица кубических мер)

Измерение объёма
Измерить объем тела означает найти число, которое показывает,
сколько единичных кубов
содержится в этом теле.
объем =72

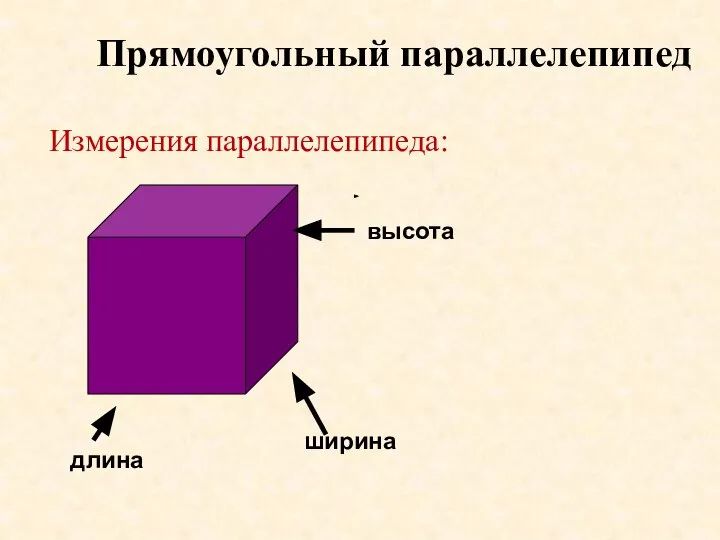
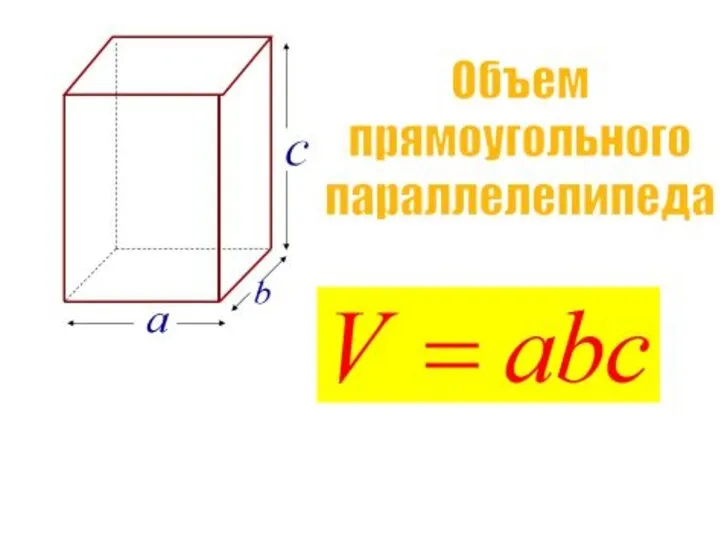
Прямоугольный параллелепипед
Измерения параллелепипеда:
длина
ширина
высота

а
b
c
a – длина, b – ширина, с – высота
Объем прямоугольного параллелепипеда.
V= abc
Объем прямоугольного
параллелепипеда равен произведению
трех его измерений.

Высота кабинета 4 м, ширина 7 м, и длина 8 м. Сколько кубических метров воздуха находится в кабинете?

Высота кабинета 4 м, ширина 7 м. и длина 8 м. Сколько кубических метров воздуха находится в комнате?
Решение:
V = a · b · с;
V=8м · 7м· 4м = 224 м3 воздуха находится в комнате.
Ответ : 224 м3
Краткая запись:
Высота кабинета – 4м
Ширина кабинета – 7м
Длина кабинета – 8м
Объём - ?

Домашнее задание.
Стр 124 № 624 1)