Двугранный угол

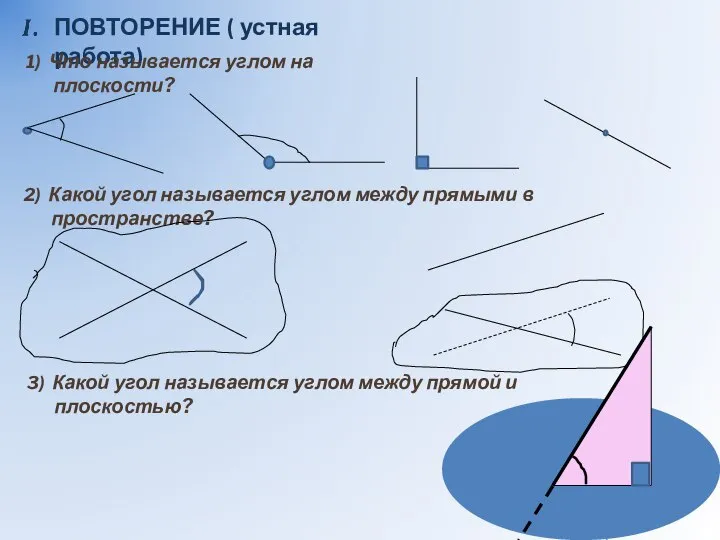
ПОВТОРЕНИЕ ( устная работа)
1) Что называется углом на плоскости?
2) Какой угол называется углом между прямыми в пространстве?
3) Какой угол называется углом между прямой и плоскостью?

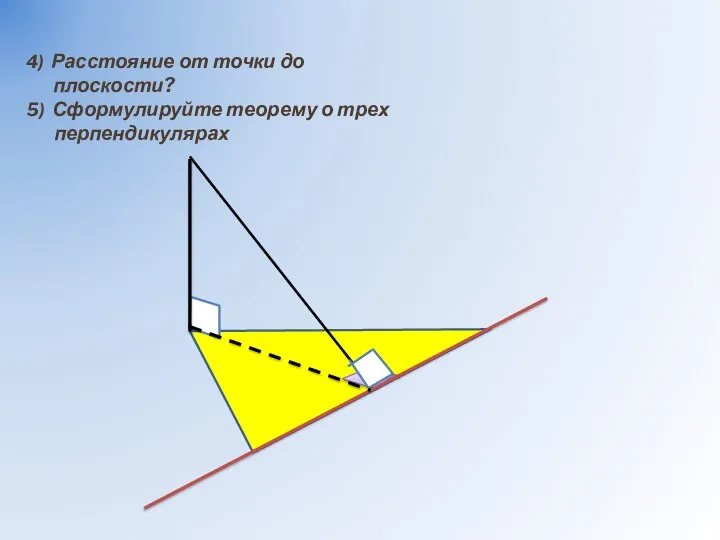
4) Расстояние от точки до плоскости?
5) Сформулируйте теорему о трех перпендикулярах

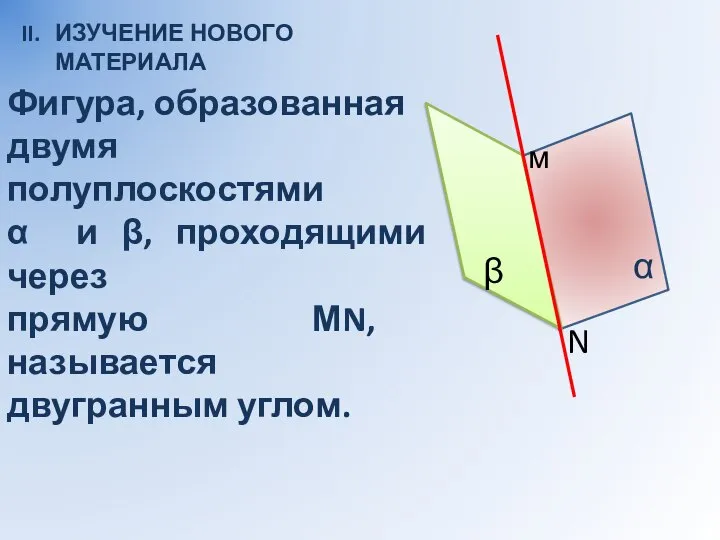
II.
ИЗУЧЕНИЕ НОВОГО МАТЕРИАЛА
α
β
м
N
Фигура, образованная
двумя полуплоскостями
α и β, проходящими через
прямую МN, называется
двугранным углом.

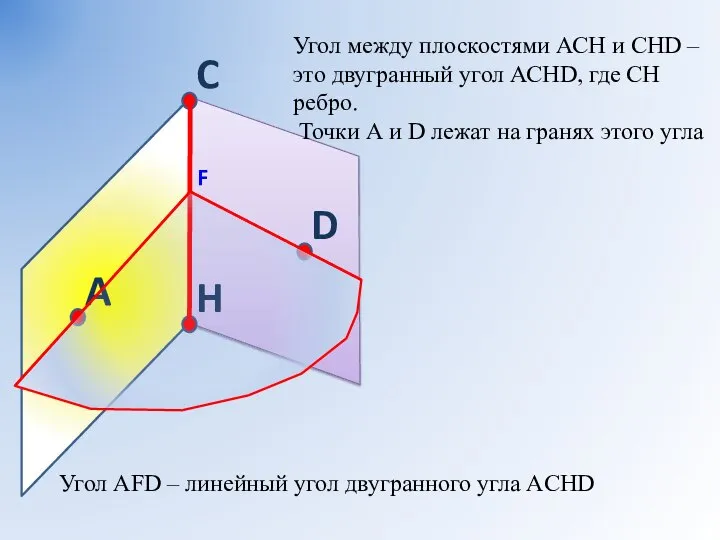
Угол между плоскостями АСН и СНD – это двугранный угол АСНD, где СН ребро.
Точки А и D лежат на гранях этого угла
F
Угол AFD – линейный угол двугранного угла АCHD

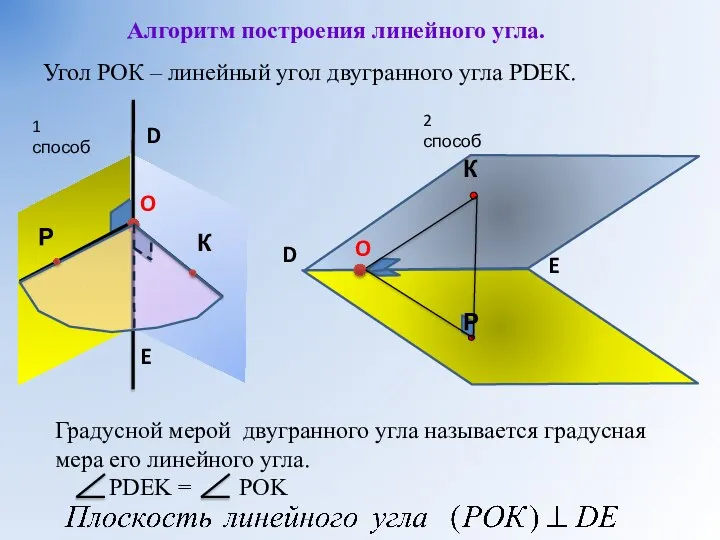
Угол РОК – линейный угол двугранного угла РDEК.
D
E
Градусной мерой двугранного угла называется градусная мера его линейного угла.
PDEK = POK
Алгоритм построения линейного угла.
D
E
O
1 способ
2 способ

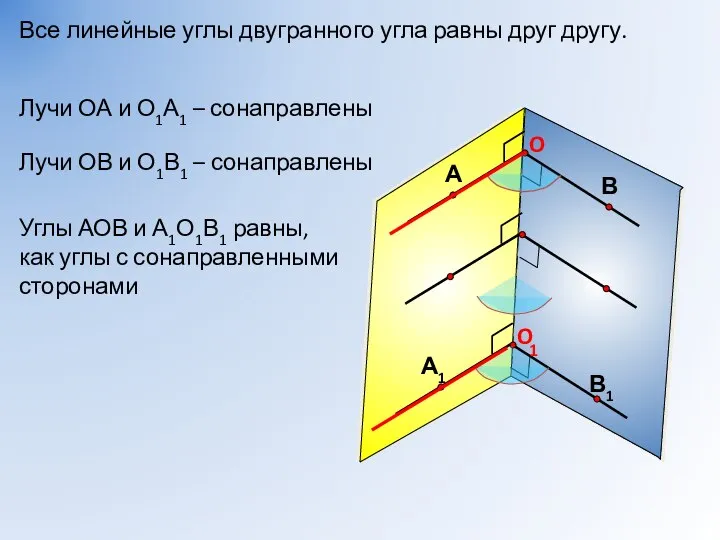
Все линейные углы двугранного угла равны друг другу.
1
Лучи ОА и О1А1 – сонаправлены
Лучи ОВ и О1В1 – сонаправлены
Углы АОВ и А1О1В1 равны,
как углы с сонаправленными сторонами

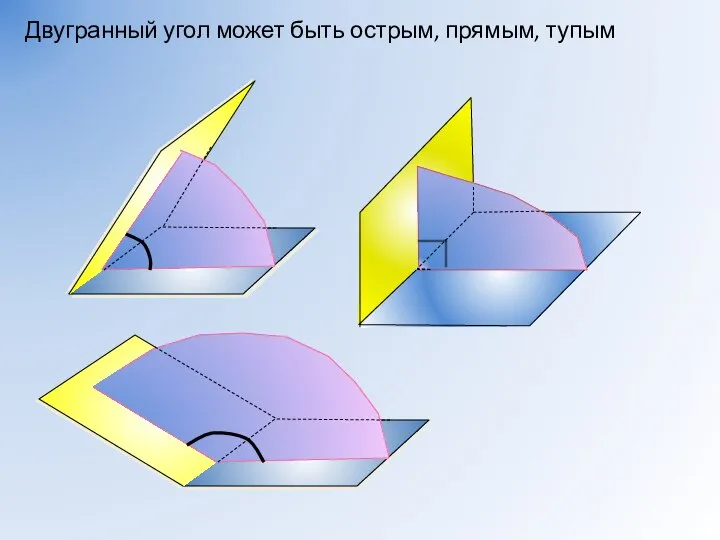
Двугранный угол может быть острым, прямым, тупым

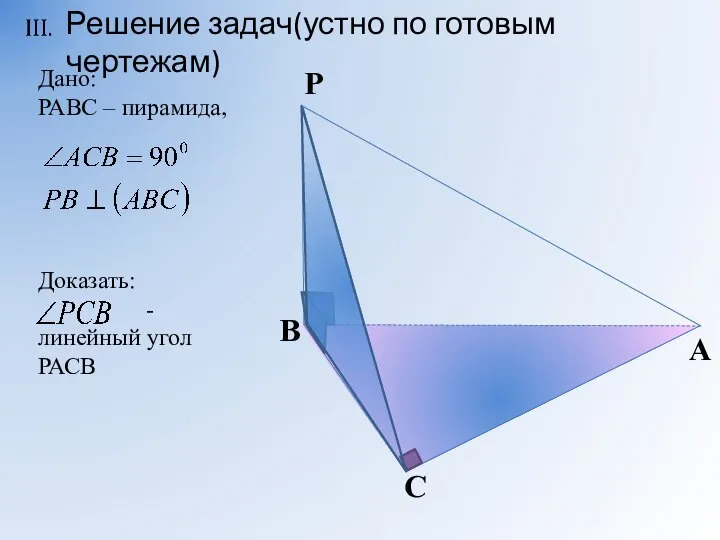
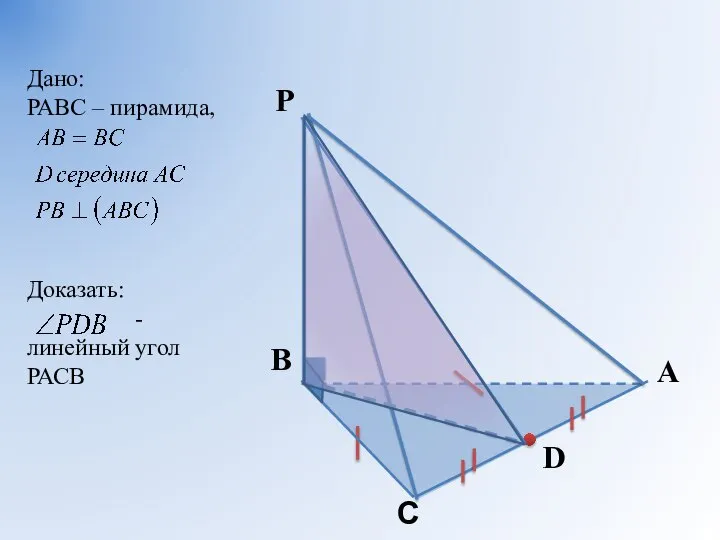
Дано:
РАВС – пирамида,
Доказать:
- линейный угол РАСВ
Решение задач(устно по готовым чертежам)

Дано:
РАВС – пирамида,
Доказать:
- линейный угол РАСВ

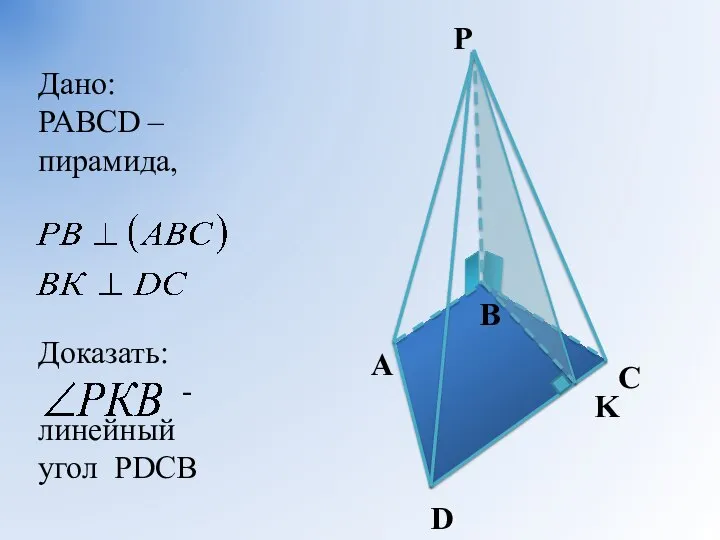
A
B
C
D
P
K
Дано:
РАВСD – пирамида,
Доказать:
- линейный угол РDСВ

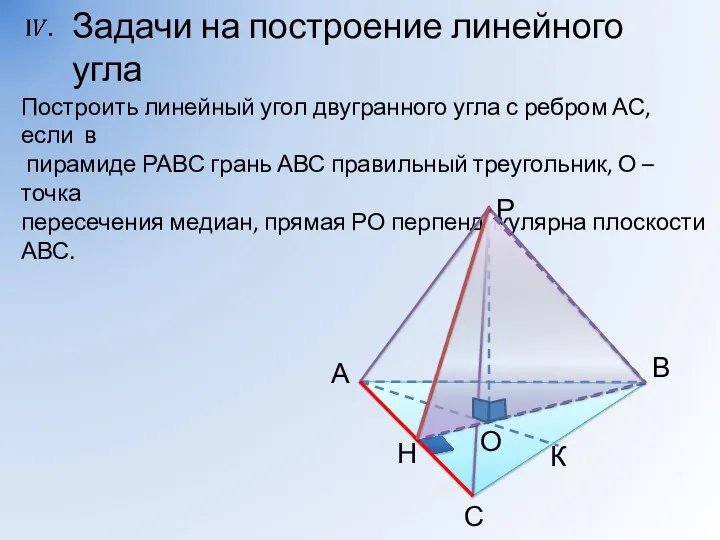
Построить линейный угол двугранного угла с ребром АС, если в
пирамиде РАВС грань АВС правильный треугольник, О – точка
пересечения медиан, прямая РО перпендикулярна плоскости АВС.
А
В
С
К
Н
О
Р
Задачи на построение линейного угла

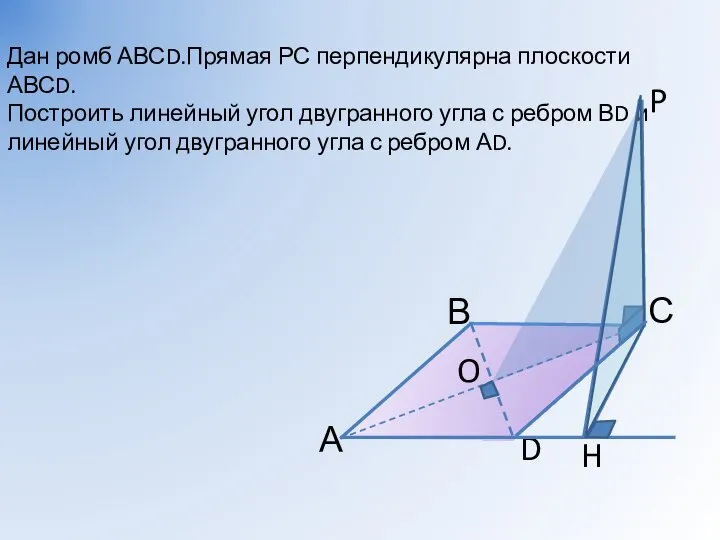
Дан ромб АВСD.Прямая РС перпендикулярна плоскости АВСD.
Построить линейный угол двугранного угла с ребром ВD и
линейный угол двугранного угла с ребром АD.
H
O

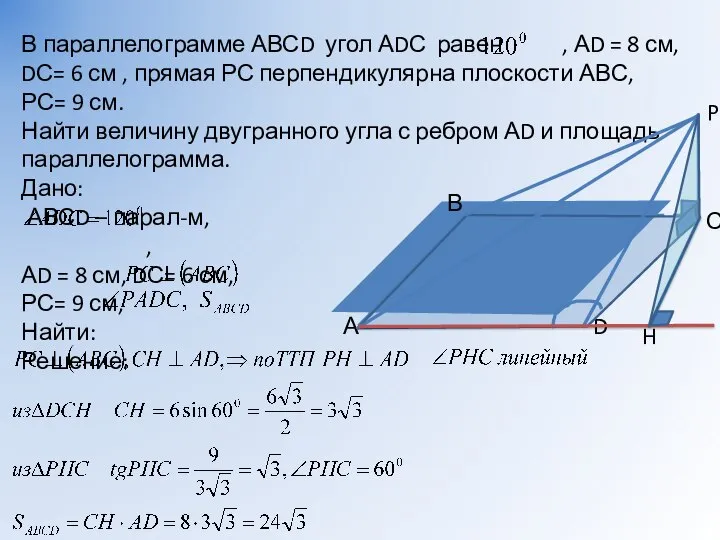
В параллелограмме АВСD угол АDС равен , АD = 8 см,
DС= 6 см , прямая РС перпендикулярна плоскости АВС, РС= 9 см.
Найти величину двугранного угла с ребром АD и площадь
параллелограмма.
Дано:
АВСD – парал-м,
,
АD = 8 см, DС= 6 см,
РС= 9 см,
Найти:
Решение:
H

Домашнее задание: п.22 №168,171