Содержание
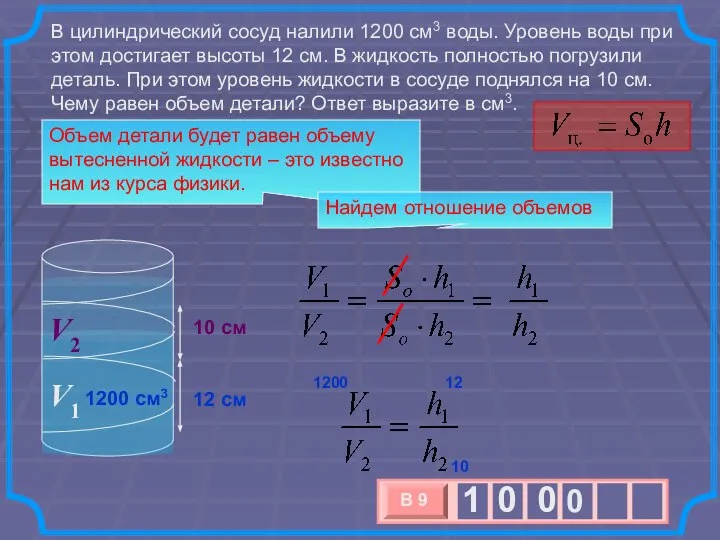
- 2. В цилиндрический сосуд налили 1200 см3 воды. Уровень воды при этом достигает высоты 12 см. В
- 3. В цилиндрическом сосуде уровень жидкости достигает 27 см. На какой высоте будет находиться уровень жидкости, если
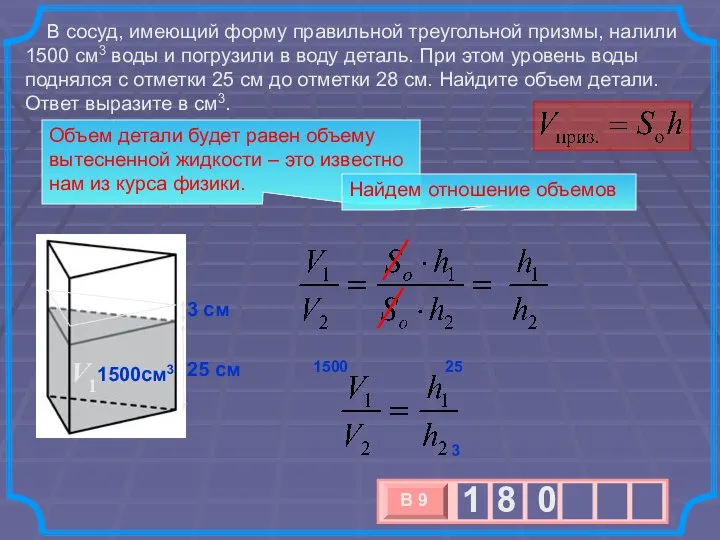
- 4. В сосуд, имеющий форму правильной треугольной призмы, налили 1500 см3 воды и погрузили в воду деталь.
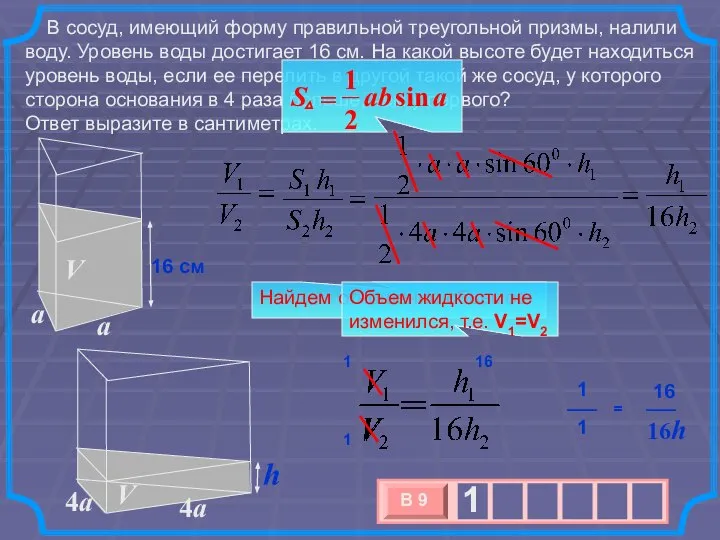
- 5. В сосуд, имеющий форму правильной треугольной призмы, налили воду. Уровень воды достигает 16 см. На какой
- 6. В основании прямой призмы лежит прямоугольный треугольник с катетами 6 и 8. Боковые ребра равны .
- 7. В основании прямой призмы лежит квадрат со стороной 2. Боковые ребра равны . Найдите объем цилиндра,
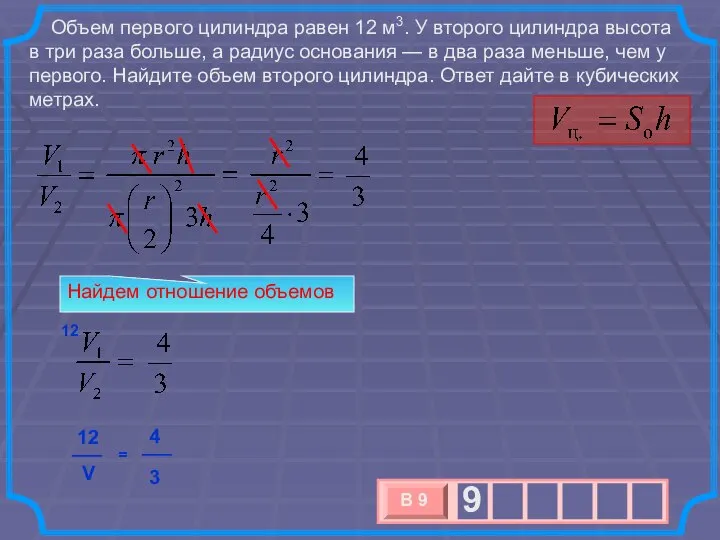
- 8. Объем первого цилиндра равен 12 м3. У второго цилиндра высота в три раза больше, а радиус
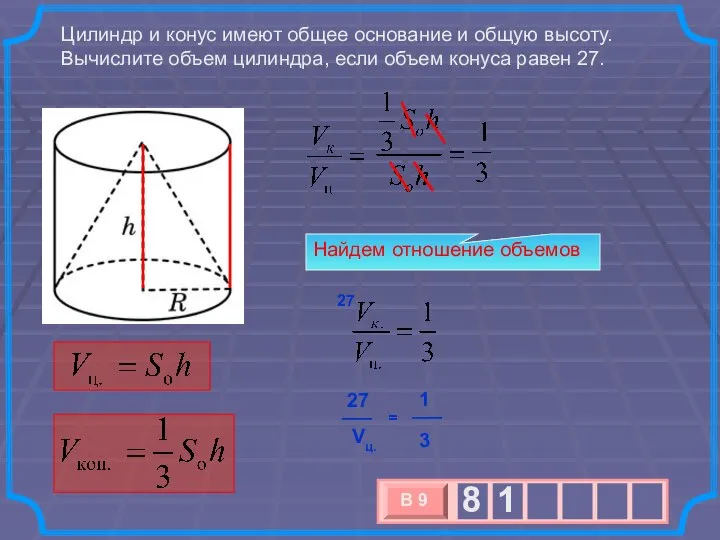
- 9. Цилиндр и конус имеют общее основание и общую высоту. Вычислите объем цилиндра, если объем конуса равен
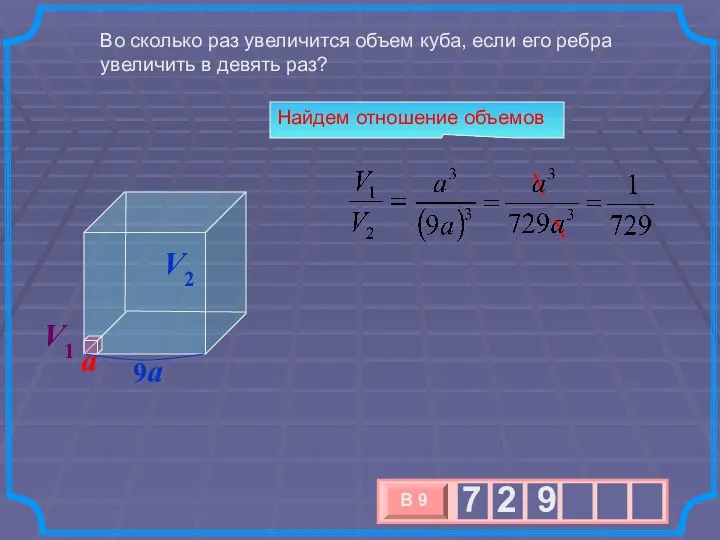
- 10. Во сколько раз увеличится объем куба, если его ребра увеличить в девять раз? Найдем отношение объемов
- 11. Диагональ куба равна . Найдите его объем. a a a
- 12. Объем куба равен 24 . Найдите его диагональ. a a a 8 3 ⋅
- 13. x 4 Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2, 4. Диагональ параллелепипеда равна
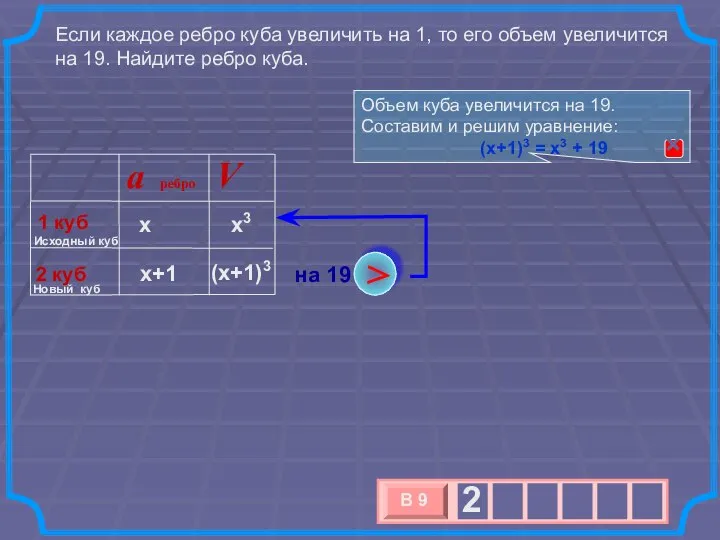
- 14. Если каждое ребро куба увеличить на 1, то его объем увеличится на 19. Найдите ребро куба.
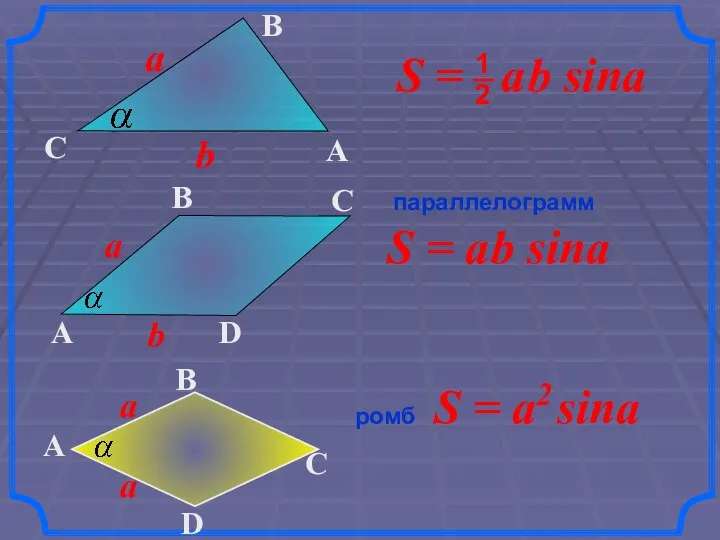
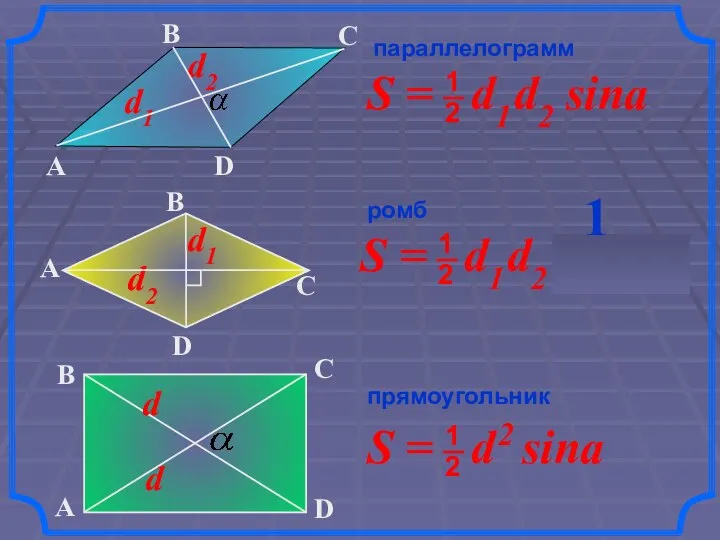
- 15. S = a2 sina параллелограмм ромб S = a b sina
- 16. параллелограмм ромб прямоугольник 1
- 17. Найдите объем правильной шестиугольной призмы, стороны основания которой равны 9, а боковые ребра равны . 9
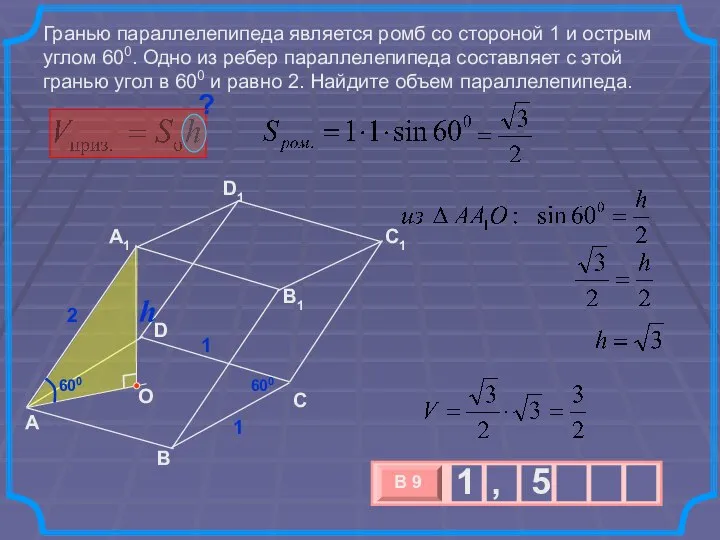
- 18. Гранью параллелепипеда является ромб со стороной 1 и острым углом 600. Одно из ребер параллелепипеда составляет
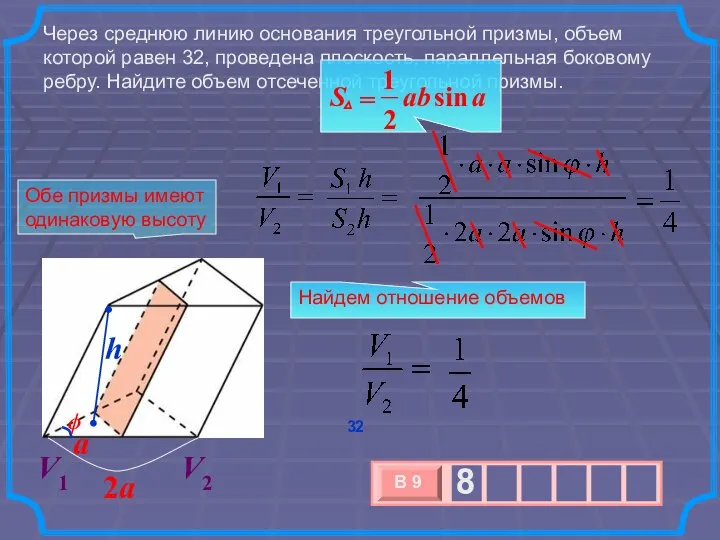
- 19. Через среднюю линию основания треугольной призмы, объем которой равен 32, проведена плоскость, параллельная боковому ребру. Найдите
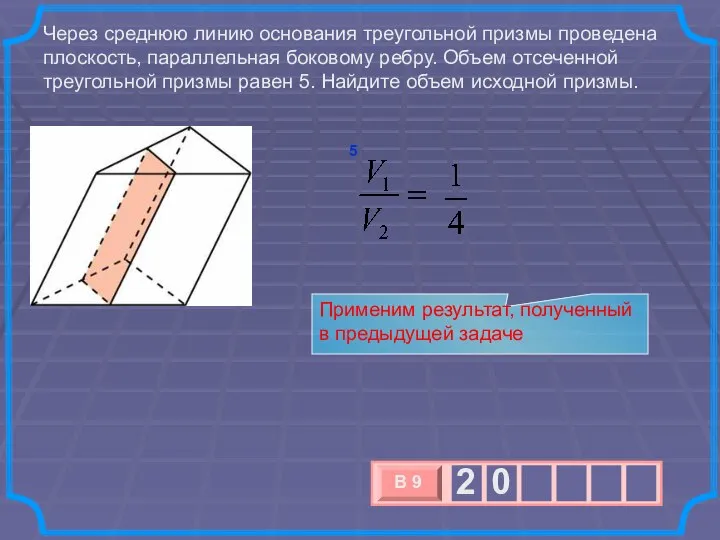
- 20. Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Объем отсеченной треугольной призмы равен
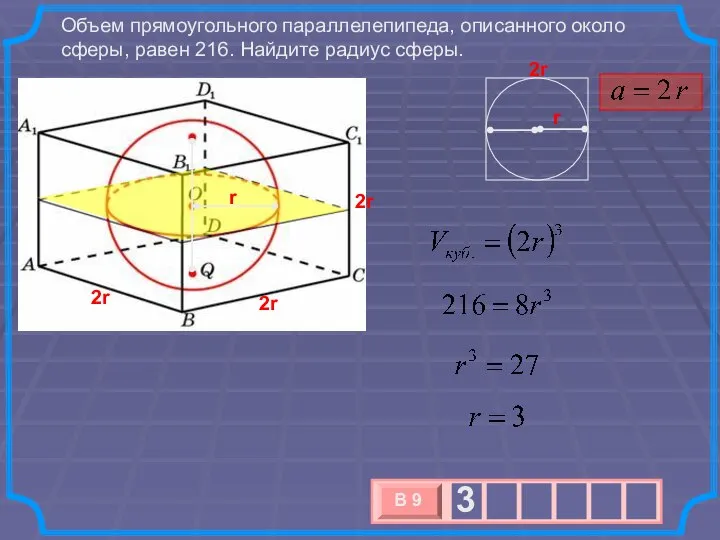
- 21. Объем прямоугольного параллелепипеда, описанного около сферы, равен 216. Найдите радиус сферы. r
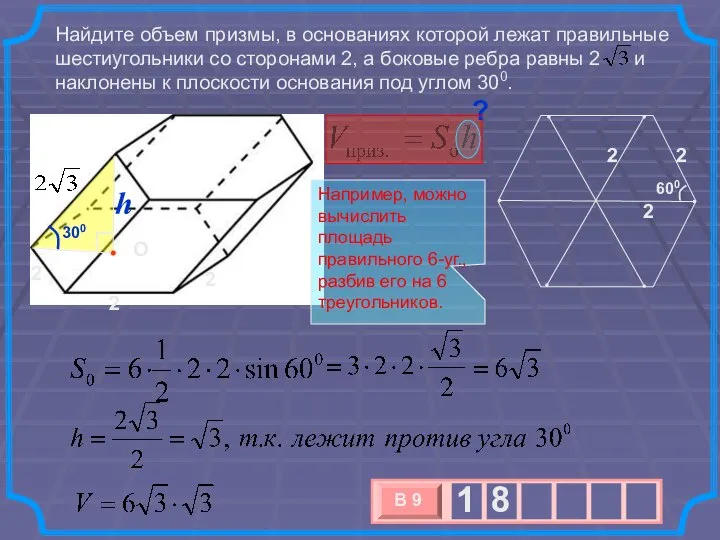
- 22. Найдите объем призмы, в основаниях которой лежат правильные шестиугольники со сторонами 2, а боковые ребра равны
- 23. Диагональ прямоугольного параллелепипеда равна и образует углы 300, 300 и 450 с плоскостями граней параллелепипеда. Найдите
- 25. Скачать презентацию








 Теория игр
Теория игр Презентация на тему Угол. Прямой и развернутый угол
Презентация на тему Угол. Прямой и развернутый угол  Построение графика квадратичной функции у=ах2+bx+c, a не равно 0
Построение графика квадратичной функции у=ах2+bx+c, a не равно 0 Основные формулы для Огэ по математике
Основные формулы для Огэ по математике Презентация на тему Вписанные углы
Презентация на тему Вписанные углы  Подготовка к ГИА по математике. Задания 14
Подготовка к ГИА по математике. Задания 14 Понятие вектора
Понятие вектора Формулы и функции в Excel
Формулы и функции в Excel Презентация на тему Задания В-9 ЕГЭ-2010
Презентация на тему Задания В-9 ЕГЭ-2010  Движение подводной лодки. Расчетная работа
Движение подводной лодки. Расчетная работа Для чего нужна математика?
Для чего нужна математика?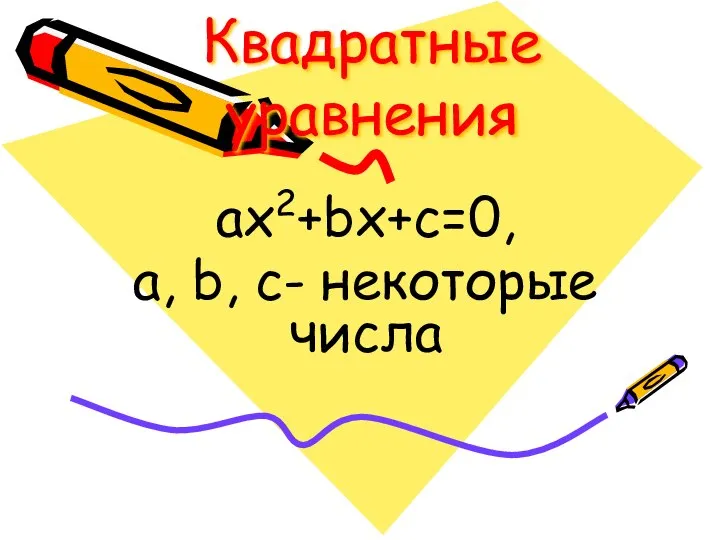 Квадратные уравнения ax +bx+c=0
Квадратные уравнения ax +bx+c=0 Куб
Куб Генеалогическое древо семьи Бернулли
Генеалогическое древо семьи Бернулли Опрос общественного мнения. Повторение действий с дробями
Опрос общественного мнения. Повторение действий с дробями Понятие смешанной дроби
Понятие смешанной дроби Подготовка к контрольной работе №4. 5 класс
Подготовка к контрольной работе №4. 5 класс Отделение математических наук РАН
Отделение математических наук РАН Функции и графики. Элективный курс по математике. 9 класс
Функции и графики. Элективный курс по математике. 9 класс Математика. 1 класс
Математика. 1 класс Ряд Тейлора функции многих переменных. Лекция 19
Ряд Тейлора функции многих переменных. Лекция 19 Нормальные формы булевых функций
Нормальные формы булевых функций Конус
Конус Презентация на тему ЗАДАЧИ НА ЧАСТИ
Презентация на тему ЗАДАЧИ НА ЧАСТИ  Поверхности второго порядка
Поверхности второго порядка Математический хоккей
Математический хоккей Презентация на тему Лист Мебиуса
Презентация на тему Лист Мебиуса  Тема_5_2022
Тема_5_2022