Содержание
- 3. Конъюнктивной нормальной формой (КНФ) называется произвольная конъюнкция дизъюнктивных одночленов. Дизъюнктивной нормальной формой (ДНФ) называется произвольная дизъюнкция
- 4. Всякую формулу равносильными преобразованиями можно привести к ДНФ и КНФ. Алгоритм: Избавиться от операций импликации, эквивалентности,
- 5. Замечание: Для того чтобы проверить правильно ли привели формулу к КНФ и ДНФ, можно построить таблицы
- 6. Одночлен от некоторых переменных называется совершенным, если каждая из этих переменных входит в него ровно один
- 7. Теорема 1: Если формула не тождественно истинная, то для нее существует и при том единственная СКНФ.
- 8. Алгоритм нахождения СДНФ: Строим таблицу истинности; Выбираем те строки таблицы, на которых формула принимает значение истина;
- 10. Скачать презентацию







 Обратная функция. Равносильность уравнений
Обратная функция. Равносильность уравнений Неравенства. Решение линейных неравенств
Неравенства. Решение линейных неравенств Свойства и графики тригонометрических функций
Свойства и графики тригонометрических функций Урок математики. Повторение изученного
Урок математики. Повторение изученного Чтение девятизначных чисел
Чтение девятизначных чисел Формулы приведения. Математический диктант
Формулы приведения. Математический диктант Техника расчёта квадратов целых чисел
Техника расчёта квадратов целых чисел Таблица сложения
Таблица сложения Повторение. Дроби
Повторение. Дроби Презентация на тему Прогрессии
Презентация на тему Прогрессии  Математический тренажер
Математический тренажер Сравнение чисел. Геометрические величины. Геометрические фигуры
Сравнение чисел. Геометрические величины. Геометрические фигуры Математика
Математика Сокращение дробей. Тождество
Сокращение дробей. Тождество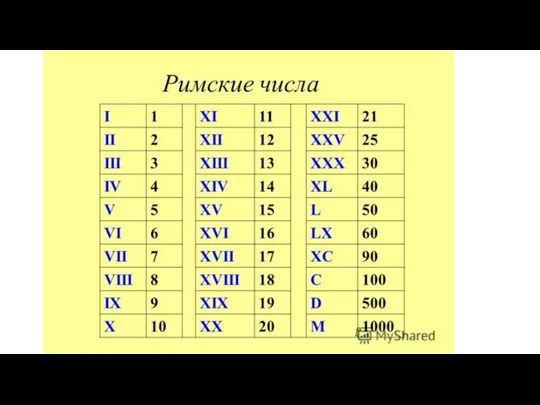 Римские числа
Римские числа Некоторые ошибки интерпретации относительных величин
Некоторые ошибки интерпретации относительных величин Задачи о дачном участке
Задачи о дачном участке Презентация на тему ПЕРЕМЕСТИТЕЛЬНОЕ СВОЙСТВО СЛОЖЕНИЯ
Презентация на тему ПЕРЕМЕСТИТЕЛЬНОЕ СВОЙСТВО СЛОЖЕНИЯ  Логические задачки на умение ориентироваться в числовом ряду
Логические задачки на умение ориентироваться в числовом ряду Параллельные прямые. Тест
Параллельные прямые. Тест Конус, его элементы и виды конусов
Конус, его элементы и виды конусов Задания по математике (5 класс, часть 7)
Задания по математике (5 класс, часть 7) Движение в пространстве
Движение в пространстве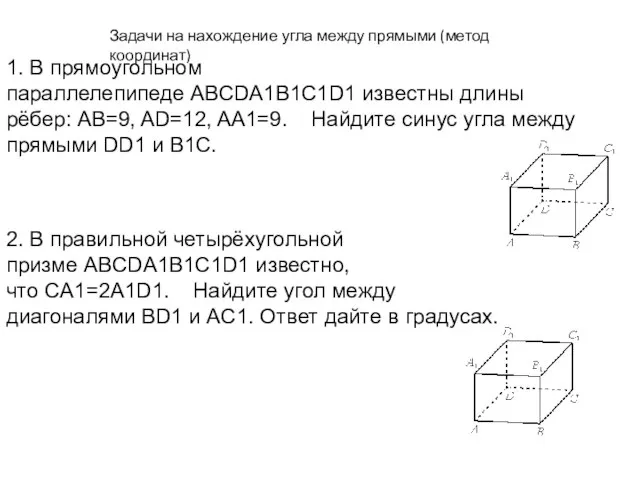 Задачи на нахождение угла между прямыми (метод координат)
Задачи на нахождение угла между прямыми (метод координат) Презентация на тему Объём шара и его частей
Презентация на тему Объём шара и его частей  Организация поисковой и рефлексивной деятельности учащихся при решении планиметрических задач. ГИА 2013. Задачи №23
Организация поисковой и рефлексивной деятельности учащихся при решении планиметрических задач. ГИА 2013. Задачи №23 Геометрические фигуры вокруг нас
Геометрические фигуры вокруг нас Введение в математический анализ
Введение в математический анализ