Содержание
- 2. Несколько слов о статистике Кратко о том как охарактеризовать и сравнить Ваши данные Почти инструкция В
- 3. Статистический анализ данных Включает несколько этапов. Один из наиболее важных для вас разделов это Описательная (дескриптивная)
- 4. Типы данных Имеют некоторое числовое значение количественные дискретные Принимают строго определенные, как правило, целочисленные значения непрерывные
- 5. Описательная (дескриптивная) статистика Важно учитывать тип данных и параметры распределения, характеризующиеся показателями асимметрии и гистограммой распределения
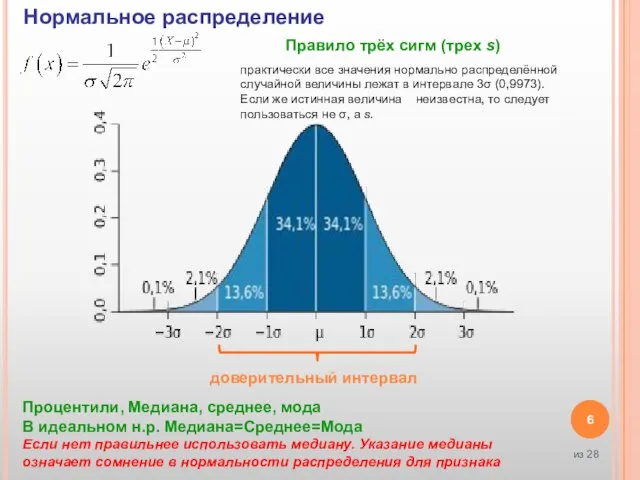
- 6. Нормальное распределение практически все значения нормально распределённой случайной величины лежат в интервале 3σ (0,9973). Если же
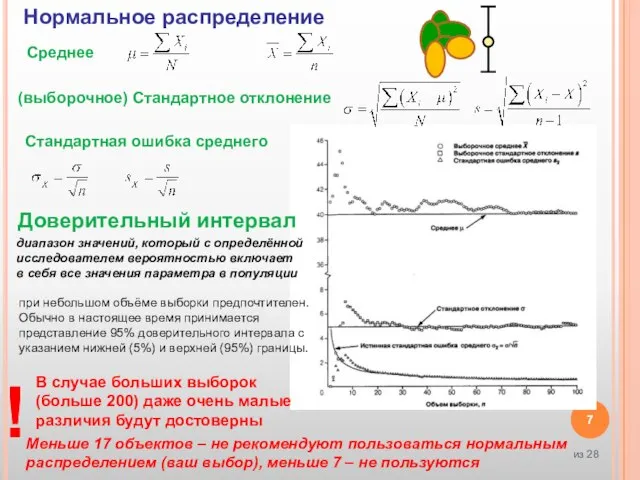
- 7. Среднее (выборочное) Стандартное отклонение Стандартная ошибка среднего ! В случае больших выборок (больше 200) даже очень
- 8. Параметрические методы анализируют нормально распределенные количественные признаки Непараметрические методы используются во всех остальных случаях (для анализа
- 9. - показатели разброса, описывающие степень разброса данных Описательная (дескриптивная) статистика Показатели описательной статистики показатели положения экспериментальных
- 10. Описательная (дескриптивная) статистика Показатели положения экспериментальных данных на числовой оси наиболее часто встречаемое значение в выборке.
- 11. Описательная (дескриптивная) статистика показатели разброса, описывающие степень разброса данных Стандартное отклонение Квантили характеризует собой частоту попадания
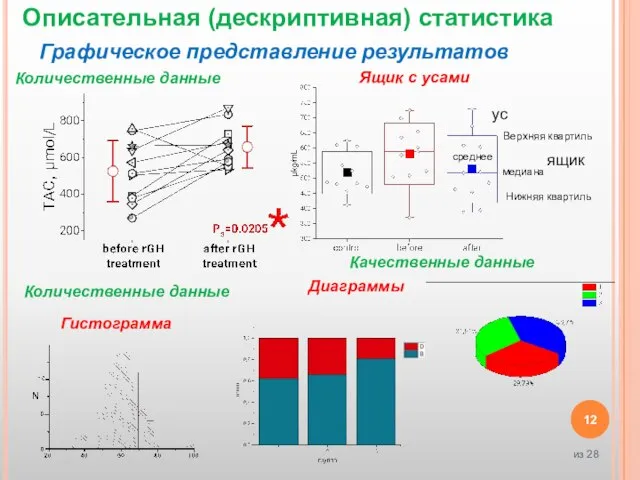
- 12. Описательная (дескриптивная) статистика Графическое представление результатов Гистограмма Количественные данные Количественные данные Качественные данные Диаграммы Ящик с
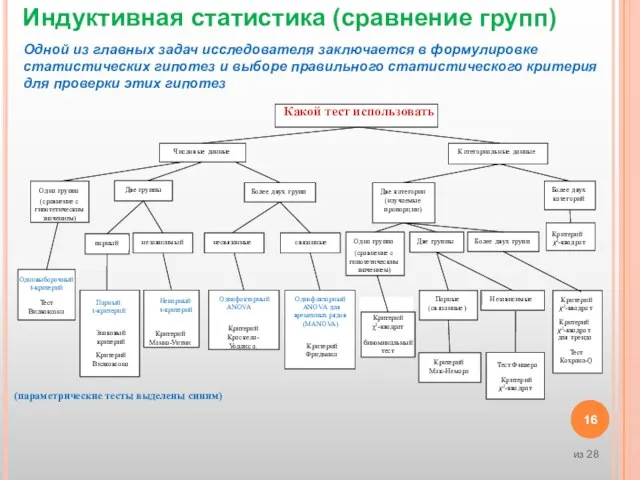
- 13. Индуктивная статистика Основная область применения – использование для сравнения двух (или более) выборок для определения их
- 14. Индуктивная статистика Типы ошибок Ошибка – обязательный компонент статистического анализа Допустимый уровень ошибок выбирается исследователем. Обычно
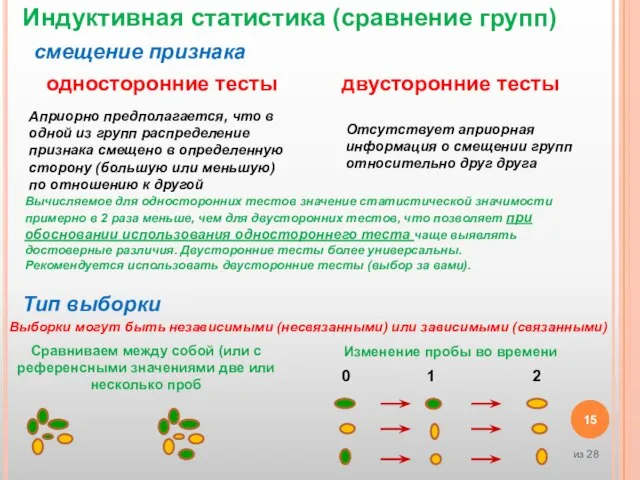
- 15. Индуктивная статистика (сравнение групп) смещение признака двусторонние тесты односторонние тесты Априорно предполагается, что в одной из
- 16. К а т ег ориа ль ные да нные Од на гру ппа Критерий Манна-Уитни Более
- 17. Статистическая обработка Как правильно обработать статистические данные? однозначного ответа нет, зависит от формы проведения эксперимента, количества
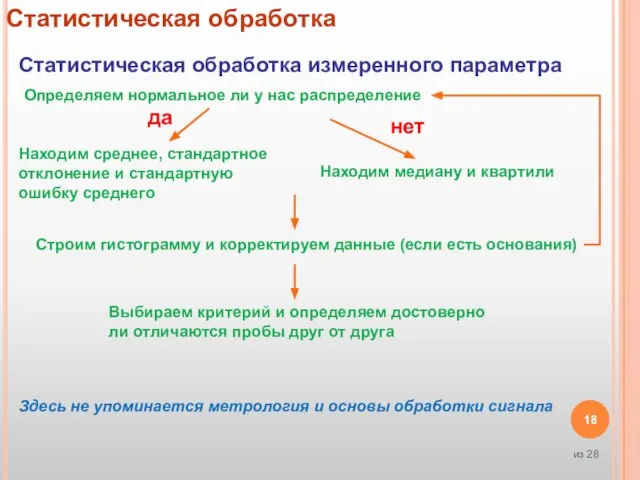
- 18. Статистическая обработка Статистическая обработка измеренного параметра Находим среднее, стандартное отклонение и стандартную ошибку среднего Строим гистограмму
- 19. Где и что про это можно прочитать Ищем методички для медиков, там мало объясняют, зато пишут
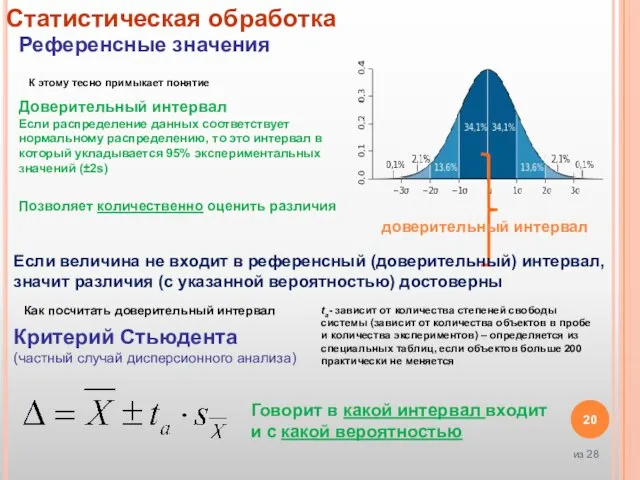
- 20. доверительный интервал Статистическая обработка Референсные значения Доверительный интервал Если распределение данных соответствует нормальному распределению, то это
- 21. Статистическая обработка Эффект множественных сравнений Вероятность ошибиться в одном из трех случаев Опасность попарного сравнения P=1-(1-α)k
- 22. Статистическая обработка оценка качественных переменных Оценивают не количество, а доли! Своя специфика в математике Стандартное отклонение
- 23. Программы для обработки изображений FIJI (ImageJ) Gwiddion Femtoskan SPIP Продукция компании Мекос Семейство программ Image Pro
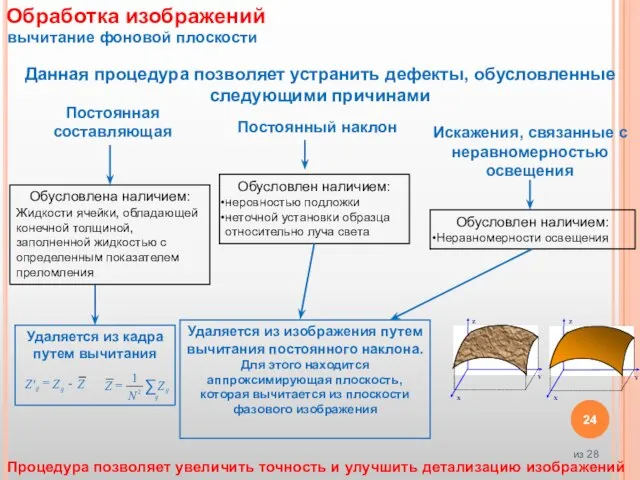
- 24. Данная процедура позволяет устранить дефекты, обусловленные следующими причинами Постоянная составляющая Постоянный наклон Искажения, связанные с неравномерностью
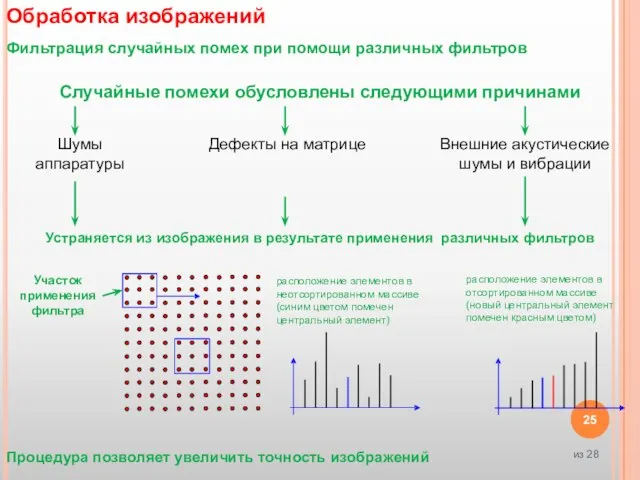
- 25. Обработка изображений Фильтрация случайных помех при помощи различных фильтров Случайные помехи обусловлены следующими причинами Процедура позволяет
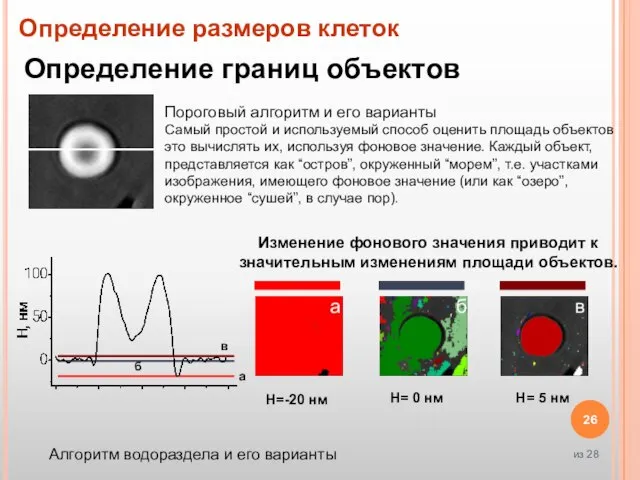
- 26. Определение размеров клеток Определение границ объектов Изменение фонового значения приводит к значительным изменениям площади объектов. Алгоритм
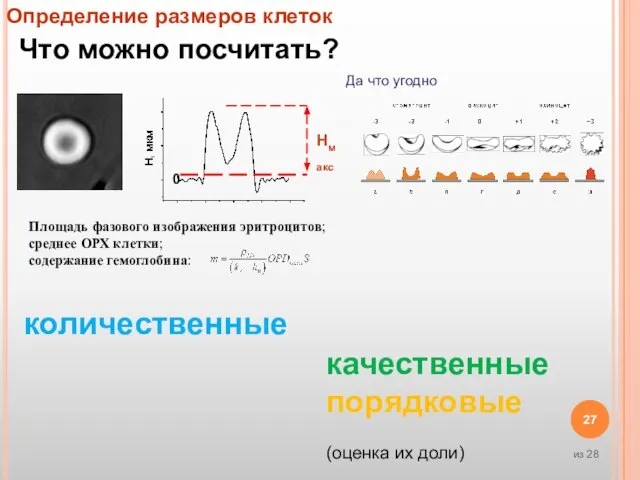
- 27. Определение размеров клеток Да что угодно Что можно посчитать? Площадь фазового изображения эритроцитов; среднее ОРХ клетки;
- 29. Скачать презентацию















 Ознакомление с задачей в 2 действия
Ознакомление с задачей в 2 действия Решение задач. Самостоятельная работа (ЕГЭ)
Решение задач. Самостоятельная работа (ЕГЭ) Аксиомы стереометрии. Взаимное расположение прямых и плоскостей в пространстве
Аксиомы стереометрии. Взаимное расположение прямых и плоскостей в пространстве Метод координат на плоскости
Метод координат на плоскости Иррациональные уравнения. Задания для устного счета
Иррациональные уравнения. Задания для устного счета Устные упражнения. Выразите в процентах
Устные упражнения. Выразите в процентах Стереометрия. Метод координат в задачах ЕГЭ
Стереометрия. Метод координат в задачах ЕГЭ Задание 19. Профиль (1)
Задание 19. Профиль (1) Переменные величины и их свойства
Переменные величины и их свойства Линейная алгебра. (Матрицы, определители)
Линейная алгебра. (Матрицы, определители) Презентация на тему Формулы сокращенного умножения. Представление выражения в виде многочлена
Презентация на тему Формулы сокращенного умножения. Представление выражения в виде многочлена  Динамическое программирование
Динамическое программирование Задачи на нахождение неизвестного
Задачи на нахождение неизвестного Решаем задачу
Решаем задачу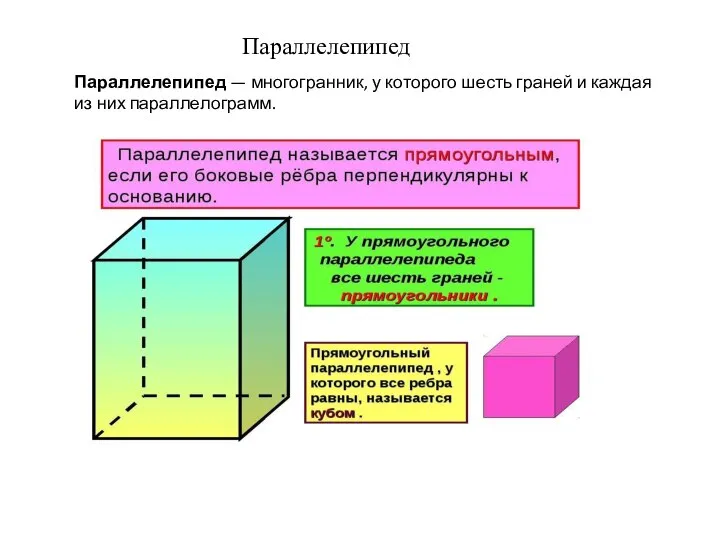 Параллелепипед
Параллелепипед Пирамида
Пирамида Решение задач с помощью систем уравнений (часть 2)
Решение задач с помощью систем уравнений (часть 2) Число и цифра 6. 1 класс
Число и цифра 6. 1 класс Задания 15 и 4
Задания 15 и 4 Прямой угол
Прямой угол Логарифмические уравнения и неравенства
Логарифмические уравнения и неравенства Функции, их свойства и графики
Функции, их свойства и графики Множественные связи. Порядковые и категоризованные переменные
Множественные связи. Порядковые и категоризованные переменные Уравнение сферы
Уравнение сферы Геометрический и физический смысл производной
Геометрический и физический смысл производной Площадь параллелограмма
Площадь параллелограмма Изображение фигур в пространстве
Изображение фигур в пространстве Решение тригонометрических уравнений и их систем
Решение тригонометрических уравнений и их систем