Симплекс-решетчатое планирование. Диаграммы состав-свойство Шеффе. Тема 8

Константой может быть единица или 100%, тонна, 1000 м3, т.е. надо знать, сколько и каких компонентов, в каком количестве необходимо для производства, например, одной тонны бумаги или 1000 м3 древесных плит.
Для решения таких задач используются симплекс-решетчатые планы (планы Шеффе). Им предложены простые планы эксперимента, позволяющие при малом количестве опытов получить для описания влияния соотношения компонентов на свойства продукции уравнения 1-го, 2-го и более высоких порядков. Экспериментальные точки располагаются в узлах сетчатой структуры в барицентрической системе координат.

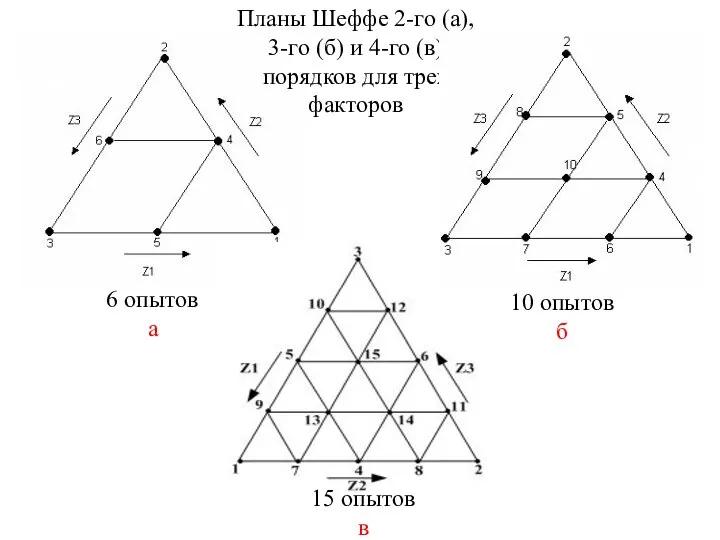
15 опытов
в
10 опытов
б
6 опытов
а
Планы Шеффе 2-го (а), 3-го (б) и 4-го (в) порядков для трех факторов

В вершинах симплекса смеси как таковой нет, т.к. там 100%-ное содержание одного из компонентов,
а экспериментальные точки на осях содержат не все компоненты. Следовательно, экспериментальные точки в вершинах глобального симплекса и на его осях не позволяют получить требуемую продукцию,
т.к. композиция (смесь) не содержит всех необходимых компонентов.
На практике рассматриваются, как правило, локальные симплексы, которые располагаются внутри глобальных и содержат все компоненты в том или ином количестве.

Формулы для расчета координат экспериментальных точек в единицах глобального симплекса:
для оси Z1:Z1 = Z1A + (Z1C – Z1A)X11 + (Z1B – Z1A)X21;
для оси Z2:Z2 = Z2C + (Z2B – Z2C)X21 + (Z2A – Z2C)X31;
для оси Z3:Z3 = 100 –Z1 – Z2
где Z1A, Z1B, Z1C, Z2A, Z2B, Z2C – координаты точек вершин локального симплекса по оси, %;
X11, X21, X31 – координаты экспериментальных точек локального симплекса.

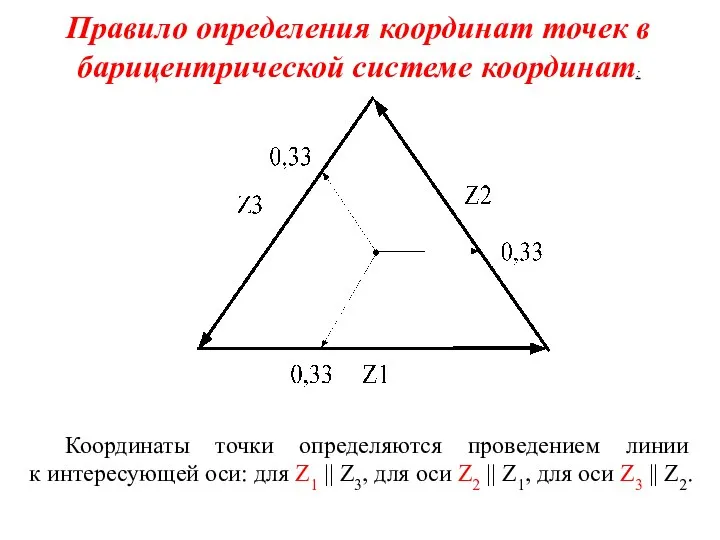
Правило определения координат точек в барицентрической системе координат:
Координаты точки определяются проведением линии к интересующей оси: для Z1 || Z3, для оси Z2 || Z1, для оси Z3 || Z2.

Расчет коэффициентов уравнения регрессии для локального симплекса производится по формулам:
b1 = y1;
b2 = y2;
b3 = y3;
b12 = 9/4(у4 + у5 – у1 – у2);
b13 = 9/4(у6 + у7 – у1 – у3);
b23 = 9/4(у8 + у9 – у2 – у3);
c12 = 9/4(3у4 – 3у5 – у1 + у2);
c13 = 9/4(3у6 – 3у7 – у1 + у3);
c23 = 9/4(3у8 – 3у9 – у2 + у3);
c123 = 27у10 – 27/4(у4 + у5 + у6 + у7 + у8 + у9) + 9/2(у1 + у2 + у3),
где у1–у10 – значения показателя в экспериментальных точках.

После расчета коэффициентов уравнения регрессии решается задача оптимизации с помощью электронных таблиц (см. лабораторную работу №6), где помимо ограничений, отражающих область определения факторов, вводится еще одно ограничение: сумма всех компонентов должна быть равна 1.