Окружность. Теоремы

Определение
ОКРУЖНОСТЬ —замкнутая плоская кривая, все точки которой одинаково удалены от ее центра O

Основные понятия
Радиус —отрезок, соединяющий центр окружности с одной из её точек.
Хорда-отрезок, соединяющий две точки окружности.
Диаметр- хорда проходящая через центр окружности,
Дуга окружности- любые две несовпадающие точки окружности делящие её на две части
Дуга называется полуокружностью, если отрезок, соединяющий её концы, является диаметром.
Дуга окружности- прямая, имеющая с окружностью ровно одну общую точку, а их общая точка называется точкой касания прямой и окружности.

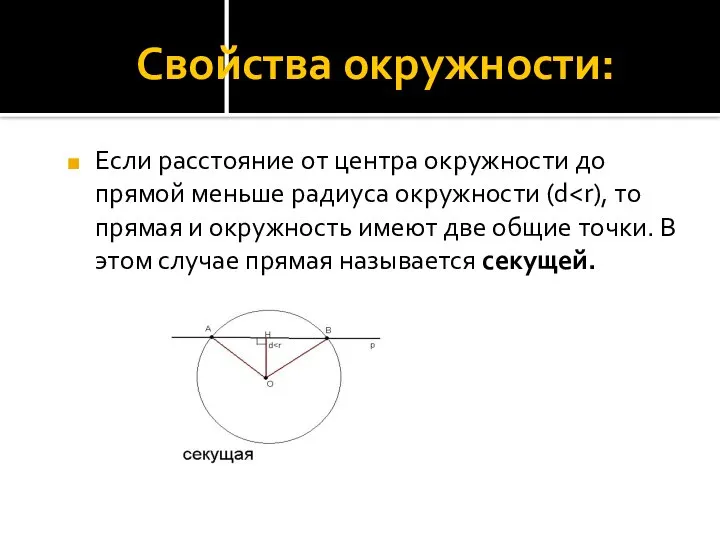
Свойства окружности:
Если расстояние от центра окружности до прямой меньше радиуса окружности (d то прямая и окружность имеют две общие точки. В этом случае прямая называется секущей.

Если расстояние от центра окружности до прямой равно радиусу окружности (d=r), то прямая и окружность имеют только одну общую точку

Если расстояние от центра окружности до прямой больше радиуса окружности(d>r), то прямая и окружность не имеют общих точек

Теорема 1
Теорема:
Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания.

Теорема 2
Если прямая проходит через конец радиуса, лежащий на окружности, и перпендикулярна к этому радиусу, то она является касательной.

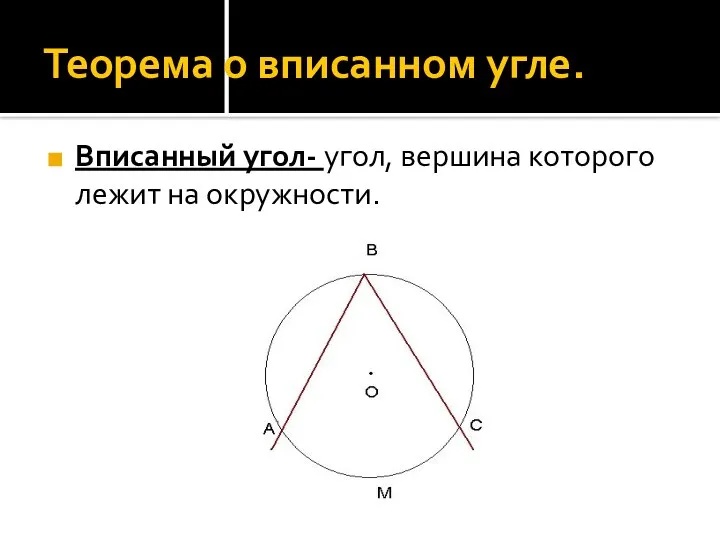
Теорема о вписанном угле.
Вписанный угол- угол, вершина которого лежит на окружности.

Теорема 3
Вписанный угол измеряется половиной дуги, на которую он опирается.

Луч ВО делит угол АВС на два угла. В этом случае луч ВО пересекает дугу АС в точке D. Точка D разделяет дугу АС на две дуги: AD и DC.
Из доказанного в п1:

СЛЕДСТВИЕ 1
Вписанные углы , опирающиеся на одну и ту же дугу , равны

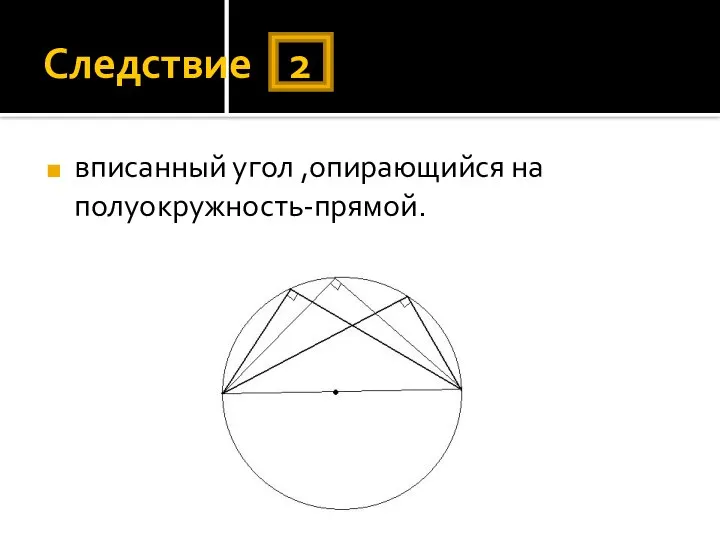
Следствие 2
вписанный угол ,опирающийся на полуокружность-прямой.

Теорема 4
Если две хорды окружности пересекаются , то произведение отрезков одной хорды равно произведению отрезков другой хорды.