Описанный четырехугольник

Признак
Четырехугольник можно описать около окружности если суммы противоположных сторон равны.
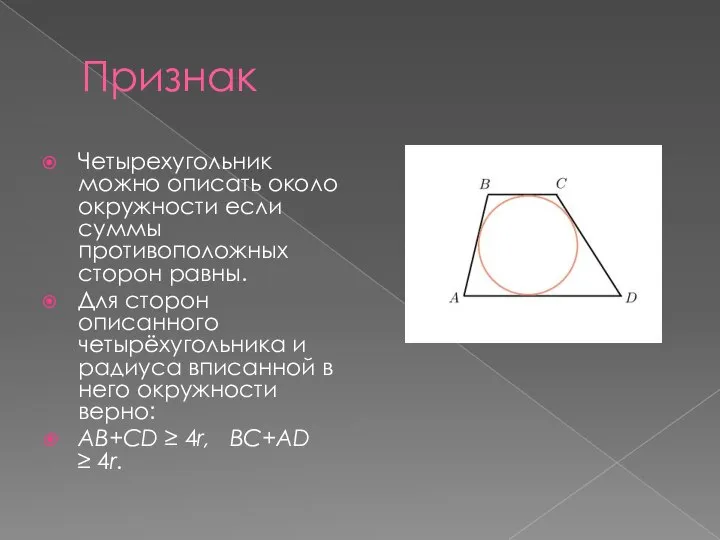
Для сторон описанного четырёхугольника и радиуса вписанной в него окружности верно:
AB+CD ≥ 4r, BC+AD ≥ 4r.

Свойства
Площадь описанного четырёхугольника:
S = pr,
где r – радиус вписанной окружности, p – полупериметр четырёхугольника.
Площадь описанного четырёхугольника:
S=√(AB*BC*CD*AD)*sin((AB+CD)/2)

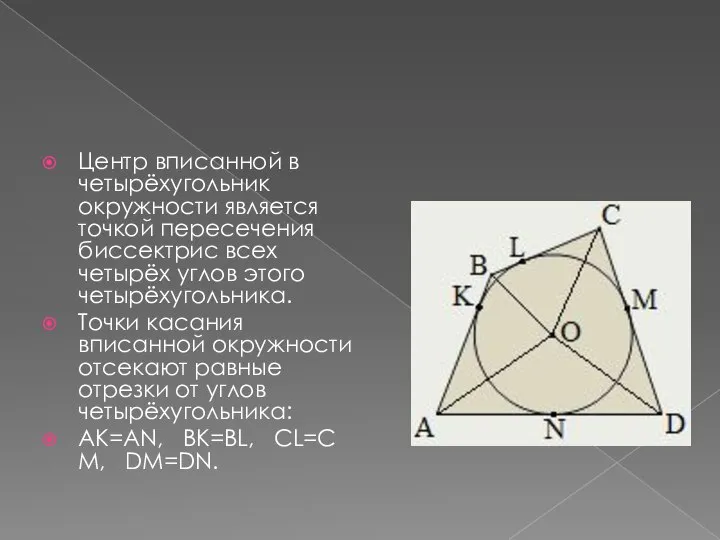
Центр вписанной в четырёхугольник окружности является точкой пересечения биссектрис всех четырёх углов этого четырёхугольника.
Точки касания вписанной окружности отсекают равные отрезки от углов четырёхугольника:
AK=AN, BK=BL, CL=CM, DM=DN.

Если O – центр окружности, вписанной в четырёхугольник ABCD, то
∠AOB+∠COD=∠BOC+∠AOD=180°.
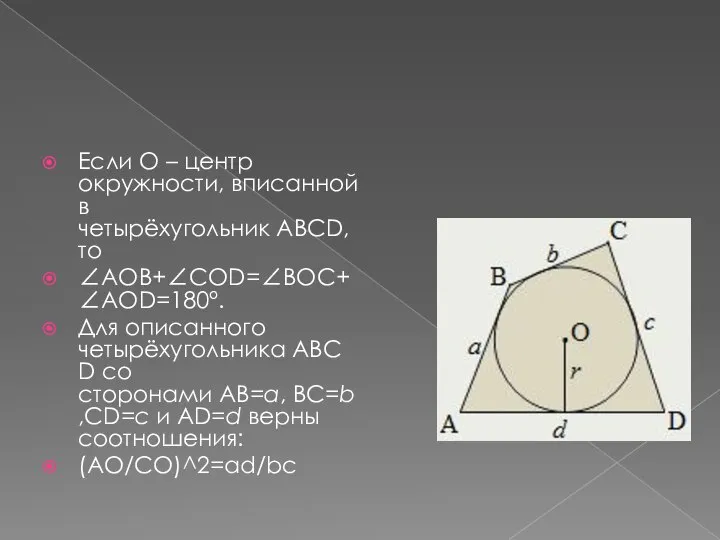
Для описанного четырёхугольника ABCD со сторонами AB=a, BC=b,CD=c и AD=d верны соотношения:
(AO/CO)^2=ad/bc