Определение координаты движущегося тела

Виды систем координат:
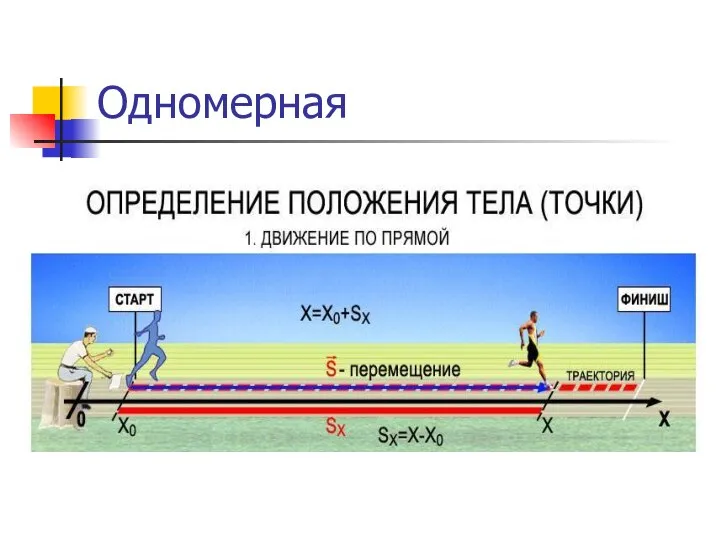
Одномерная
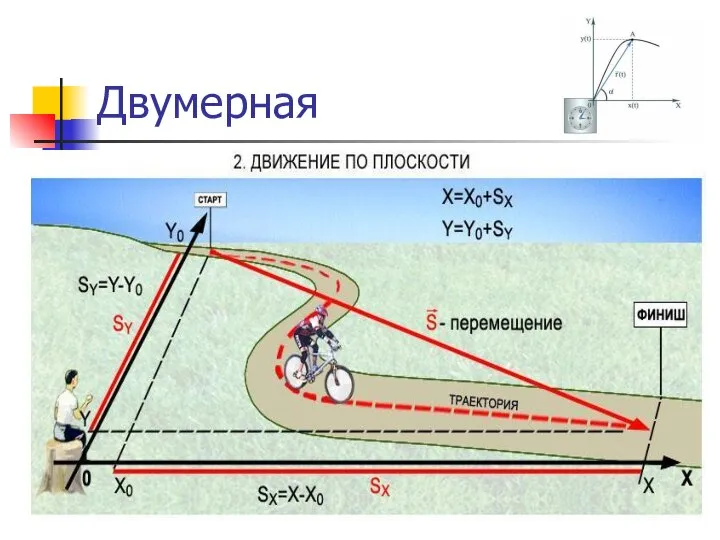
Двумерная
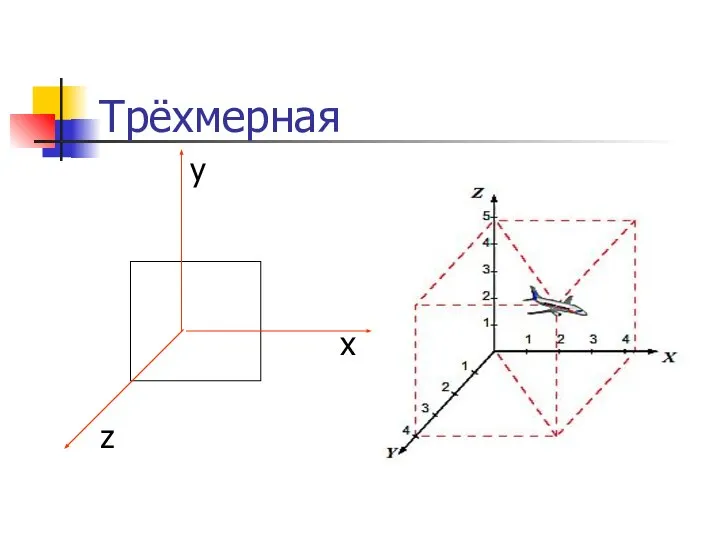
Трёхмерная
Для однозначного определения положения тела необходимо задать систему отсчета:
тело отсчета (тело, относительно которого рассматривается движение);
систему координат, связанную с телом отсчета;
часы, связанные с телом отсчета.

Одномерная

Двумерная

Трёхмерная
x
y
z

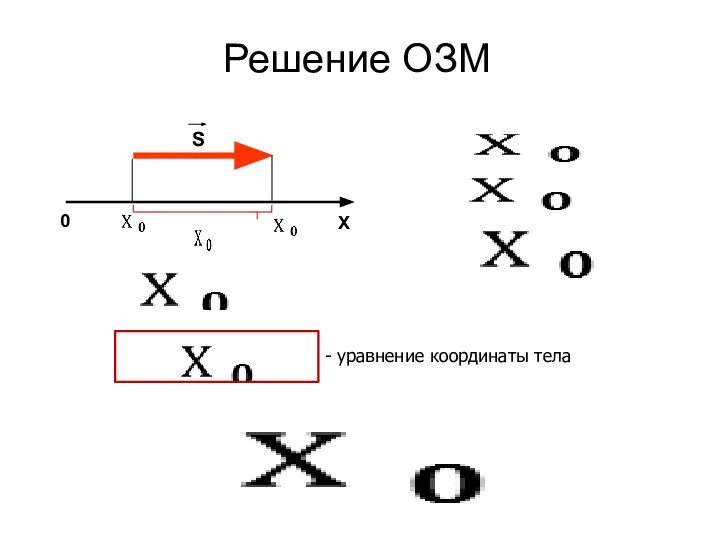
Решение ОЗМ
0
- уравнение координаты тела

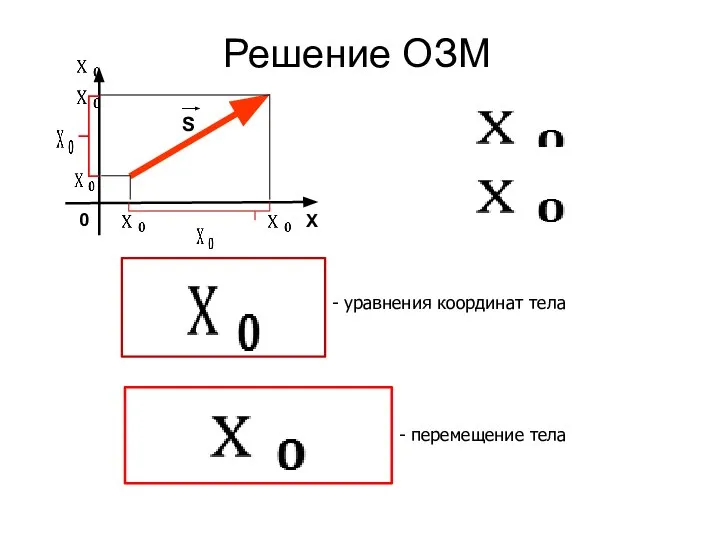
Решение ОЗМ
0
- уравнения координат тела
- перемещение тела

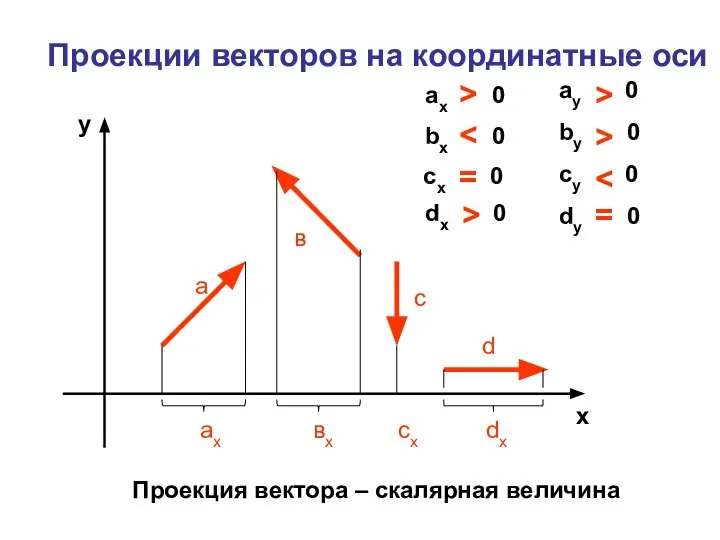
Проекции векторов на координатные оси

Проекции векторов на координатные оси
ax 0
bx 0
cx 0
dx 0
ay 0
by 0
cy 0
dy 0
>
<
=
>
>
>
<
=