Слайд 2Для успешной самореализации человека необходимо
Необходимость включения учеников в самостоятельную учебно-познавательную деятельность.
Овладение знаниями

,умениями и навыками происходит только в результате деятельности самого ребенка.
Самостоятельное добывание учащимися знаний обеспечивает более сознательное и глубокое усвоение учебного материала.
Более способные дети получают возможность полноценно развивать и реализовывать свои способности.
Слайд 6Типы самостоятельных работ
(в соответствии с уровнями самостоятельной деятельности )
Воспроизводящие.
Реконструктивно-вариативные
Эвристические
Творческие.

Слайд 7При проведении самостоятельной работы ставятся различные задачи
Отработка какого-то умения с целью довести

его до навыка. Проверка усвоения материала.
Проверка усвоения какого-то метода.
Проверка умения давать обоснования.
Контроль знаний.
В зависимости от цели самостоятельной работы допускается или не допускается помощь учителя, другого ученика, учебника. Оказывается помощь тем ученикам, которые не справляются с заданием.
Решение учеником домашних задач тоже является самостоятельной работой.
Выполнение различных практических заданий, связанных с построениями ,всегда является самостоятельной работой.
Слайд 8Работа с текстом
Самостоятельное прочтение и осмысление прочитанного.
Выделение главного.
Формирование умения воспринимать

и воспроизводить информацию по контролирующим вопросам учителя.
Обучение умению самостоятельно вычленять в прочитанном узловые моменты.
Обучение самостоятельному составлению плана воспроизведения прочитанного математического текста.
Воспроизведение текста по составленному плану.
Слайд 9Самостоятельная работа учащихся при изучении нового материала
Формировать у учащихся глубокие и прочные

знания. Научить школьников учиться, научить самостоятельно овладевать знаниями.
Сознательное овладение знаниями. Знания, которые ученик усвоил сам, значительно прочнее тех, которые он получил после объяснения учителя. Привитие навыка самостоятельности в работе вообще.
Возможность в дальнейшем самостоятельно ликвидировать пробелы в знаниях.
Расширять знания, творчески применять их.
Предлагать учащимся вопросы, ответа на которые в учебнике нет и поэтому требуются размышления учащихся.
Обязательная проверка понимания изученного.
Слайд 10Вооружение учащихся
методами доказательства
Широкий эксперимент, предшествующий теореме.
Математически правильная речь учителя. Логика его

рассуждений.
Догадка, гипотеза, подмеченная закономерность.
Самостоятельная формулировка и доказательство теоремы.
Четкое выделение условия и заключения теоремы.
Слайд 11Введение понятия «пропорция»
Изучаемое понятие?
Из скольких слов состоит термин, обозначающий это понятие?

К какому более широкому понятию оно относится? Ключевое слово в определении пропорции. Какие понятия также определялись как равенство?
Составим родословную понятия пропорция.
Приведите примеры равенств, являющихся пропорцией, не являющихся пропорцией.
Проведите классификацию равенств. Установите связь между классами. Может ли пропорция быть уравнением? Тождеством? Может ли уравнение быть пропорцией ,тождеством?
Слайд 14Решение задач
Упражнения, которые помогают овладеть способами получения информации, неявно содержащейся в задаче.

Выводить следствия из непосредственно заданной информации.
Переосмысливать некоторые объекты в плане других понятий.
Заменить термин его определением.
Переходить от понятия к его характеристическим свойствам.
Использовать свойства понятия.
Интерпретировать символические записи.
Переводить содержание задачи на язык определенной теории .
Слайд 15Результаты
Учащиеся:
понимают и принимают цели математического образования,
ценят вклад математики в общее развитие человека,
умеют

оптимизировать свои действия,
умеют вырабатывать и принимать решения,
умеют проверять действия, исправлять ошибки,
умеют различать аргументированные и бездоказательные утверждения
имеют сформированные универсальные умения и навыки, являющиеся основой существования человека в социуме, что отвечает теме экспериментальной работы школы по адаптации учащихся.
Слайд 16Работу строила
на уроках и во внеклассной работе по предмету, создавая условия для

самостоятельной деятельности учащихся,
организация УД по усвоению понятия, правила, теоремы, методов решения задач через отбор учебного материала, оптимальный выбор методов и форм УД, например, нестандартная форма вопроса, задача - исследование, организация «открытия» знаний учащимися в процессе практической деятельности,
на занятиях спецкурса «Решение нестандартных задач» (школьный компонент образования, составительская программа).
во внеклассной работе (проект «Край родной, навек любимый» как классный руководитель 5- 9а ,10-11 б).
Слайд 17Реализация учебной программы осуществлялась через:
отбор содержания (комплексные задачи, проведение исследований с использованием

основных мыслительных операций, приложение математических знаний в других областях, система вопросов - ориентиров познавательного процесса и др.),
оптимальный выбор методов и форм работы (конструктор урока).
Слайд 18Технологический компонент
опыта (опора):
на способы оптимизации учебно-воспитательного процесса Ю.К.Бабанского,
теорию взаимосвязи обучения и

развития Л.В.Занкова,
технологию укрупнения дидактических единиц Эрдниева (на этапе изучения нового материала),
ТРИЗ Г.С. Альтшулера (на этапе закрепления материала),
эвристические программы решения нестандартных задач Л.М. Фридмана (на этапе обобщения материала),
метод проектов (на этапе систематизации и контроля знаний).


















 32046
32046 Признак параллельности прямых. Задачи для устной работы
Признак параллельности прямых. Задачи для устной работы Показатели вариации
Показатели вариации Прибавление числа 6 с переходом через десяток
Прибавление числа 6 с переходом через десяток Геометрические тела. Многогранники
Геометрические тела. Многогранники Перпендикулярность прямых и плоскостей
Перпендикулярность прямых и плоскостей Понятие производной
Понятие производной Tema1_TeoriaMnozhestv
Tema1_TeoriaMnozhestv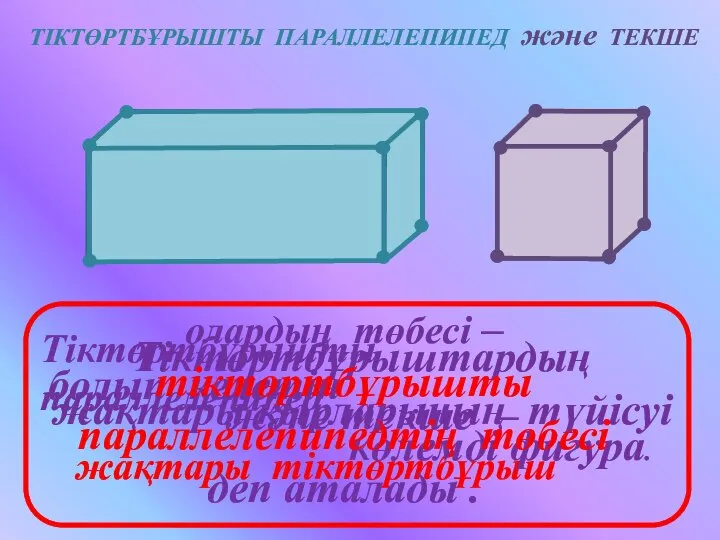 Тіктөртбұрышты параллелепипед және текше
Тіктөртбұрышты параллелепипед және текше Свойства логарифмов
Свойства логарифмов Элементы геометрии на небесной сфере. Лекция 1
Элементы геометрии на небесной сфере. Лекция 1 Признаки параллелограмма
Признаки параллелограмма Найдите все значения параметра a,
Найдите все значения параметра a, аксиомы стереометрии
аксиомы стереометрии Практикум по решению задач практической направленности
Практикум по решению задач практической направленности Умножение дробей
Умножение дробей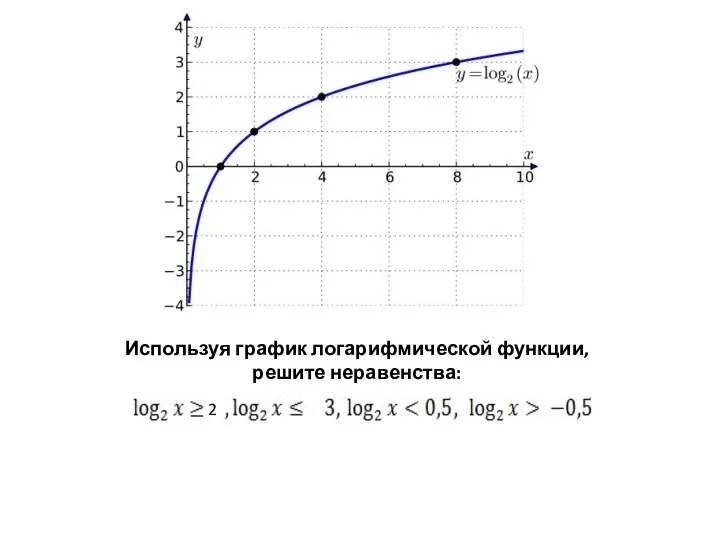 Логарифмические неравенства. устные упражнения
Логарифмические неравенства. устные упражнения Логарифмы. Логарифм числа. Основное логарифмическое тождество. Основные свойства логарифма
Логарифмы. Логарифм числа. Основное логарифмическое тождество. Основные свойства логарифма угол между прямой и плоскостью (1)
угол между прямой и плоскостью (1) Учимся писать цифры
Учимся писать цифры Векторы. Нулевой вектор
Векторы. Нулевой вектор Сравнение дробей. 1 часть
Сравнение дробей. 1 часть Живая планета!
Живая планета! Преобразование иррациональных выражений
Преобразование иррациональных выражений Арифметичская прогрессия
Арифметичская прогрессия Приём вычислений вида 35 - 7. 2 класс
Приём вычислений вида 35 - 7. 2 класс Волшебная страна математики: основы математики для детей 5-6 лет
Волшебная страна математики: основы математики для детей 5-6 лет Косинус острого угла прямоугольного треугольника
Косинус острого угла прямоугольного треугольника