Содержание
- 2. Определитель (или детерминант) – это число, связанное с квадратной матрицей А, обозначение: или det A. Если
- 3. Определитель 2-го порядка: det A= Определитель 3-го порядка: , det A=
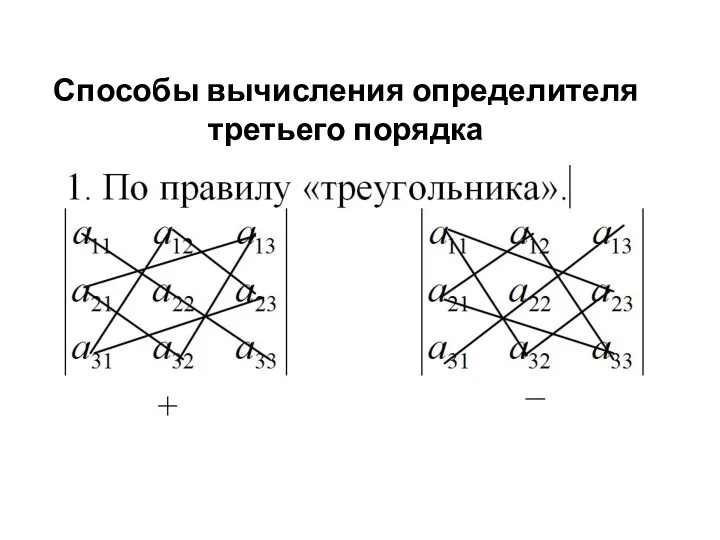
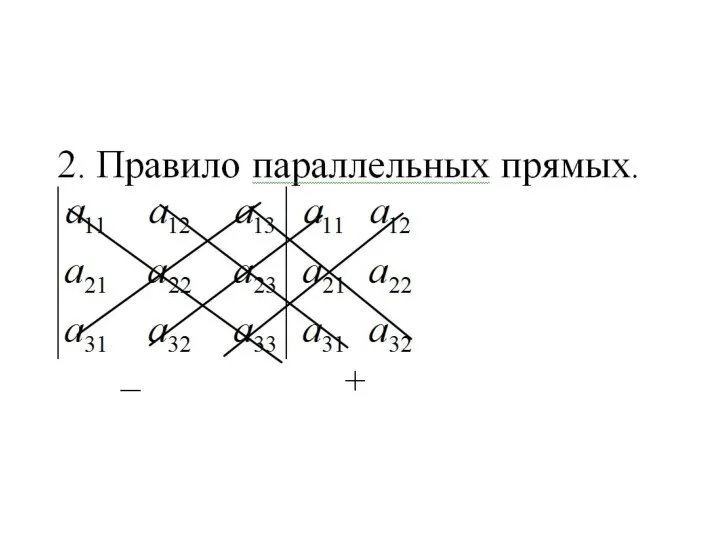
- 4. Способы вычисления определителя третьего порядка
- 6. Свойства определителей. При перемене местами любых двух строк (столбцов) определитель меняет знак на противоположный. При умножении
- 7. Если любую строку (столбец) определителя разбить в сумму двух строк (столбцов), то определитель можно представить как
- 8. Определитель, имеющий две одинаковые строки (столбца) равен нулю. Определитель, содержащий строку (строчку) из нулей, равен нулю.
- 9. Опр: Минор Мij элемента аij называется определитель, полученный из данного путем вычеркивания строки под номером i
- 10. Опр. Алгебраическое дополнение Аij - это минор Мij , умноженный на (-1)i+j, Аij = (-1)i+j Mij
- 11. Теорема Лапласа: Определитель равен сумме произведений элементов любой строки (столбца) на соответствующее алгебраическое дополнение этих элементов.
- 12. Обратная матрица
- 13. Рассмотрим квадратную матрицу n-го порядка А Опр. Квадратная матрица называется невырожденной, если ее определитель не равен
- 15. Скачать презентацию










 Повторение Обыкновенные дроби. Основное свойство дроби. Из частного (деления) Дробной чертой Числитель Знаменатель Сравни
Повторение Обыкновенные дроби. Основное свойство дроби. Из частного (деления) Дробной чертой Числитель Знаменатель Сравни Предметы геометрической формы. Логические задания
Предметы геометрической формы. Логические задания Системы уравнений и методы их решения
Системы уравнений и методы их решения Презентация на тему ГРАФИК ДВИЖЕНИЯ
Презентация на тему ГРАФИК ДВИЖЕНИЯ  Анализ уравнения на соответствие графику
Анализ уравнения на соответствие графику Числовые головоломки
Числовые головоломки Ряды Фурье
Ряды Фурье Сложение и вычитание дробей
Сложение и вычитание дробей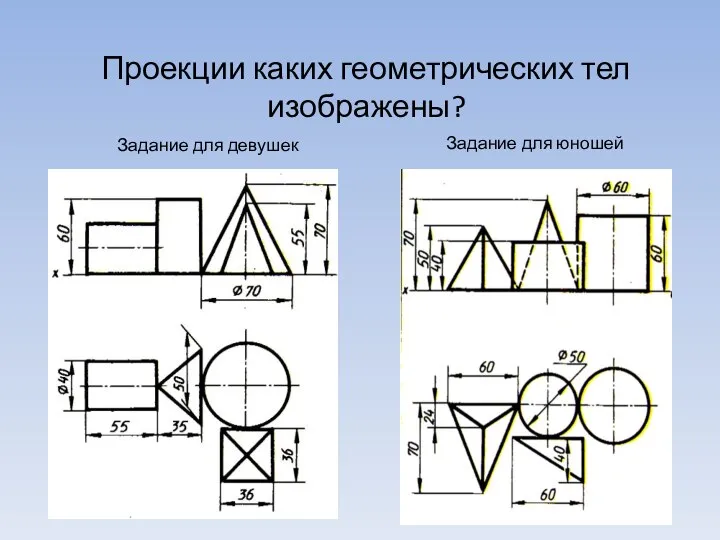 Проекции каких геометрических тел изображены?
Проекции каких геометрических тел изображены? День 3. Продающие тексты. Практика. Что продаем?
День 3. Продающие тексты. Практика. Что продаем? 8 класс
8 класс Площадь полной поверхности призмы
Площадь полной поверхности призмы Окружность и круг. Задачи
Окружность и круг. Задачи Презентация на тему Переменная
Презентация на тему Переменная  Прямые на плоскости
Прямые на плоскости Число π
Число π Квадратные неравенства
Квадратные неравенства Презентация на тему Теория вероятностей и комбинаторные правила
Презентация на тему Теория вероятностей и комбинаторные правила  Задачи ФИПИ
Задачи ФИПИ Презентация на тему Таблицы умножения и деления с числом 6
Презентация на тему Таблицы умножения и деления с числом 6  Математическая статистика
Математическая статистика Законы сложения и умножения
Законы сложения и умножения Элементы теории вероятности в практических задачах
Элементы теории вероятности в практических задачах Решение задач с параметрами
Решение задач с параметрами Презентация на тему Решение задач с помощью квадратных уравнений
Презентация на тему Решение задач с помощью квадратных уравнений  Преобразование графиков функции
Преобразование графиков функции Измерение объема жидких и сыпучих веществ с помощью условной меры масс
Измерение объема жидких и сыпучих веществ с помощью условной меры масс Теорема Виета. Урок систематизации, обобщения и контроля знаний
Теорема Виета. Урок систематизации, обобщения и контроля знаний