Содержание
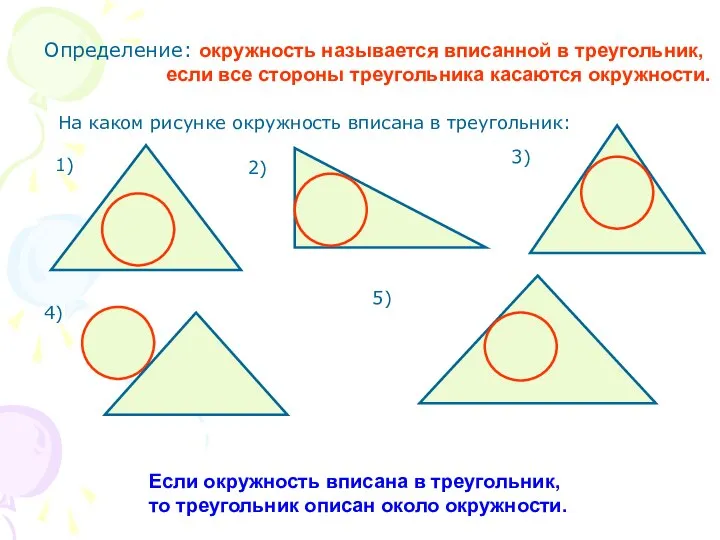
- 2. Определение: окружность называется вписанной в треугольник, если все стороны треугольника касаются окружности. Если окружность вписана в
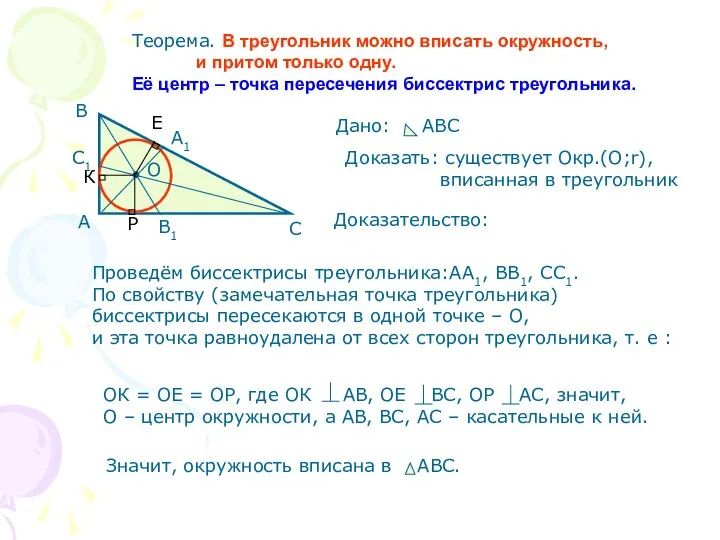
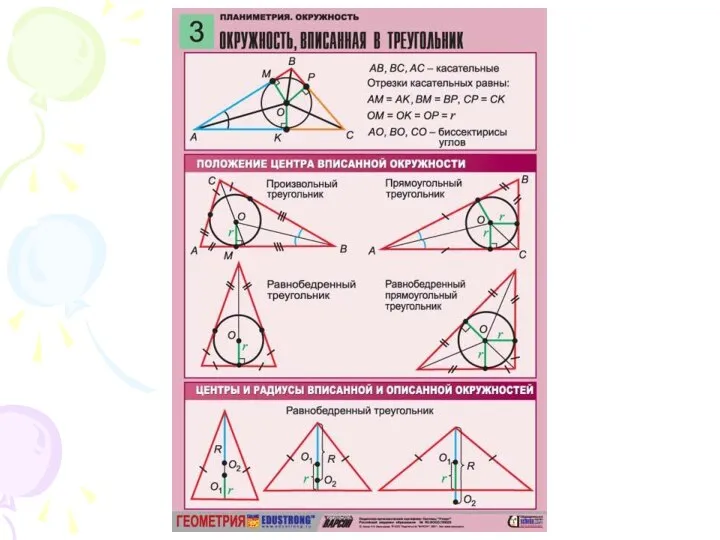
- 3. Теорема. В треугольник можно вписать окружность, и притом только одну. Её центр – точка пересечения биссектрис
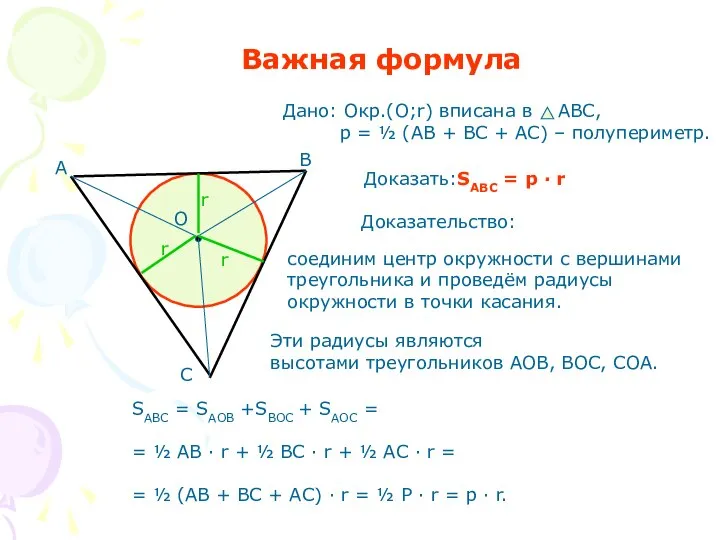
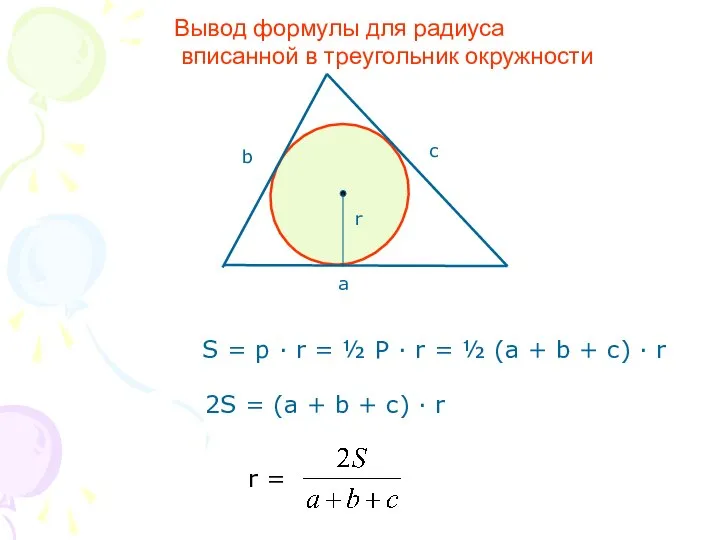
- 4. Важная формула Доказать:SABC = p · r Доказательство: Эти радиусы являются высотами треугольников АОВ, ВОС, СОА.
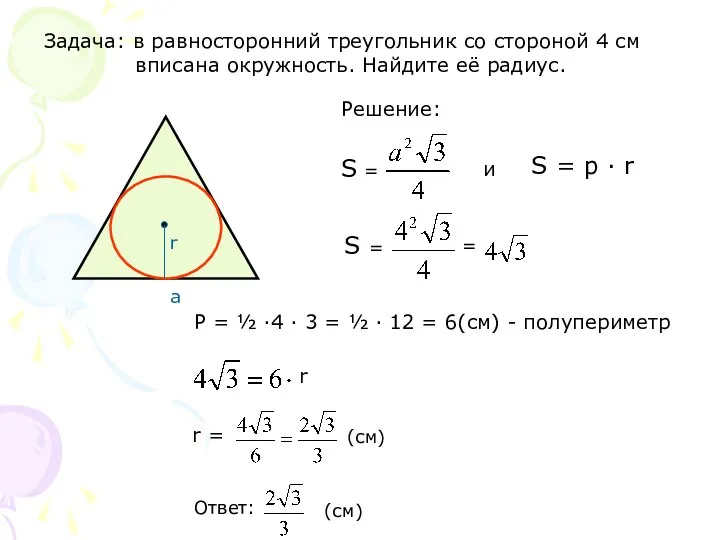
- 5. Задача: в равносторонний треугольник со стороной 4 см вписана окружность. Найдите её радиус. P = ½
- 6. S = p · r = ½ P · r = ½ (a + b +
- 7. Задача: в прямоугольный треугольник вписана окружность, гипотенуза точкой касания делится на отрезки 6 см и 4
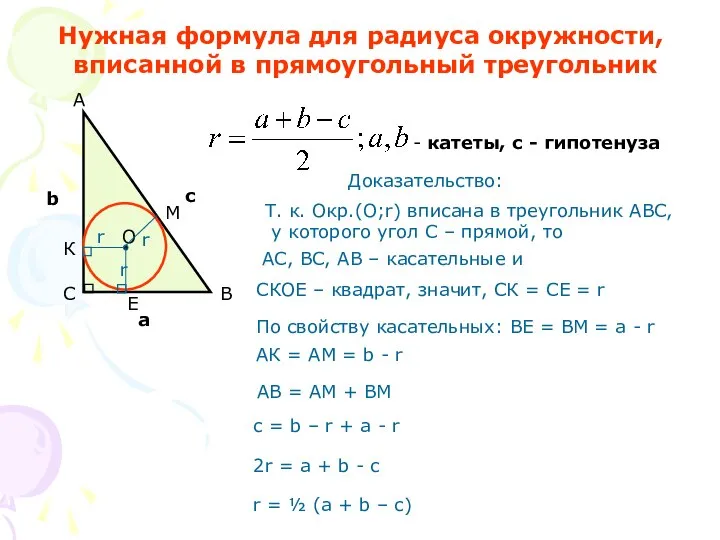
- 8. Нужная формула для радиуса окружности, вписанной в прямоугольный треугольник Доказательство: СКОЕ – квадрат, значит, СК =
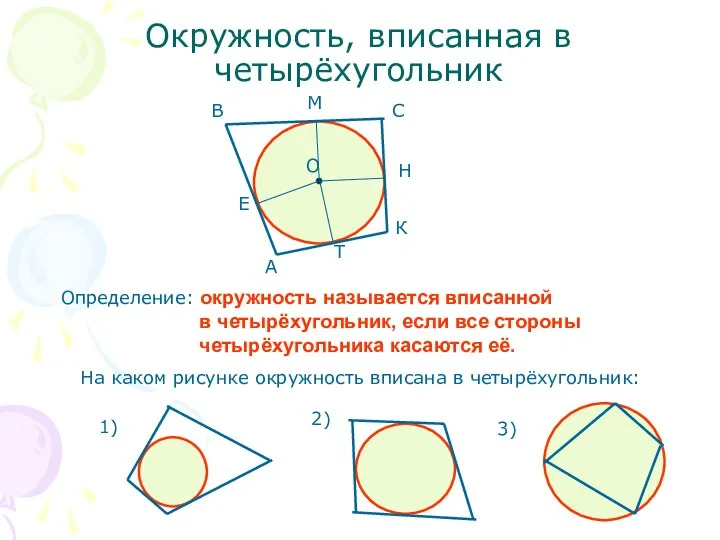
- 10. Окружность, вписанная в четырёхугольник Определение: окружность называется вписанной в четырёхугольник, если все стороны четырёхугольника касаются её.
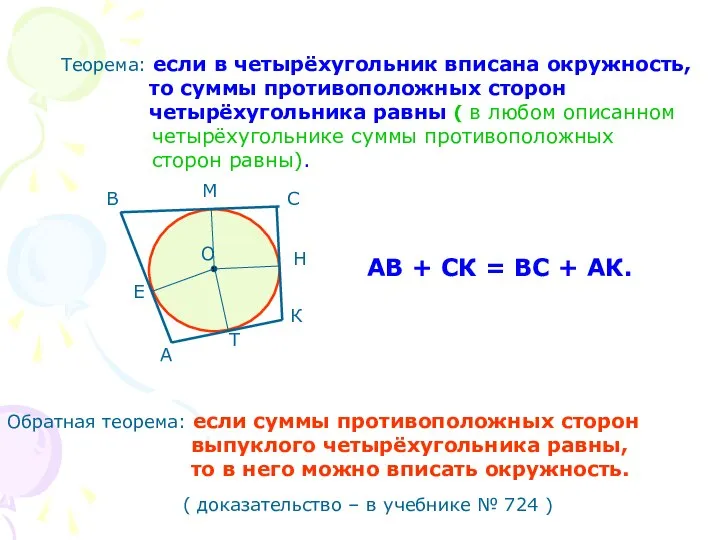
- 11. Теорема: если в четырёхугольник вписана окружность, то суммы противоположных сторон четырёхугольника равны ( в любом описанном
- 12. Задача: в ромб, острый угол которого 600, вписана окружность, радиус которой равен 2 см. Найти периметр
- 14. Скачать презентацию


 Задачи
Задачи 20140617_svoystva_funktsiy_9_klass
20140617_svoystva_funktsiy_9_klass Почти все об углах
Почти все об углах Презентация на тему Справочное пособие по геометрии
Презентация на тему Справочное пособие по геометрии  Введение таблицы умножения (Школа XXI века. Рудницкая В.Н )
Введение таблицы умножения (Школа XXI века. Рудницкая В.Н ) ложение комплексных чисел. Вычитание комплексных чисел
ложение комплексных чисел. Вычитание комплексных чисел Вычисление площадей
Вычисление площадей Ребуси Вавіліної Анастасії
Ребуси Вавіліної Анастасії Решение систем неравенств. 8 класс
Решение систем неравенств. 8 класс Виды кривых, замечательные кривые. Окружность и круг
Виды кривых, замечательные кривые. Окружность и круг Путешествие в страну дроби
Путешествие в страну дроби Решите неравенства
Решите неравенства Графики уравнений, содержащих модули
Графики уравнений, содержащих модули Сложение и вычитание смешанных чисел
Сложение и вычитание смешанных чисел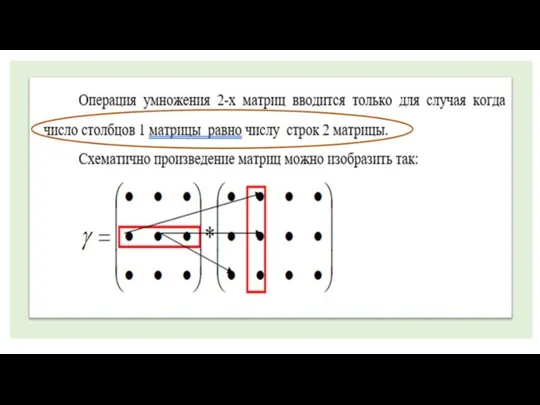 Операция умнодения 2 матриц
Операция умнодения 2 матриц Метод резолюций в алгебре высказываний
Метод резолюций в алгебре высказываний Все действия с дробями
Все действия с дробями Цифра ноль
Цифра ноль Осевая симметрия
Осевая симметрия Мода и медиана
Мода и медиана Этот вездесущий треугольник
Этот вездесущий треугольник Перехідна та імпульсна перехідна функції
Перехідна та імпульсна перехідна функції Тела вращения
Тела вращения Возведение комплексных чисел в степень
Возведение комплексных чисел в степень Векторы в пространстве. Решение задач по готовым чертежам
Векторы в пространстве. Решение задач по готовым чертежам Пифагор Самосский. Теорема Пифагора
Пифагор Самосский. Теорема Пифагора Приближенные числа. Округление чисел. Бородино 1812 г. 26 августа (7 сентября)
Приближенные числа. Округление чисел. Бородино 1812 г. 26 августа (7 сентября) Площадь круга. Геометрическая сказка. 6 класс
Площадь круга. Геометрическая сказка. 6 класс