Ориентация поверхности. Лист Мёбиуса

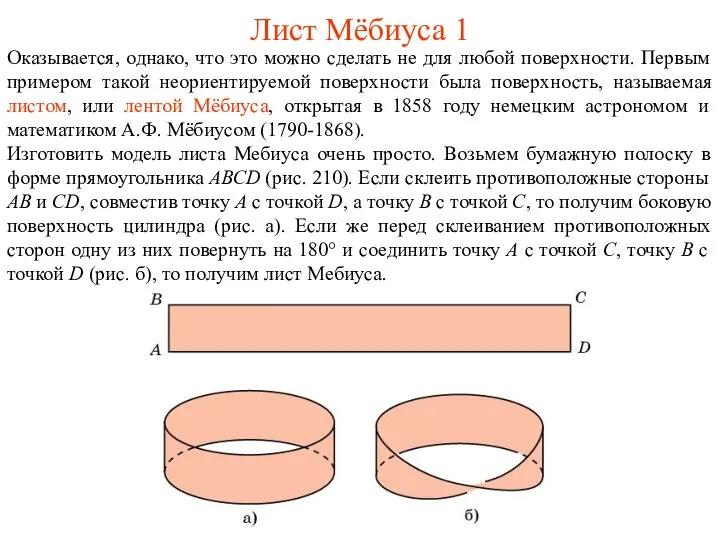
Лист Мёбиуса 1
Оказывается, однако, что это можно сделать не для любой поверхности. Первым примером такой неориентируемой поверхности была поверхность, называемая листом, или лентой Мёбиуса, открытая в 1858 году немецким астрономом и математиком А.Ф. Мёбиусом (1790-1868).
Изготовить модель листа Мебиуса очень просто. Возьмем бумажную полоску в форме прямоугольника АВСD (рис. 210). Если склеить противоположные стороны АВ и CD, совместив точку А с точкой D, а точку В с точкой С, то получим боковую поверхность цилиндра (рис. а). Если же перед склеиванием противоположных сторон одну из них повернуть на 180° и соединить точку A с точкой C, точку B с точкой D (рис. б), то получим лист Мебиуса.

Лист Мёбиуса 2
Лист Мёбиуса имеет только одну сторону. Муравью, ползущему по листу Мебиуса, не надо переползать через его край, чтобы попасть на противоположную сторону, как это видно на гравюре М. Эшера.
Свойство односторонности листа Мебиуса используется при изготовлении ременных передач. Если ремень сделать в виде ленты Мебиуса, то он будет изнашиваться вдвое медленнее, чем обычный. Это объясняется тем, что в работе ремня, изготовленного в виде ленты Мебиуса, принимает участие вся поверхность, а не только внутренняя ее часть, как у обычной ременной передачи.

Упражнение 1
Является ли ориентируемой: а) сфера; б) боковая поверхность цилиндра; в) поверхность конуса?
Ответ: а) Да;
б) да;
в) да.

Упражнение 2
Сколько сторон имеет тор (фигура в пространстве, форма которой напоминает баранку или бублик)?
Ответ: Две.

Упражнение 3
Является ли ориентируемой поверхностью: а) дважды перекрученная лента; б) трижды перекрученная лента?
Ответ: а) Да;
б) нет.

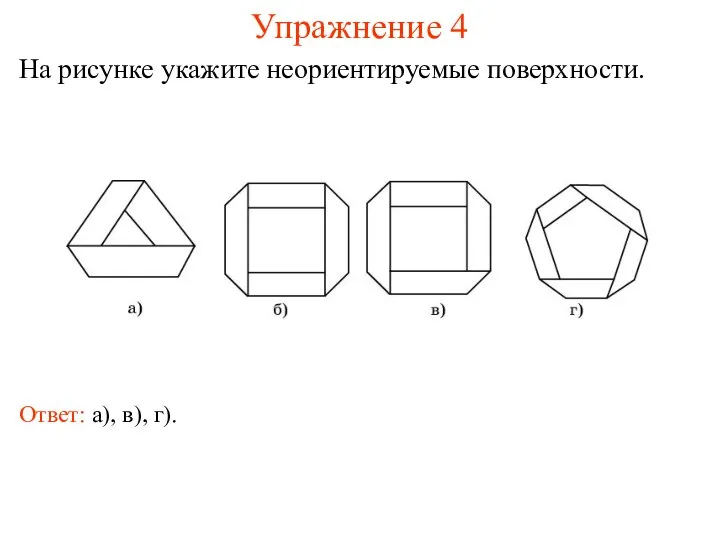
Упражнение 4
На рисунке укажите неориентируемые поверхности.
Ответ: а), в), г).

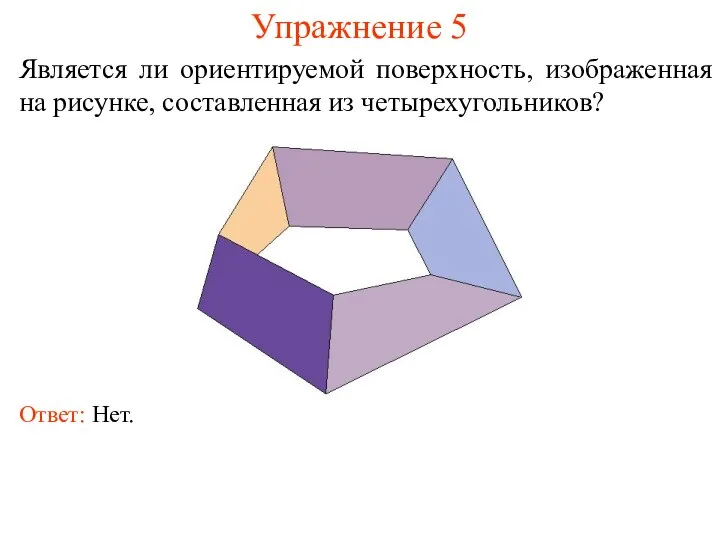
Упражнение 5
Является ли ориентируемой поверхность, изображенная на рисунке, составленная из четырехугольников?
Ответ: Нет.

Упражнение 6
Сколько сторон имеет поверхность, полученная при разрезании листа Мебиуса по средней линии?
Ответ: Две.

Упражнение 7
Что получится, если дважды перекрученную ленту разрезать по средней линии?
Ответ: Две сцепленные дважды перекрученные ленты.

Упражнение 8
Что получится, если лист Мебиуса разрезать не по средней линии, а отступив от края на треть ширины ленты?
Ответ: Сцепленные лист Мебиуса и четырежды перекрученная лента.

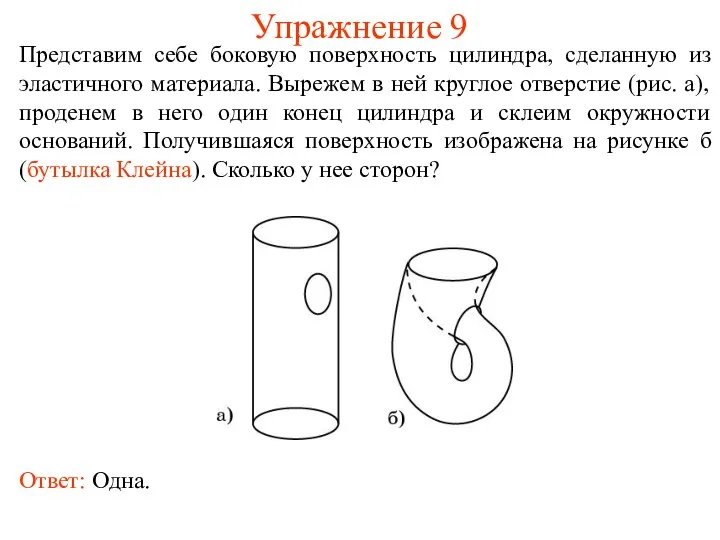
Упражнение 9
Представим себе боковую поверхность цилиндра, сделанную из эластичного материала. Вырежем в ней круглое отверстие (рис. а), проденем в него один конец цилиндра и склеим окружности оснований. Получившаяся поверхность изображена на рисунке б (бутылка Клейна). Сколько у нее сторон?
Ответ: Одна.

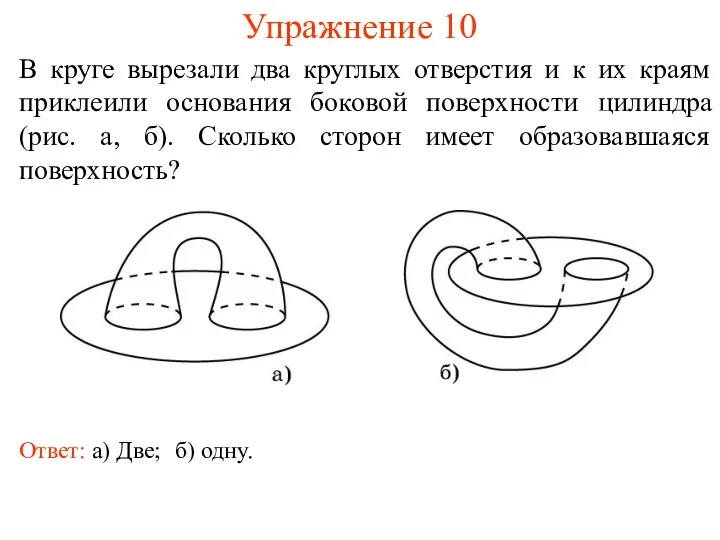
Упражнение 10
В круге вырезали два круглых отверстия и к их краям приклеили основания боковой поверхности цилиндра (рис. а, б). Сколько сторон имеет образовавшаяся поверхность?
Ответ: а) Две;
б) одну.