Слайд 2Актуальность
Каждый обучающийся стремится к сдаче ЕГЭ на максимальный балл и решение задач

сложного (творческого) уровня способствует достижению более высоких результатов, что актуально для каждого ученика, планирующего продолжить обучение после окончания 11 класса.
Слайд 3Цели программы
Устранить имеющиеся пробелы в знаниях;
Выработать навыки решения заданий повышенного уровня сложности

(профильного), входящих в Единый Государственный Экзамен;
Пробудить у обучающихся интерес к математике как науке.
Слайд 4Основные задачи программы
Показать обучающимся наиболее рациональные способы решения различных типов задач;
Показать обучающимся

различные вариации задач, встречающиеся в ЕГЭ;
Объяснить правила оформления решений задач повышенного уровня сложности;
Развить умение найти наиболее оптимальный метод решения конкретно поставленной задачи
Слайд 5Условия реализации программы
Данная программа рассчитана на обучающихся 11 класса
На 1 год обучения

(34 часа)
Занятия проводятся 1 раз в 2 недели по 2 академических часа (90 минут).
Слайд 6Содержание курса
Введение – 1 час
Решение задач по теме «Производная функции» – 3

часа
Решение текстовых задач на составление уравнений и систем уравнений – 6 часов
Решение геометрических задач (Планиметрия) – 5 часов
Решение задач по теме «Логарифмы» – 7 часов
Решение геометрических задач (Стереометрия) – 7 часов
Решение уравнений и неравенств – 5 часов
Итого: 34 часа
Слайд 7Формы организации деятельности на занятиях
Индивидуальная;
Групповая;
Фронтальная.

Слайд 8Формы организации контроля и оценки качества знаний
Тестирование;
Фронтальный опрос;
Дискуссия.

Слайд 9Обучающиеся должны знать
Основные понятия, связанные с темой «Производные»;
Методы составления уравнений для задач

с одной неизвестной и систем уравнений для задач с несколькими неизвестными;
Основные формулы планиметрии;
Основные понятия и формулы стереометрии;
Понятие логарифма и его свойства;
Графический способ решения задач с параметром.
Слайд 10Обучающиеся должны уметь
Выбрать рациональный метод решения поставленной задачи;
Преобразовывать выражения для упрощения дальнейшей

работы с ними;
Составлять уравнения и системы уравнений для решения текстовых задач;
Работать с графиками, диаграммами;
Выполнять геометрические построения различной степени сложности;
Строить математические доказательства









 Площадь многоугольника
Площадь многоугольника Теория вероятности. События и испытания
Теория вероятности. События и испытания Введение в геометрию
Введение в геометрию Правильные многоугольники
Правильные многоугольники Определение.Модуль числа а
Определение.Модуль числа а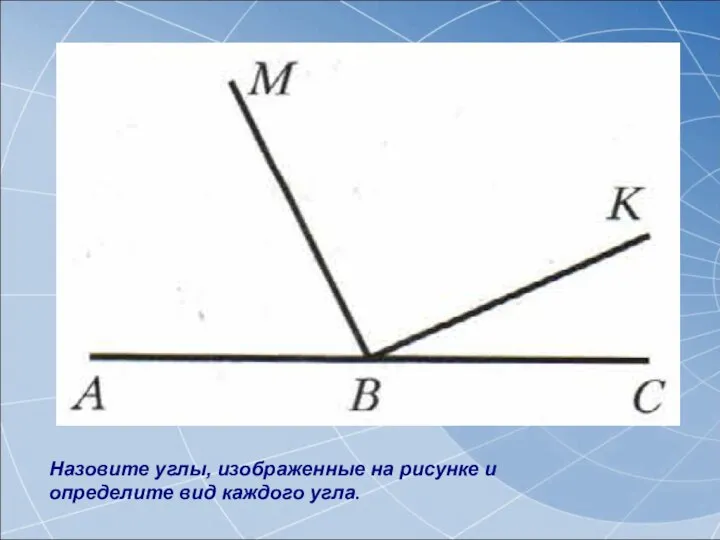 Виды треугольников. 5 класс
Виды треугольников. 5 класс Подобие фигур вокруг нас
Подобие фигур вокруг нас Презентация на тему Формулы сокращённого умножения
Презентация на тему Формулы сокращённого умножения  Задачи о дачном участке
Задачи о дачном участке Дроби и проценты. Арифметические действия с дробями
Дроби и проценты. Арифметические действия с дробями idkwhythatair
idkwhythatair Задачи на построение треугольника
Задачи на построение треугольника Презентация на тему Действия с десятичными дробями
Презентация на тему Действия с десятичными дробями  Модуль Начертательная геометрия. Тема 6
Модуль Начертательная геометрия. Тема 6 Осевая и центральная симметрии
Осевая и центральная симметрии О подобии произвольных фигур
О подобии произвольных фигур Математическая физминутка
Математическая физминутка Устный счёт. 3 класс
Устный счёт. 3 класс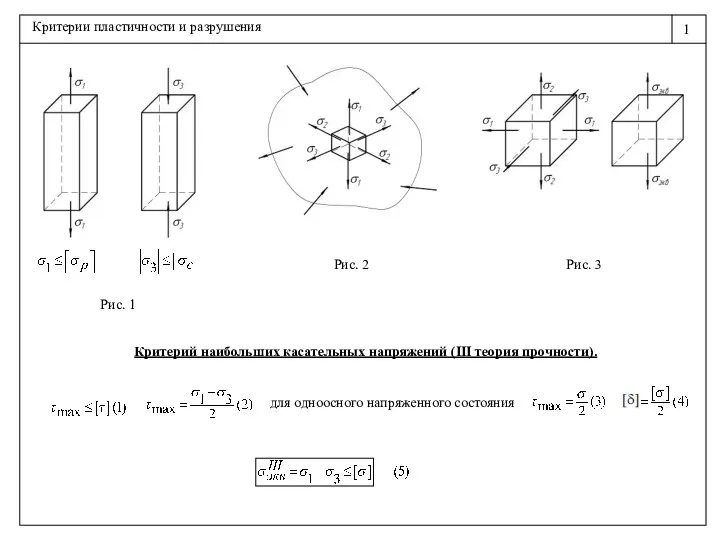 Критерии пластичности и разрушения
Критерии пластичности и разрушения Решение уравнений
Решение уравнений Множества иррациональных и действительных чисел
Множества иррациональных и действительных чисел Состав числа 9
Состав числа 9 Определение геометрической прогрессии. Формула n-го члена геометрической прогрессии
Определение геометрической прогрессии. Формула n-го члена геометрической прогрессии Презентация на тему Внетабличное умножение и деление. Приём деления для случаев вида 782, 693
Презентация на тему Внетабличное умножение и деление. Приём деления для случаев вида 782, 693 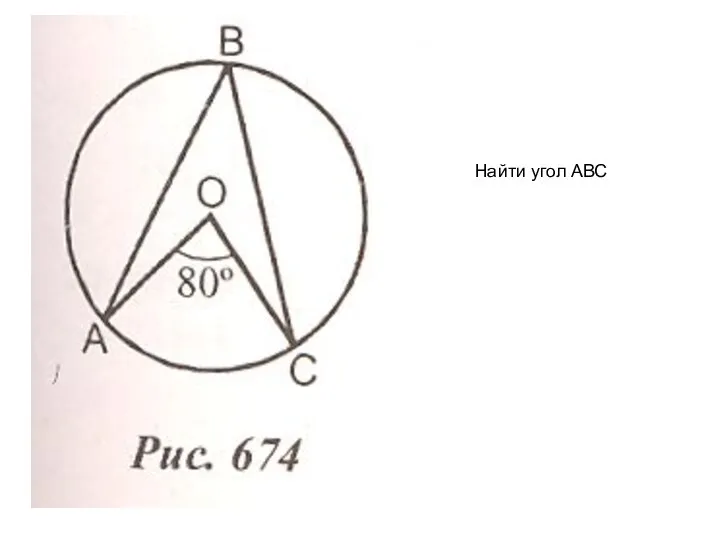 Найти угол АВС
Найти угол АВС Дискретный ряд распределения
Дискретный ряд распределения Преобразование логарифмических выражений
Преобразование логарифмических выражений Признаки подобия треугольников
Признаки подобия треугольников