Содержание
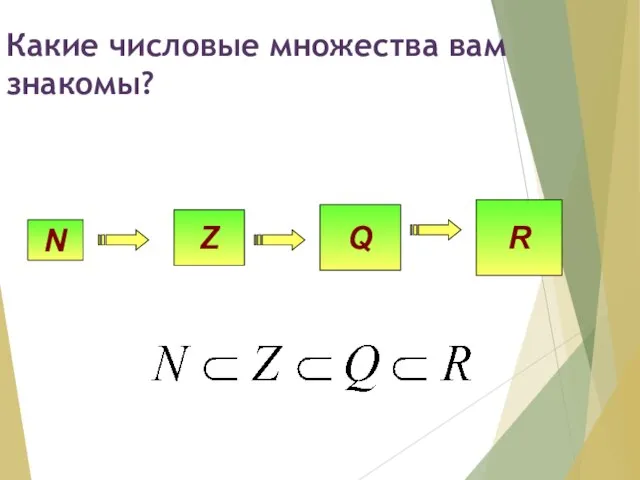
- 2. Какие числовые множества вам знакомы?
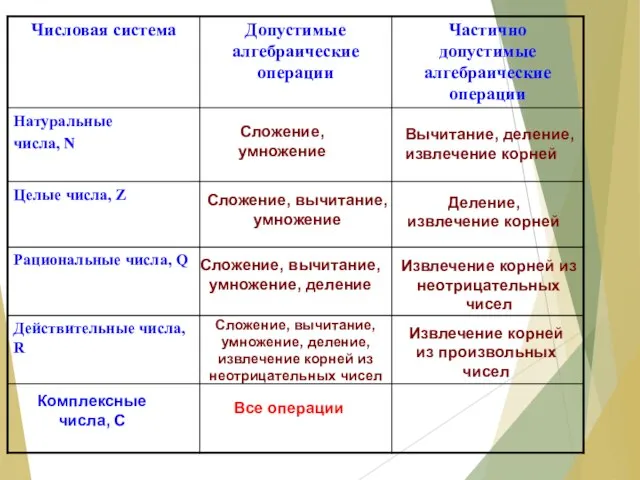
- 3. Сложение, умножение Вычитание, деление, извлечение корней Сложение, вычитание, умножение Деление, извлечение корней Сложение, вычитание, умножение, деление
- 4. Минимальные условия, которым должны удовлетворять комплексные числа: С1) Существует комплексное число, квадрат которого равен -1 .
- 5. Мнимые числа i, 2i, -0,3i — чисто мнимые числа Арифметические операции над чисто мнимыми числами выполняются
- 6. Определение 1. Комплексным числом называют сумму действительного числа и чисто мнимого числа. Определение 2. Два комплексных
- 7. Арифметические операции над комплексными числами (а + bi) + (c + di) = (а + с)
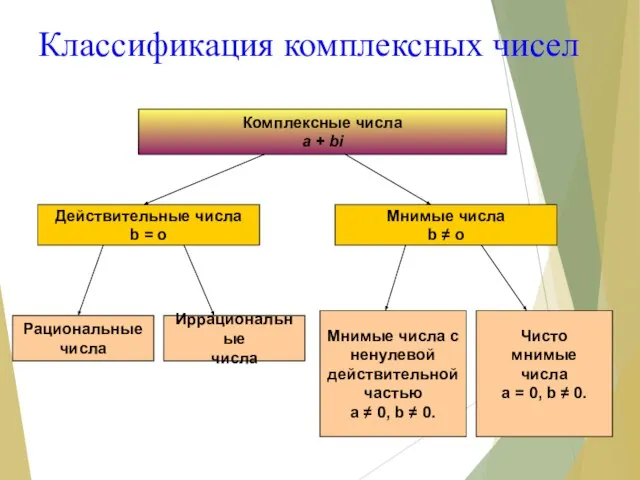
- 8. Классификация комплексных чисел Комплексные числа a + bi Действительные числа b = o Мнимые числа b
- 9. Сопряженные комплексные числа Определение: Если у комплексного числа сохранить действительную часть и поменять знак у мнимой
- 10. Свойства сопряженных чисел Сумма и произведение двух сопряженных чисел есть число действительное. Число, сопряженное сумме двух
- 11. Свойства сопряженных чисел Число, сопряженное п-ой степени комплексного числа z, равно п-ой степени числа, сопряженного к
- 12. Степени мнимой единицы По определению первой степенью числа i является само число i, а второй степенью
- 13. Извлечение квадратных корней из комплексных чисел в алгебраической форме. Определение. Число w называют квадратным корнем из
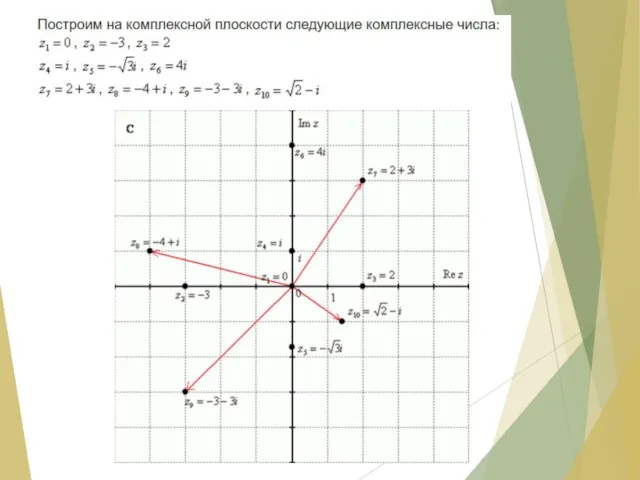
- 14. Геометрическое изображение комплексных чисел. Комплексному числу z на координатной плоскости соответствует точка М(a, b). Часто вместо
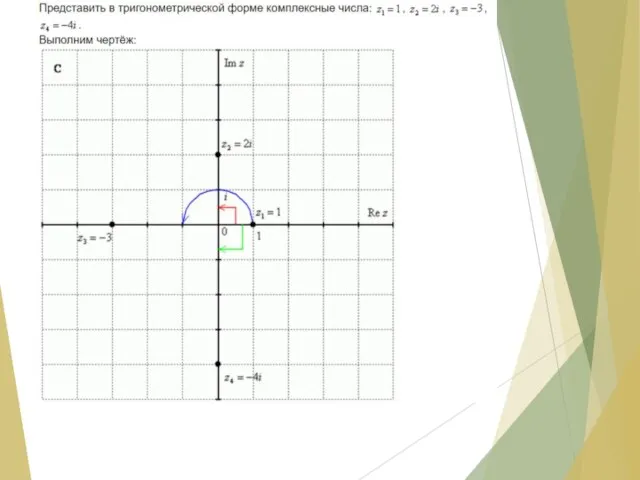
- 15. Тригонометрическая форма комплексного числа где φ – аргумент комплексного числа, r = - модуль комплексного числа,
- 16. Умножение и деление комплексных чисел, заданных в тригонометрической форме Теорема 1. Если и то: б) а)
- 17. Выполнить действия
- 22. Найти сумму, разность, произведение и частное комплексных чисел (3+17i)+(9+11i)= (6+8i) : (4+2i)= (2+6i)+(8+6i)= (16+3i) : (2+4i)=
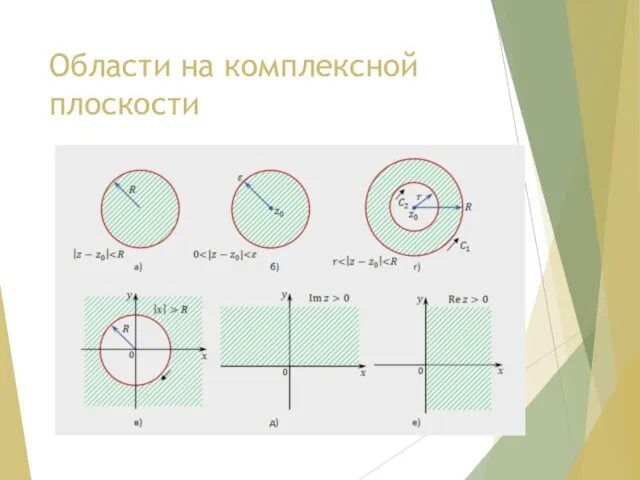
- 27. Области на комплексной плоскости
- 29. Скачать презентацию




















 Признаки параллелограмма
Признаки параллелограмма Олимпиадная математика
Олимпиадная математика Алгоритмически неразрешимые задачи и вычислимые функции
Алгоритмически неразрешимые задачи и вычислимые функции Площадь фигур. Единицы площади
Площадь фигур. Единицы площади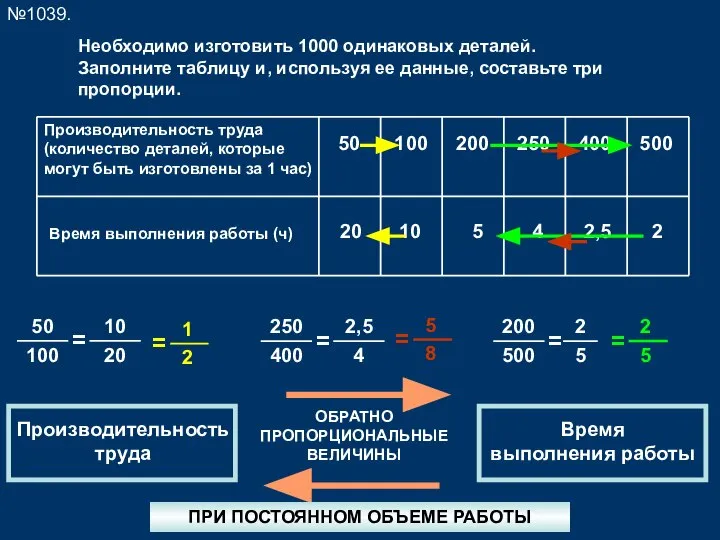 Пропорциональные величины
Пропорциональные величины Многочлены
Многочлены В мире рациональных уравнений
В мире рациональных уравнений Векторная алгебра
Векторная алгебра Знакомая незнакомка. Парабола
Знакомая незнакомка. Парабола Двугранный угол
Двугранный угол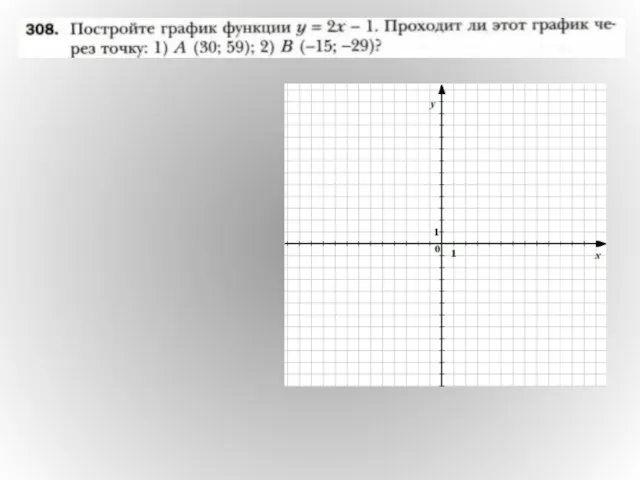 Функция y = k/х и её график
Функция y = k/х и её график Деление и дроби. Представление натуральных чисел дробями
Деление и дроби. Представление натуральных чисел дробями Конус - тело вращения
Конус - тело вращения Евклидовы пространства
Евклидовы пространства Система пропорционирования в проектировании объектов дизайна
Система пропорционирования в проектировании объектов дизайна Координатная плоскость. 6 класс
Координатная плоскость. 6 класс Xüsusi törəməli diferensial tənliklərin həlli metodları
Xüsusi törəməli diferensial tənliklərin həlli metodları Знакомство с линейкой, единицей измерения длины – сантиметр (2 урок)
Знакомство с линейкой, единицей измерения длины – сантиметр (2 урок) Среднее арифметическое чисел
Среднее арифметическое чисел Окружность. 7 класс
Окружность. 7 класс Презентация4. МСиТИ
Презентация4. МСиТИ Первый признак равенства треугольников
Первый признак равенства треугольников Отношения рядом стоящих чисел в пределах 10
Отношения рядом стоящих чисел в пределах 10 Физико-математические основы ОФЭКТ
Физико-математические основы ОФЭКТ Проценты. ОГЭ и ЕГЭ
Проценты. ОГЭ и ЕГЭ Применение распределительного свойства умножения
Применение распределительного свойства умножения Презентация на тему ГЕОМЕТРИЧЕСКИЕ ТЕЛА И ПЛОСКИЕ ФИГУРЫ
Презентация на тему ГЕОМЕТРИЧЕСКИЕ ТЕЛА И ПЛОСКИЕ ФИГУРЫ 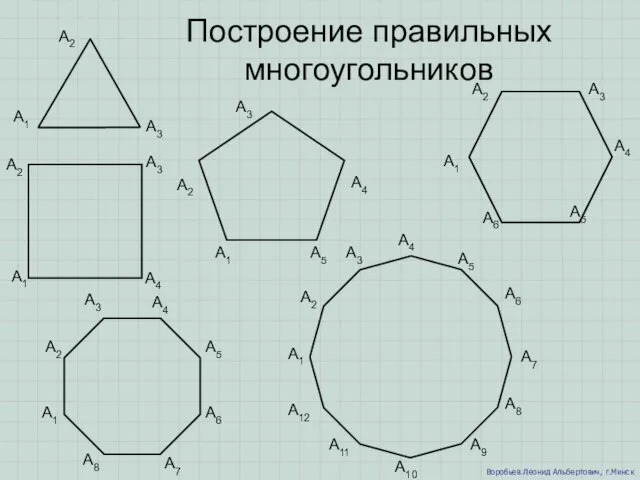 Презентация на тему Построение правильных многоугольников
Презентация на тему Построение правильных многоугольников