Содержание
- 2. Задача о счастливом билете
- 3. Задача о счастливом билете k=9
- 4. Длина половины номера
- 5. Числовые характеристики дискретной случайной величины Неслучайная (постоянная величина)
- 6. Формула для вычисления дисперсии const const
- 7. Свойства дисперсии
- 8. Дисперсия числа появлений событий в независимых испытаниях n независимых испытаний Событие A появляется в каждом из
- 9. Среднее квадратическое отклонение сигма Ответ. Данная случайная величина X имеет мат.ожидание 6,4, дисперсию 13,04 и среднее
- 10. От дискретности – к непрерывности!
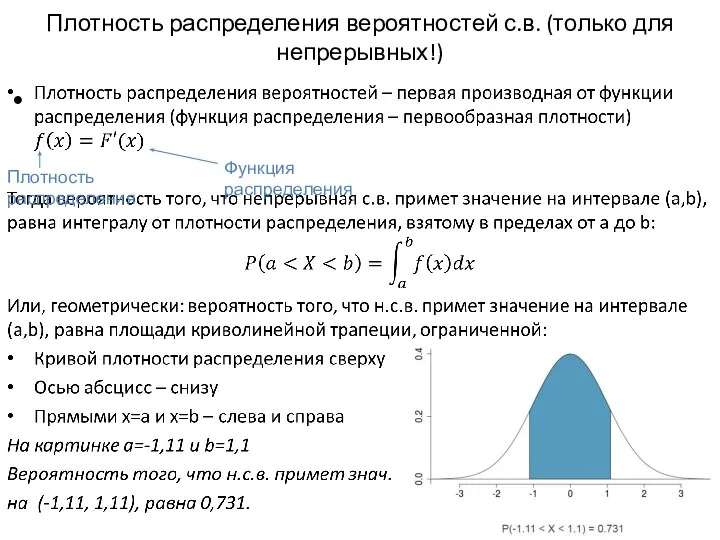
- 11. Плотность распределения вероятностей с.в. (только для непрерывных!) Плотность распределения Функция распределения
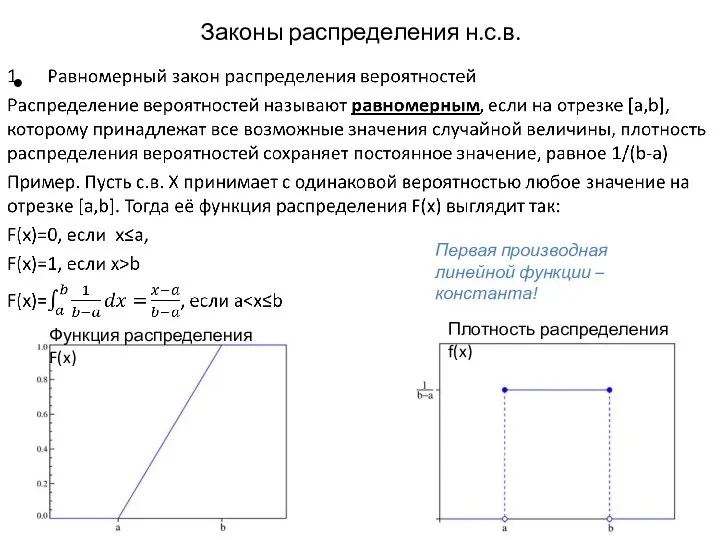
- 12. Законы распределения н.с.в. Функция распределения F(x) Плотность распределения f(x) Первая производная линейной функции – константа!
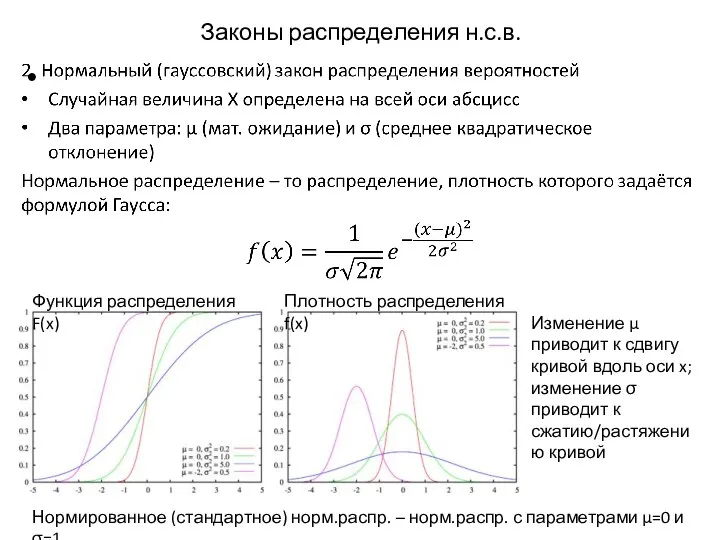
- 13. Законы распределения н.с.в. Функция распределения F(x) Плотность распределения f(x) Изменение μ приводит к сдвигу кривой вдоль
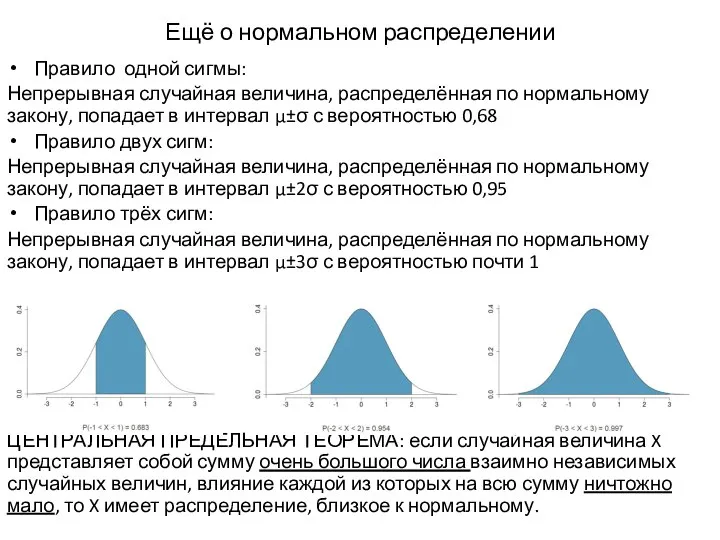
- 14. Ещё о нормальном распределении Правило одной сигмы: Непрерывная случайная величина, распределённая по нормальному закону, попадает в
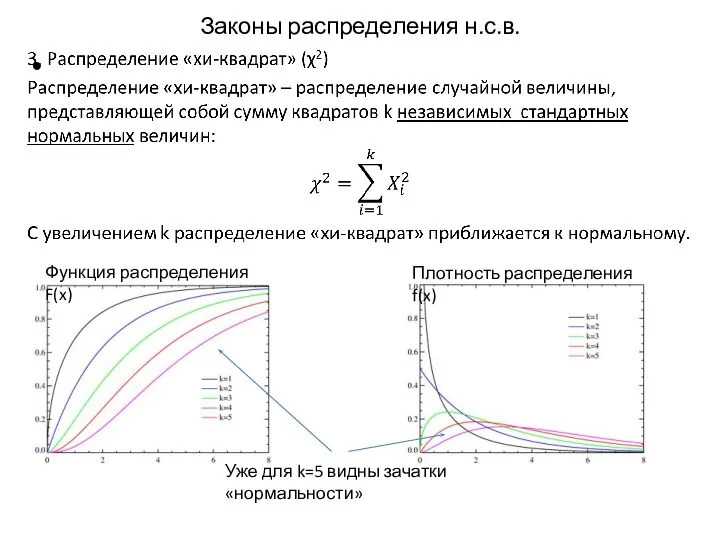
- 15. Законы распределения н.с.в. Функция распределения F(x) Плотность распределения f(x) Уже для k=5 видны зачатки «нормальности»
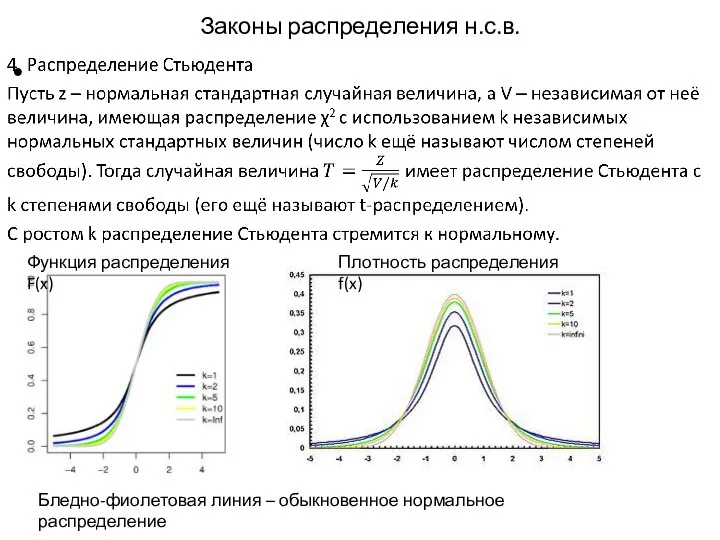
- 16. Законы распределения н.с.в. Функция распределения F(x) Плотность распределения f(x) Бледно-фиолетовая линия – обыкновенное нормальное распределение
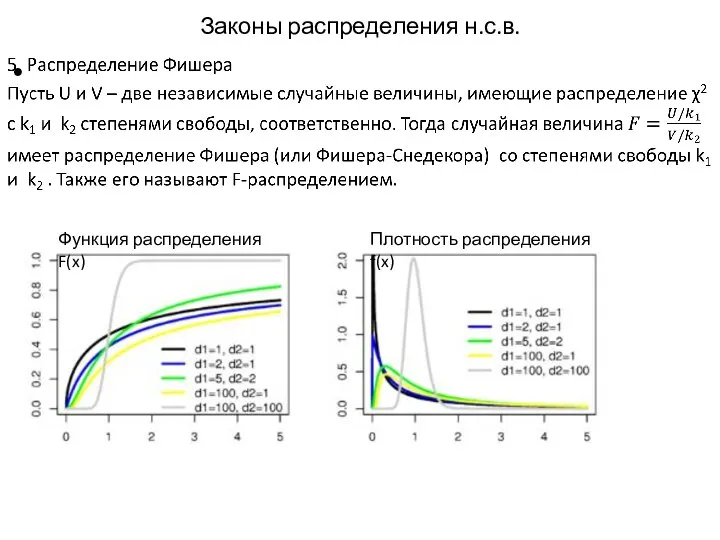
- 17. Законы распределения н.с.в. Функция распределения F(x) Плотность распределения f(x)
- 19. Скачать презентацию








 Урок с применением ИКТ Они были первыми
Урок с применением ИКТ Они были первыми Венегрет. Урок
Венегрет. Урок Построение сечений
Построение сечений Сумма углов треугольника
Сумма углов треугольника Интерактивный тренажёр Счет в пределах 15
Интерактивный тренажёр Счет в пределах 15 Функция у=х2 и ее график
Функция у=х2 и ее график Бинарные отношения
Бинарные отношения Геометрический смысл производной
Геометрический смысл производной Проценты. Основные задачи на проценты
Проценты. Основные задачи на проценты Теоретико-множественные преобразования
Теоретико-множественные преобразования Практикум по теме х2 = а
Практикум по теме х2 = а Самостоятельная работа. Задания
Самостоятельная работа. Задания Алгебра. Математичексая разминка
Алгебра. Математичексая разминка Поиск сокровищ. Изучений геометрических фигур
Поиск сокровищ. Изучений геометрических фигур Задачи на перебор вариантов
Задачи на перебор вариантов Презентация на тему ЛОГАРИФМЫ И ИХ СВОЙСТВА
Презентация на тему ЛОГАРИФМЫ И ИХ СВОЙСТВА  Сумма и разность синусов, косинусов
Сумма и разность синусов, косинусов Повторим… Уравнение линии на плоскости
Повторим… Уравнение линии на плоскости Деление дробей. Путешествие в Китай. 5 класс
Деление дробей. Путешествие в Китай. 5 класс Факториал
Факториал Презентация на тему Таблица умножения на 2 и 3
Презентация на тему Таблица умножения на 2 и 3  Тела вращения
Тела вращения Четные и нечетные числа
Четные и нечетные числа Кейс №2. Формализованные методы прогнозирования
Кейс №2. Формализованные методы прогнозирования Построение треугольника. 5 класс
Построение треугольника. 5 класс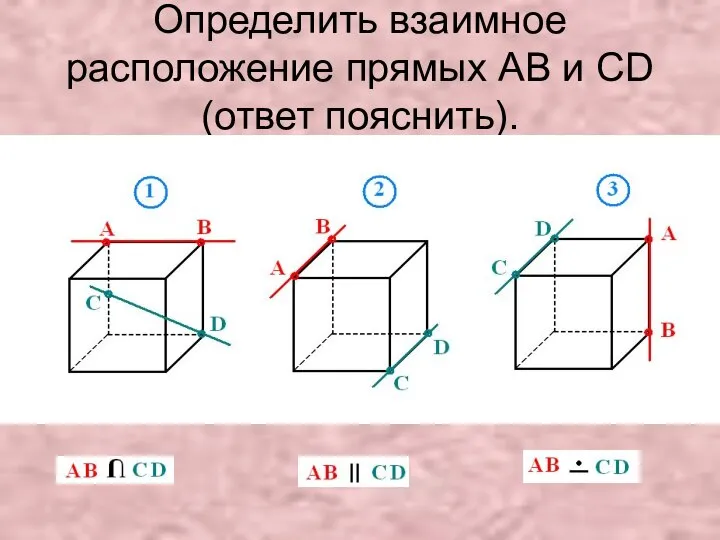 Прямая и плоскость в пространстве
Прямая и плоскость в пространстве Математические задачи для детей
Математические задачи для детей 3.7. Непрерывность функции
3.7. Непрерывность функции