Содержание
- 2. Теоретическая самостоятельная работа Проверка
- 3. Теоретическая самостоятельная работа
- 4. Проверочный тест Проверка
- 5. Ответы к тесту I вариант 1 – в), 2 – г), 3 – б). II вариант
- 6. Осевая и центральная симметрии
- 7. «Симметрия является той идеей, с помощью которой человек веками пытается объяснить и создать порядок, красоту и
- 8. В древности слово «СИММЕТРИЯ» употреблялось в значении «гармония», «красота». В переводе с греческого это слово означает
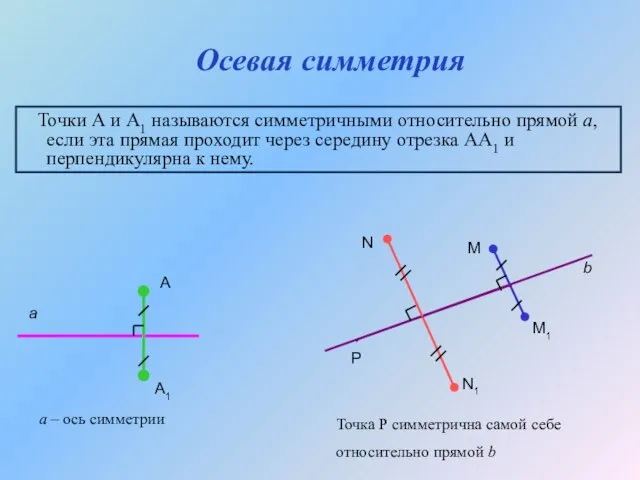
- 9. Осевая симметрия Точки А и А1 называются симметричными относительно прямой а, если эта прямая проходит через
- 10. Симметричность относительно прямой
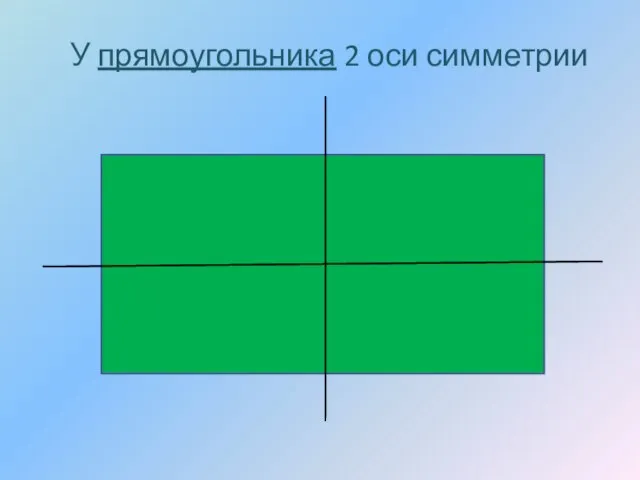
- 11. У прямоугольника 2 оси симметрии
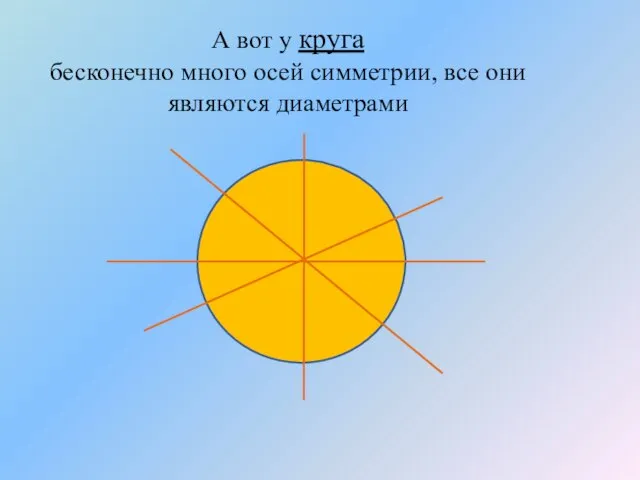
- 12. А вот у круга бесконечно много осей симметрии, все они являются диаметрами
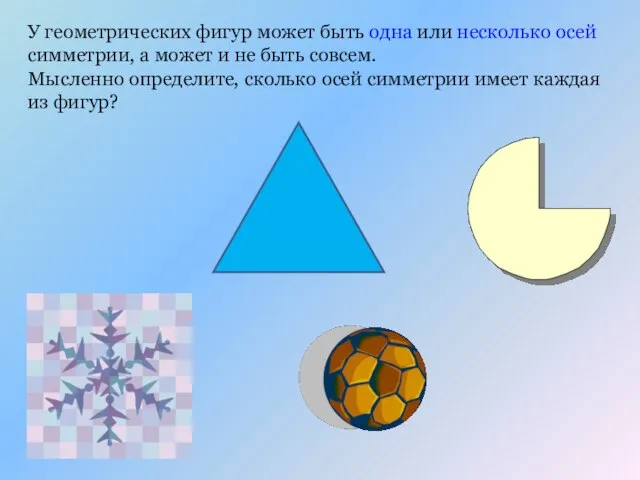
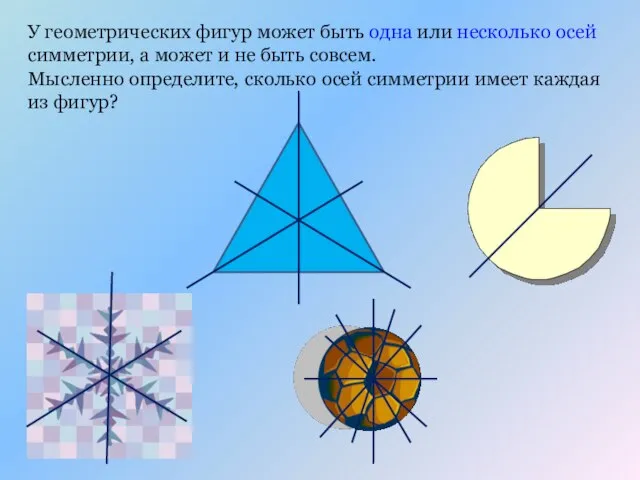
- 13. У геометрических фигур может быть одна или несколько осей симметрии, а может и не быть совсем.
- 14. У геометрических фигур может быть одна или несколько осей симметрии, а может и не быть совсем.
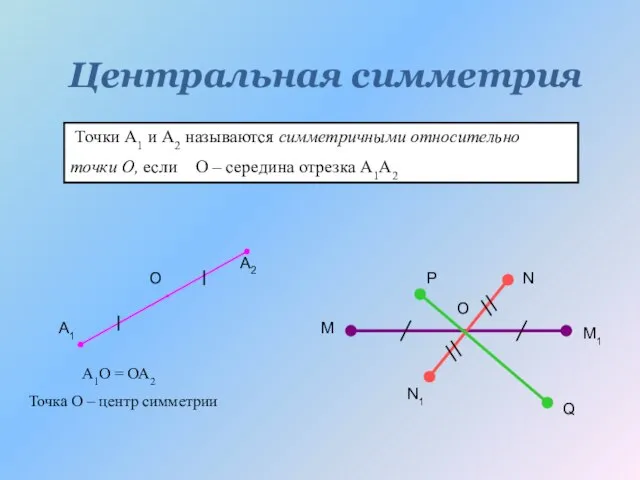
- 15. Центральная симметрия Точки А1 и А2 называются симметричными относительно точки О, если О – середина отрезка
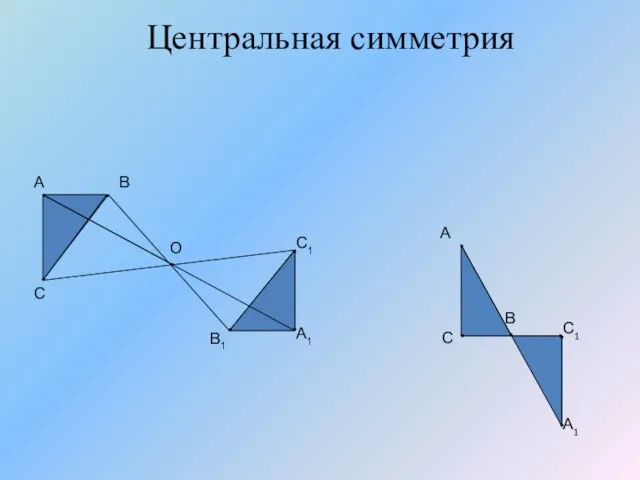
- 16. Центральная симметрия А В С А1 С1 А В С О С1 А1 В1
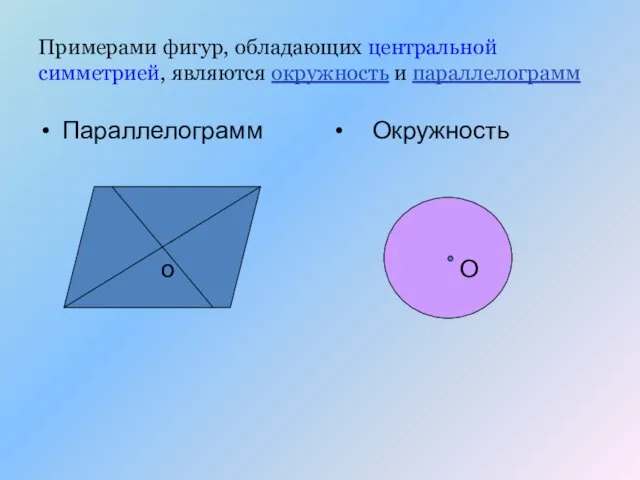
- 17. Примерами фигур, обладающих центральной симметрией, являются окружность и параллелограмм Параллелограмм Окружность о О
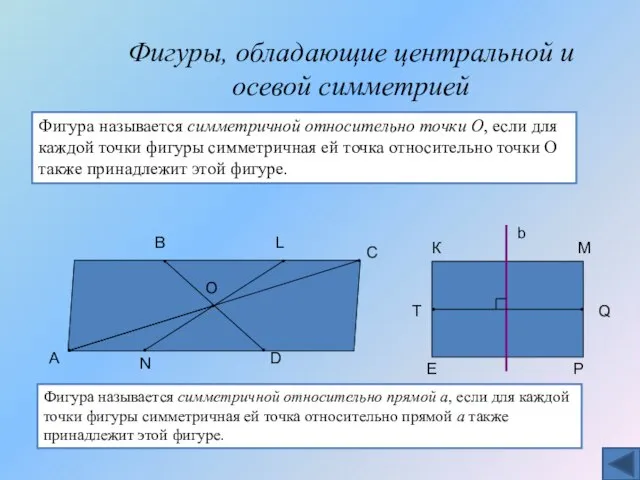
- 18. Фигуры, обладающие центральной и осевой симметрией О В А L N D С Фигура называется симметричной
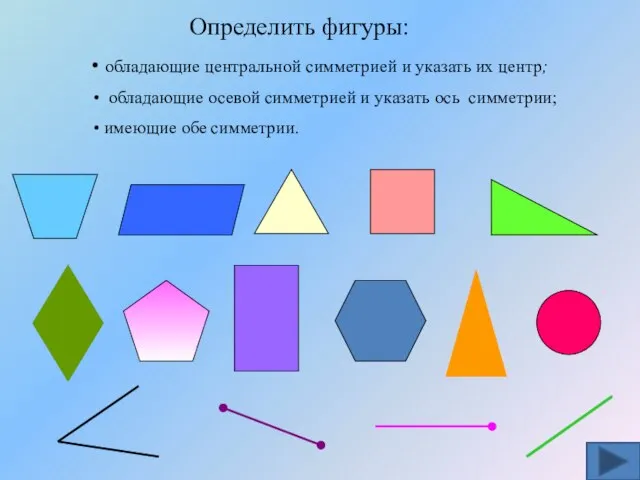
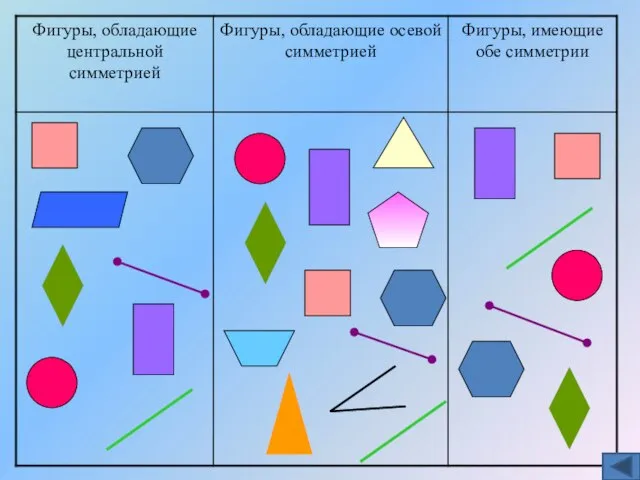
- 19. Определить фигуры: обладающие центральной симметрией и указать их центр; обладающие осевой симметрией и указать ось симметрии;
- 27. Буквы, имеющие горизонтальную ось симметрии В Е Ж З К Н О С Ф Х Э
- 28. Буквы, имеющие вертикальную ось симметрии А Д Ж Л М Н О П Т Ф Х
- 29. Буквы, не имеющие ось симметрии Б Г И Р У Ц Ч Я Щ
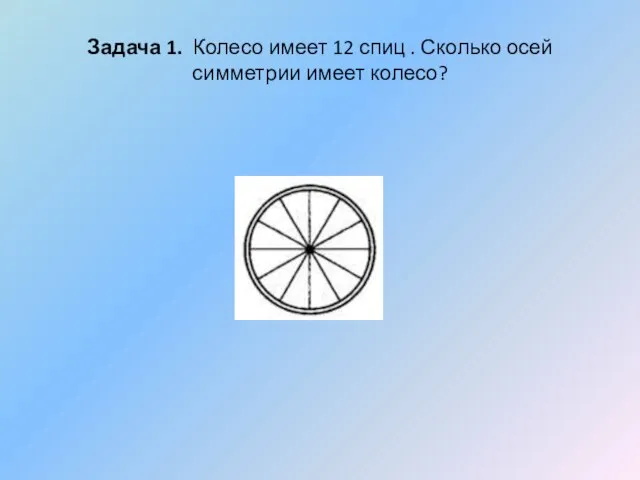
- 30. Задача 1. Колесо имеет 12 спиц . Сколько осей симметрии имеет колесо?
- 31. Сколько всего осей симметрии имеет фрагмент, изображённый на рисунке?
- 32. Сколько всего осей симметрии имеет фрагмент, изображённый на рисунке?
- 34. Скачать презентацию



















 قدرمطلقی درجه اول
قدرمطلقی درجه اول Способы решения показательных уравнений
Способы решения показательных уравнений Преобразования графиков
Преобразования графиков Математика. 3 класс
Математика. 3 класс Презентация на тему Страна отрицательных чисел
Презентация на тему Страна отрицательных чисел  Презентация на тему Угол вписанный в окружность
Презентация на тему Угол вписанный в окружность  Великолепная пятерка. Математический калейдоскоп
Великолепная пятерка. Математический калейдоскоп Обобщающий урок по начертательной геометрии прямая. Плоскость
Обобщающий урок по начертательной геометрии прямая. Плоскость Раскрытие скобок
Раскрытие скобок Планиметрия. Четырёхугольники
Планиметрия. Четырёхугольники Решение по готовы чертежам по теме: Длина окружности, 9 класс
Решение по готовы чертежам по теме: Длина окружности, 9 класс Сложение и вычитание дробей с разными знаменателями
Сложение и вычитание дробей с разными знаменателями Матричный способ решения СЛАУ и метод Крамера
Матричный способ решения СЛАУ и метод Крамера Рациональные приемы вычислений
Рациональные приемы вычислений Подготовка к ВПР. Равенство
Подготовка к ВПР. Равенство pril1
pril1 Шкала. Координатный луч
Шкала. Координатный луч Степенные ряды
Степенные ряды Числовые промежутки
Числовые промежутки Prezentado de enspezoj
Prezentado de enspezoj Сравнение чисел. 1 класс
Сравнение чисел. 1 класс Раскрытие скобок
Раскрытие скобок Математика 1 класс. УМК Перспектива. Урок 1. Форма предметов
Математика 1 класс. УМК Перспектива. Урок 1. Форма предметов Построение информационной модели метода изготовления изделия
Построение информационной модели метода изготовления изделия Геометрические построения
Геометрические построения Числовая окружность на координатной плоскости
Числовая окружность на координатной плоскости ЕГЭ 2021. Задания 1-19 (11 класс)
ЕГЭ 2021. Задания 1-19 (11 класс) Метрология
Метрология