Основные законы распределения непрерывных случайных величин

Непрерывная СВ
НСВ называется такая величина, возможные значения которой непрерывно заполняют некоторый интервал (конечный или бесконечный).
Число всех возможных значений НСВ бесконечно.
Пример: Случайное отклонение по дальности точки падения снаряда от цели.

Функция распределения НСВ
Функцией распределения называют F(x), определяющую для каждого значения x вероятность того, что СВХ примет значение, меньшее х, т.е. согласно определению
F(x)=P(X
F(x) определяет и ДСВ и НСВ. F(x) также называют интегральной функцией распределения.

Функция распределения НСВ
Свойства функции распределения:
если
, то
следствие:
Если все возможные значения x СВХ принадлежат интервалу (a;b), то при a<=a F(x)=0, а при x>=b F(x)=1
Следствие:
1.
2.
3.
Функция распределения непрерывна слева

Функция плотности распределения НСВ
Функцией плотности распределения вероятностей называют первую производную от функции F(x), то есть f(x)=F`(x). f(x) называют дифференциальной функцией. Вероятность того, что НСВХ примет значения, принадлежащие интервалу (a;b) вычисляемые по формуле
Зная плотность распределения, можно найти функцию распределения
Свойства:
, в частности, если все возможные значения СВ принадлежат (a;b), то
1.
2.

Числовые хар-ки НСВ
Математическое ожидание НСВХ, все возможные значения которой принадлежат интервалу (a;b), определяется равенством:
Дисперсия НСВХ, все возможные значения которой принадлежат интервалу (a;b), определяется равенством:
При решении задач применима формула:

Числовые хар-ки НСВ
Среднеквадратичное отклонение определяется так же, как и для ДСВ:
Начальный момент k-ого порядка НСВ определяется равенством:

Числовые хар-ки НСВ
Центральный момент k-ого порядка НСВХ, все возможные значения которой принадлежат интервалу (a:b), определяется равенством:

Числовые хар-ки НСВ
Если все возможные значения НСВХ принадлежат всей числовой оси ОХ, то во всех вышеуказанных формулах определенный интеграл заменяется несобственным интегралом с бесконечными нижним и верхним пределами

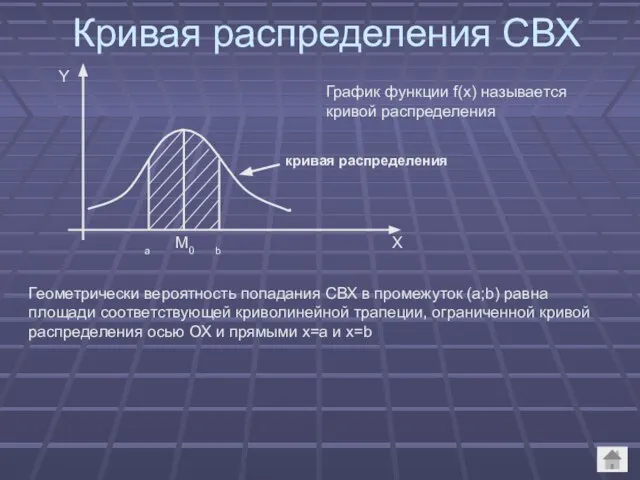
Кривая распределения СВХ
График функции f(x) называется кривой распределения
кривая распределения
Геометрически вероятность попадания СВХ в промежуток (a;b) равна площади соответствующей криволинейной трапеции, ограниченной кривой распределения осью ОХ и прямыми x=a и x=b

Мода
Модой ДСВХ называется ее наиболее вероятное значение. Модой НСВХ называется такое ее значение M0, при котором плотность распределения максимальная.
Для нахождения моды НСВ необходимо найти максимум функции с помощью первой или второй производной.
M0=2, т.к. 0.1<0.6>0.3
Геометрически мода является абсциссой той точки кривой или полигона распределения, ордината которой максимальна

Медиана
Медианой НСВХ называется такое ее значение Ме, для которого одинаково вероятно, окажется ли случайная величина больше или меньше Ме, т.е. P(x< Ме)=P(x> Ме)=0.5
Ордината, проведенная к точке с абсциссой, равной Ме, делит пополам площадь, ограниченную кривой или полигоном распределения. Если прямая x=a является осью симметрии кривой распределения y=f(x), то М0=Ме=М(Х)=a

Равномерное распределение плотности
Равномерным называется распределение таких СВ, все значения которых лежат на некотором отрезке (a;b) и имеют постоянную плотность вероятности на этом отрезке
Математическое ожидание, дисперсия, среднеквадратичное отклонение равномерно распределенной СВ:

Показательное распределение