определения функции, в которых производная обращается в нуль или не существует.
если в некоторой точке х0 производная функции f ( х) обращается в нуль и, кроме того, проходя через нее слева направо, меняет свой знак, то в этой точке функция достигает экстремума:
если производная меняет знак с «+» на «–», то х0– точка максимума функции f (х ) ;
- если производная меняет знак с «–» на «+», то х0 – точка минимума функции f (х ).
Необходимое условие экстремума
(теорема Ферма): если точка х0 является точкой экстремума функции f (х), и в этой точке существует производная f ’(x), то она равна нулю: f ’(x) =0 .
![Функция f(x) называется возрастающей на отрезке [a; b] если для любых двух](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/860541/slide-1.jpg)


 Арифметика в позиционных системах счисления
Арифметика в позиционных системах счисления Презентация на тему Методы решения уравнений высших степеней
Презентация на тему Методы решения уравнений высших степеней  Формула Бернулли и ее следствия. Вероятностные модели реальных явлений и процессов
Формула Бернулли и ее следствия. Вероятностные модели реальных явлений и процессов Тайна Ворона Метра, или Сказка об удивительных приключениях – превращениях Квадрата
Тайна Ворона Метра, или Сказка об удивительных приключениях – превращениях Квадрата На оптимизацию с решением
На оптимизацию с решением Иллюзии и математические парадоксы
Иллюзии и математические парадоксы Двугранные углы
Двугранные углы Множества
Множества Предел функции
Предел функции Презентация на тему Квадратные корни. Арифметический квадратный корень
Презентация на тему Квадратные корни. Арифметический квадратный корень 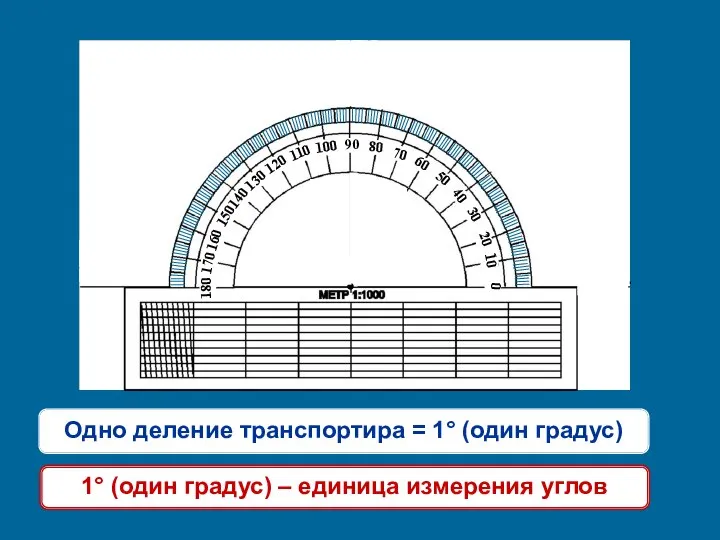 Измерение углов, транспортир
Измерение углов, транспортир Подготовка к ЕГЭ. Повторение. Математика
Подготовка к ЕГЭ. Повторение. Математика Средняя линия треугольника
Средняя линия треугольника Функции одной переменной (лекция № 1)
Функции одной переменной (лекция № 1) Элементы высшей математики
Элементы высшей математики Вредная задача
Вредная задача Презентация на тему Комбинаторные задачи: перестановки
Презентация на тему Комбинаторные задачи: перестановки  Обыкновенные дифференциальные уравнения. Вариант 4
Обыкновенные дифференциальные уравнения. Вариант 4 Предел функции в точке и на бесконечности
Предел функции в точке и на бесконечности Практическая работа
Практическая работа Простейшие уравнения
Простейшие уравнения Математика
Математика Свойства тригонометрических функций и их графики
Свойства тригонометрических функций и их графики Вентильные схемы и алгебра логики
Вентильные схемы и алгебра логики Произведение дробей, обратных друг другу
Произведение дробей, обратных друг другу Задания Незнайки
Задания Незнайки Какому числу равен квадрат числа 11
Какому числу равен квадрат числа 11 Занимательные задачи (4 класс)
Занимательные задачи (4 класс)