Содержание
- 2. Источники Аляев Ю. А., Тюрин С. Ф. Дискретная математика и математическая логика. Андерсон Дж. Дискретная математика
- 3. Отображение (функция)
- 4. Инъекция, сюръекция, биекция
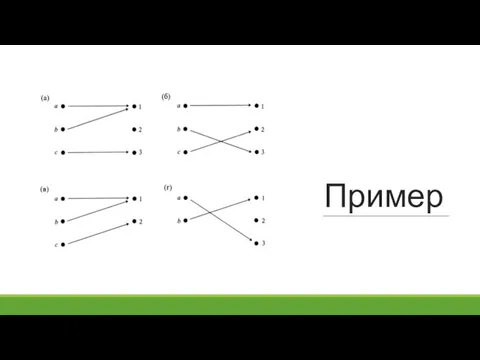
- 5. Пример
- 6. Обратная функция
- 7. Композиция функций
- 8. Бесконечные множества
- 9. Конечные и бесконечные множества КОНЕЧНОЕ МНОЖЕСТВО БЕСКОНЕЧНОЕ МНОЖЕСТВО Множество, не являющееся конечным. Множество, мощность которого не
- 10. Равномощность множеств
- 11. Бесконечные множества СЧЁТНОЕ МНОЖЕСТВО Бесконечное множество, элементы которого возможно пронумеровать натуральными числами. Множество, для которого можно
- 12. Мощность множества Класс эквивалентности по отношению равномощности.
- 13. Источники Аляев Ю. А., Тюрин С. Ф. Дискретная математика и математическая логика. Андерсон Дж. Дискретная математика
- 14. Специальные функции
- 15. Бинарная операция
- 16. Универсальная алгебра
- 17. Полугруппа
- 18. Группа
- 19. Пример 1
- 20. Пример 2
- 21. Пример 3
- 22. Пример 4
- 23. Пример 5
- 24. Операции коммутативной группы АДДИТИВНАЯ МУЛЬТИПЛИКАТИВНАЯ Обозначение операции: Нейтральный элемент: Противоположный элемент:
- 25. Кольцо
- 26. Пример 1
- 27. Поле Если кольцо имеет мультипликативный нейтральный элемент (единицу), оно называется кольцом с единицей. Если операция умножения
- 29. Скачать презентацию

























 Комплексные числа и координатная плоскость. Решение примеров на построение комплексных чисел на комплексной плоскости
Комплексные числа и координатная плоскость. Решение примеров на построение комплексных чисел на комплексной плоскости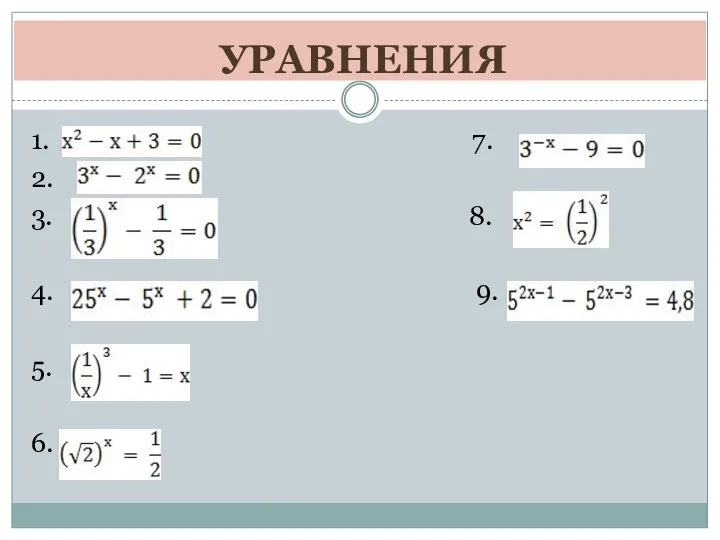 Решение показателей уравнений
Решение показателей уравнений Римские числа
Римские числа Повторительно-обобщающий урок по теме: Показательная функция. 11 класс
Повторительно-обобщающий урок по теме: Показательная функция. 11 класс Теоремы о пределах. Нахождение пределов
Теоремы о пределах. Нахождение пределов Презентация на тему Средняя линия треугольника
Презентация на тему Средняя линия треугольника  Реши примеры устно. 2 класс
Реши примеры устно. 2 класс Декартова система координат
Декартова система координат Презентация на тему Математический КВН
Презентация на тему Математический КВН  Диалектика как методология научного познания
Диалектика как методология научного познания Экологические понятия в математике
Экологические понятия в математике Треугольники. Геометрия, 7 класс
Треугольники. Геометрия, 7 класс ПРИЗНАКИ ПАРАЛЛЕЛОГРАММА
ПРИЗНАКИ ПАРАЛЛЕЛОГРАММА Параллельные прямые. 7 класс
Параллельные прямые. 7 класс Научные открытия России. Задача тысячелетия. Теорема Пуанкаре
Научные открытия России. Задача тысячелетия. Теорема Пуанкаре Дифференциальные уравнения и их применение в медицине
Дифференциальные уравнения и их применение в медицине Динамика системы вблизи цикла
Динамика системы вблизи цикла Деление с остатком
Деление с остатком Парная линейная регрессия
Парная линейная регрессия Компоненти дій
Компоненти дій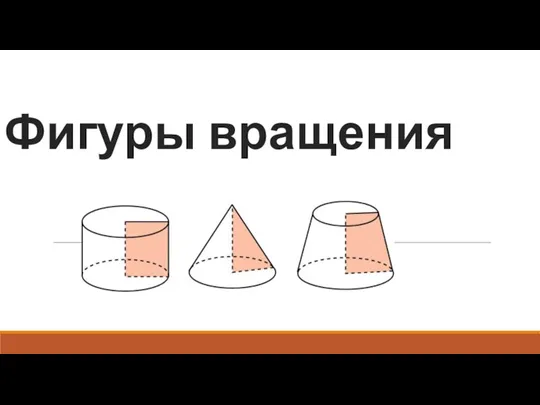 Фигуры вращения
Фигуры вращения Элементы комбинаторики. Решение простейших комбинаторных задач
Элементы комбинаторики. Решение простейших комбинаторных задач Таблица умножения с 7 до 9
Таблица умножения с 7 до 9 Производная и первообразная
Производная и первообразная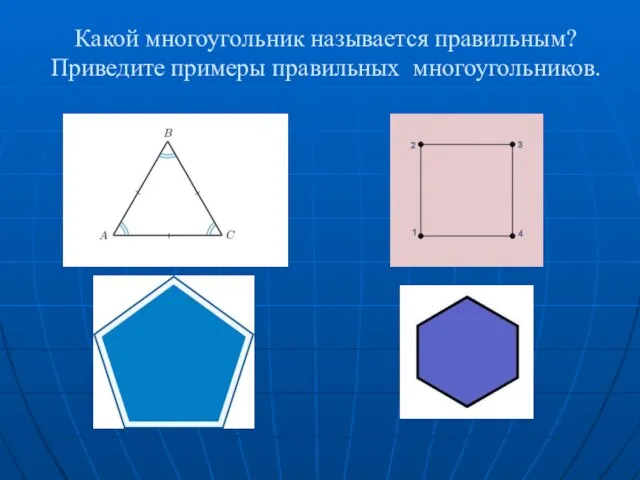 Какой многоугольник называется правильным? Приведите примеры правильных многоугольников
Какой многоугольник называется правильным? Приведите примеры правильных многоугольников Занимательные задачи
Занимательные задачи Основное свойство дроби
Основное свойство дроби