Слайд 2Формула Ньютона-Лейбница:
Не существование первообразной:

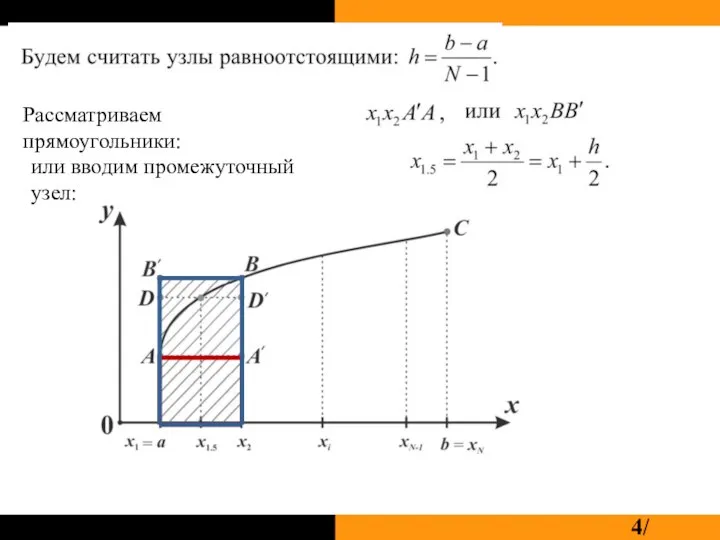
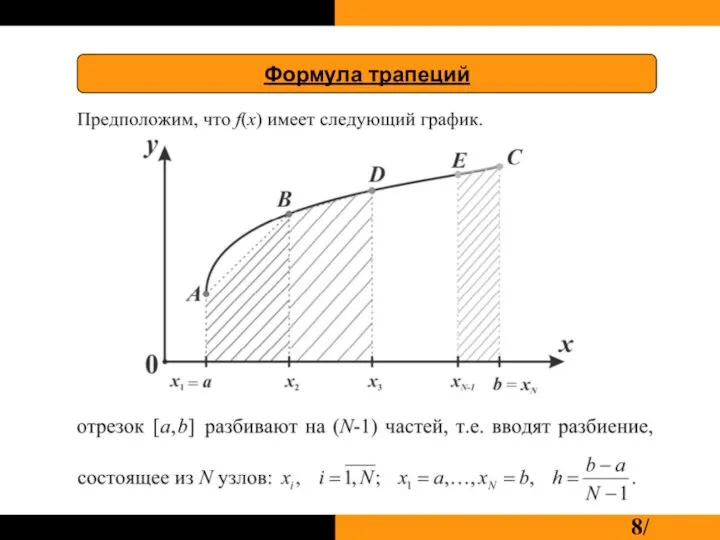
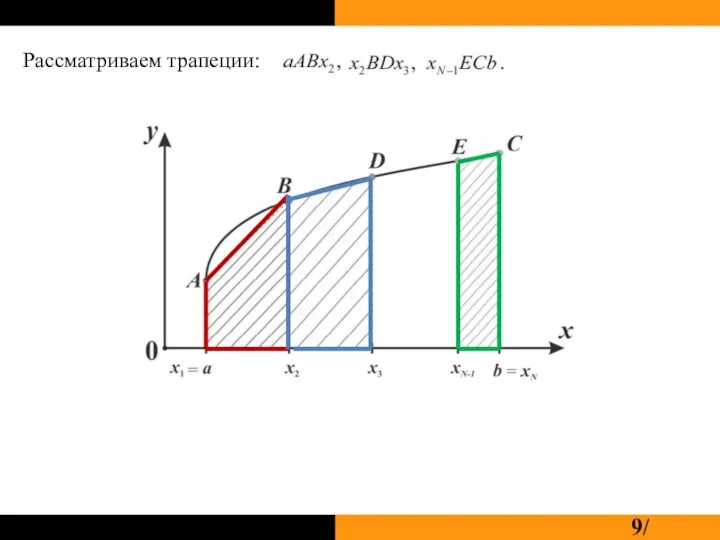
Слайд 4Рассматриваем прямоугольники:
или вводим промежуточный узел:
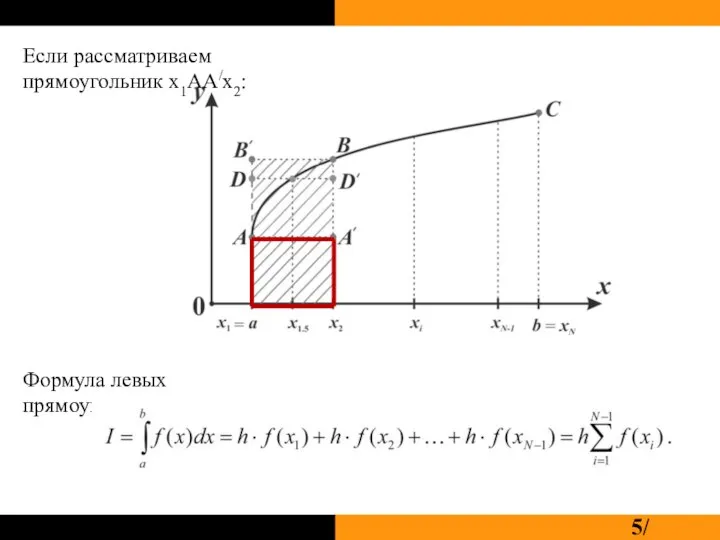
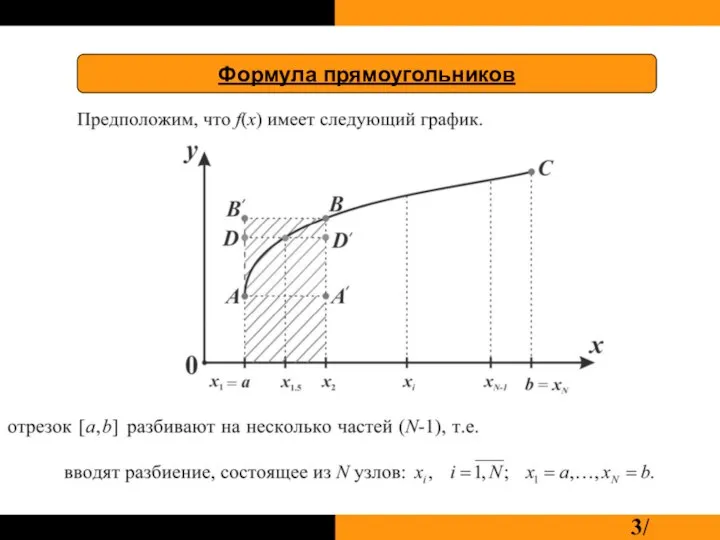
Слайд 5Если рассматриваем прямоугольник x1AA/x2:
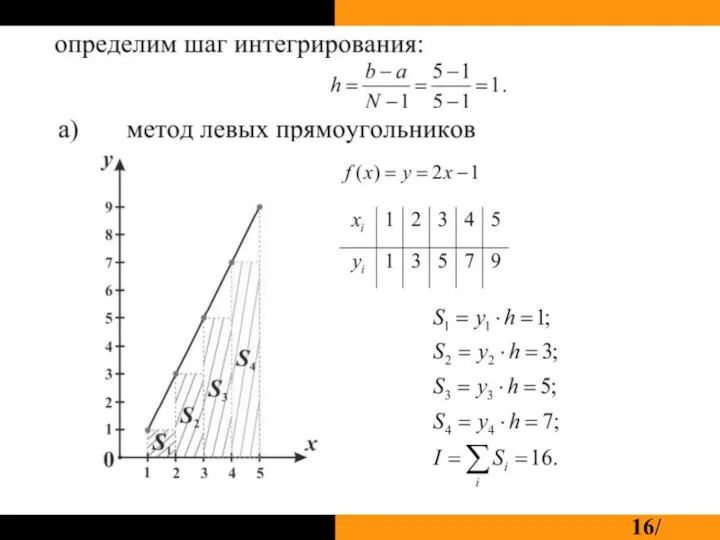
Формула левых прямоугольников:
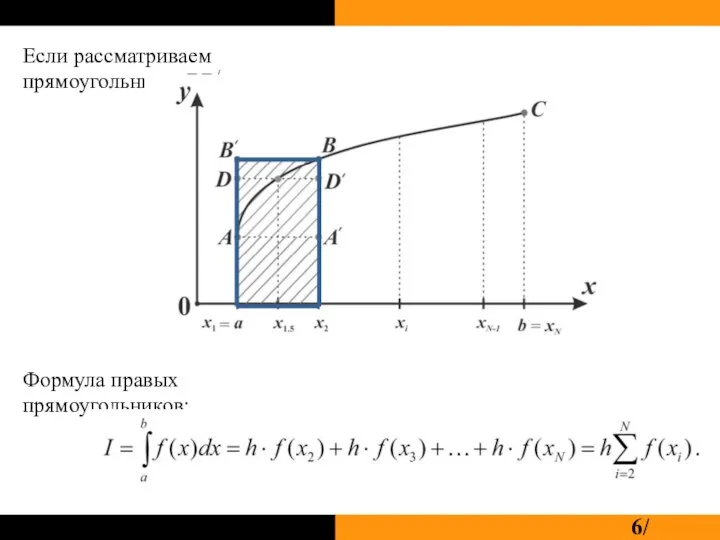
Слайд 6Если рассматриваем прямоугольник x1ВВ/x2:
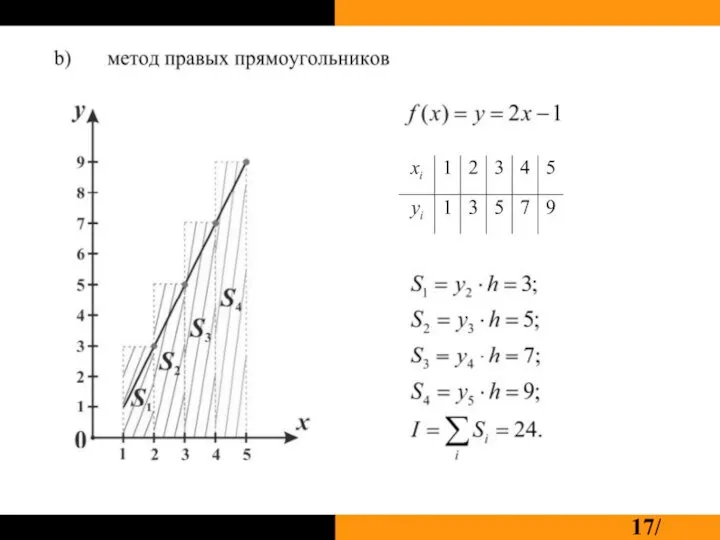
Формула правых прямоугольников:
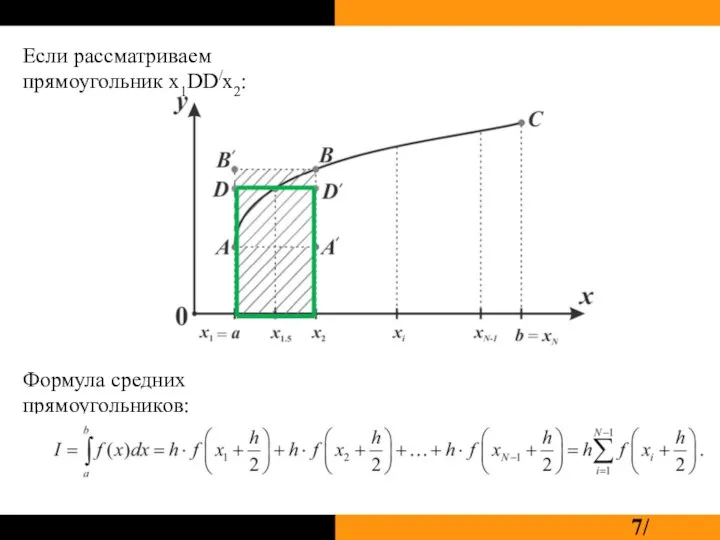
Слайд 7Если рассматриваем прямоугольник x1DD/x2:
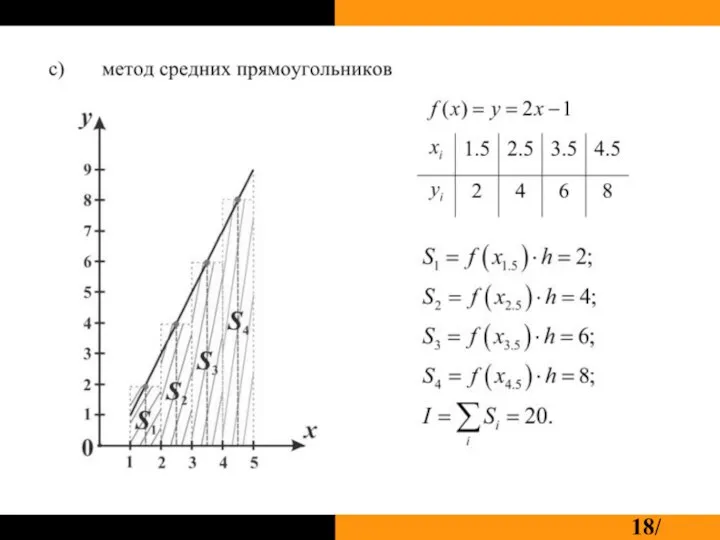
Формула средних прямоугольников:
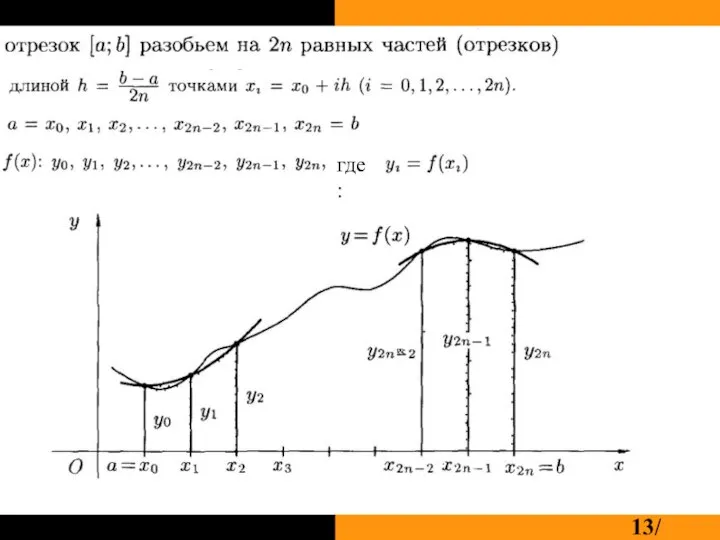
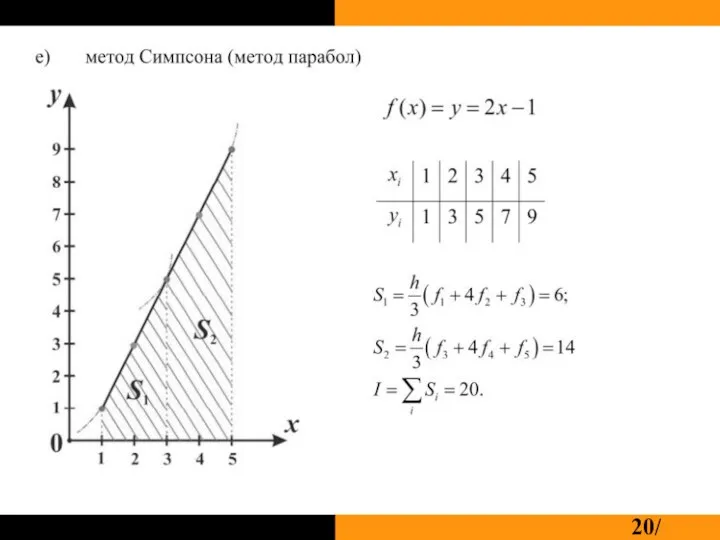
Слайд 11Формула Симпсона(метод парабол):
Найдем площадь криволинейной трапеции, ограниченной сверху
графиком параболы:
сбоку прямыми:

Слайд 15Примеры вычисления определенного интеграла:

Слайд 27Коэффициенты многочлена должны удовлетворять условию:
Данный подход малоэффективен

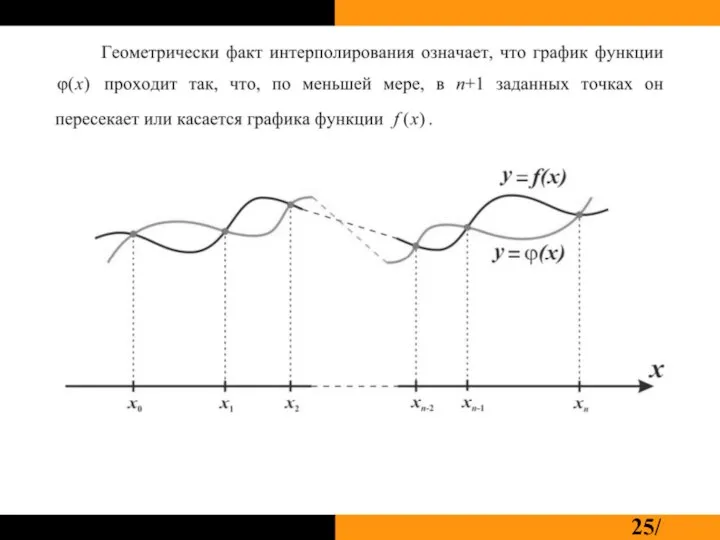
Слайд 32Многочлен Лагранжа записывается с помощью двух базисных
Многочленов первой степени :






















 Логарифмическая линейка
Логарифмическая линейка Простые задачи на умножение и деление
Простые задачи на умножение и деление Теорема о трёх перпендикулярах
Теорема о трёх перпендикулярах Методы эвристических приемов
Методы эвристических приемов Применение аксиом и их следствий
Применение аксиом и их следствий Математическое описание случайных явлений
Математическое описание случайных явлений Четырёхугольники. Урок-зачет
Четырёхугольники. Урок-зачет Таблица сложения
Таблица сложения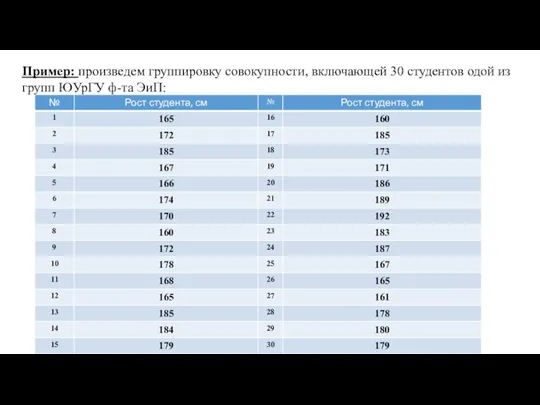 Группировка
Группировка Тренажер Состав числа
Тренажер Состав числа Экстремум функции. Признак постоянства функции. Исследование на экстремум
Экстремум функции. Признак постоянства функции. Исследование на экстремум Логические операции. Конъюнкция, дизъюнкция, отрицание, импликация, эквивалентность
Логические операции. Конъюнкция, дизъюнкция, отрицание, импликация, эквивалентность Пропорции. Проценты. Диаграммы
Пропорции. Проценты. Диаграммы Гра в нормальній формі. Формалізований вид гри
Гра в нормальній формі. Формалізований вид гри Сокращение дробей. Графический диктант
Сокращение дробей. Графический диктант Без слов и грамматики не учат математике
Без слов и грамматики не учат математике Сложение смешанных дробей
Сложение смешанных дробей Статистические характеристики. Среднее арифметическое, мода, медиана называются средними результатами измерений
Статистические характеристики. Среднее арифметическое, мода, медиана называются средними результатами измерений Презентация на тему Математическая сказка "Гуси лебеди" 3 класс
Презентация на тему Математическая сказка "Гуси лебеди" 3 класс  Теория вероятностей и математическая статистика. Многомерные распределения вероятностей
Теория вероятностей и математическая статистика. Многомерные распределения вероятностей Математика для дошкольников (средняя группа)
Математика для дошкольников (средняя группа) Преобразование выражения Asinx+Bcosx к виду Csin(x+t)
Преобразование выражения Asinx+Bcosx к виду Csin(x+t) Координаты вектора
Координаты вектора Готовимся к ОГЭ по математике
Готовимся к ОГЭ по математике Эллипс
Эллипс Сокращение дробей
Сокращение дробей Параллельность в пространстве. Решение задач
Параллельность в пространстве. Решение задач Понятие вектора. Равенство векторов
Понятие вектора. Равенство векторов