Слайд 32. Постановка задачи (продолжение)

Слайд 43. Постановка задачи (продолжение)

Слайд 54. Постановка задачи (продолжение)
Что-то сказать про это

Слайд 65. Метод сближающихся многогранников

Слайд 76. Метод сближающихся многогранников (продолжение)

Слайд 87. Сеточный метод
Идея метода:
вписать окружность
построить на окружности сетку
из

центра окружности, через точку сетки провести прямую до пересечения с аппроксимируемым телом
полученная точка - вершиной для внутреннего многогранника и точка касания для внешнего
Слайд 98. Сеточный метод(продолжение)
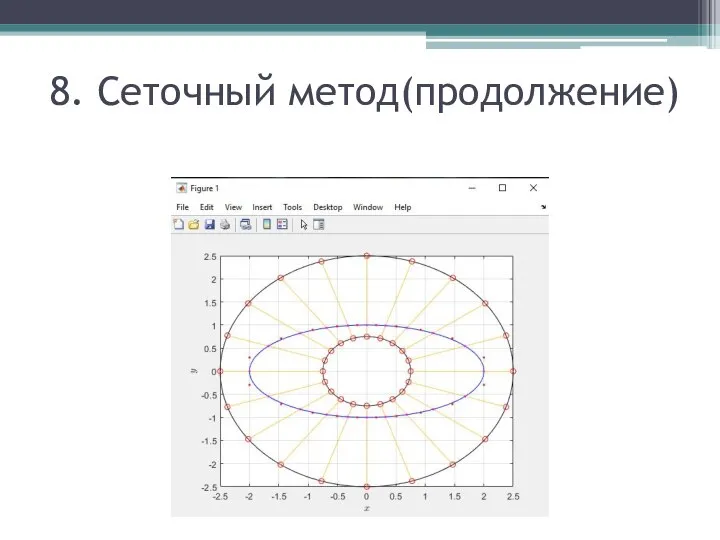
Слайд 10
Размерность: 2
Матрица системы А:
0.100000 -0.200000
0.400000 0.300000
Координаты точки x:
10.000000 10.000000
Значения величин полуосей:
a: 1.000000
b: 2.000000
Координаты X, Y

(Z) центра эллипса:
X: 0.000000
Y: 0.000000
Количество начальных точек на многограннике Р: 3
Начальные точки многогранника Р:
0.997645 -0.137192
-0.439416 1.796567
-0.558228 -1.659375
Начальные точки многогранника Q:
1.116456 3.318750
-1.995289 0.274384
0.878833 -3.593134
Слайд 11Множества 0-упрпавляемости в методе СМ

Слайд 12Множества 0-упрпавляемости в сеточном методе
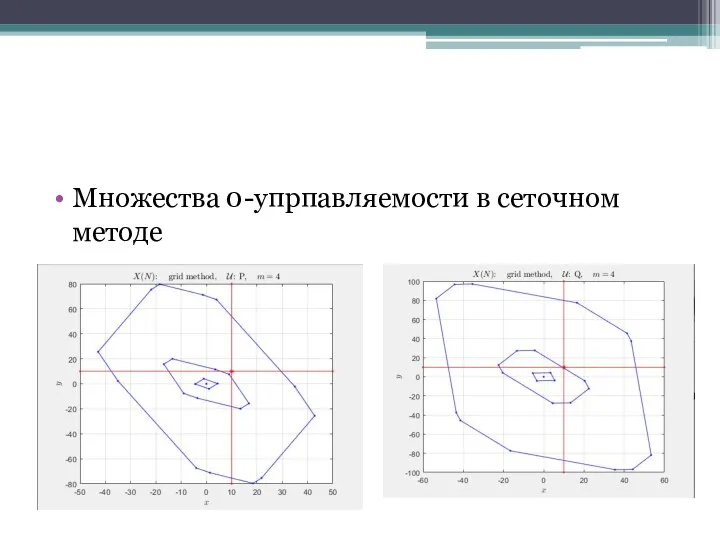
Слайд 13-- Полиэдральная аппроксимация --
Оценки NPmin и NQmin для текущего значения m точек

многогранника Р:
m | NPmin | NQmin
-------------------------
3 3 2
4 3 2
5 3 2
6 3 3
Оценка Nmin полиэдральным методом: 3
Потребовалось точек множества U: 6
-- Сеточная аппроксимация --
Оценки NPmin и NQmin для текущего значения m точек многогранника Р:
m | NPmin | NQmin
--------------------------
3 3 2
4 3 3
Оценка Nmin сеточным методом: 3
Потребовалось точек множества U: 4
Слайд 14
Размерность: 2
Матрица системы А:
0.100000 -0.200000
0.400000 0.300000
Координаты точки p:
-35.000000 56.000000
Значения величин полуосей:
a: 1.000000
b: 2.000000
Координаты X, Y

(Z) центра элипса:
X: 0.000000
Y: 0.000000
Количество начальных точек на многограннике Р: 3
Начальные точки многогранника Р:
-0.108651 1.988160
-0.806573 -1.182269
0.915224 -0.805891
Начальные точки многогранника Q:
-1.830448 1.611781
0.217302 -3.976320
1.613146 2.364539
Слайд 15Множества 0-упрпавляемости в методе СМ
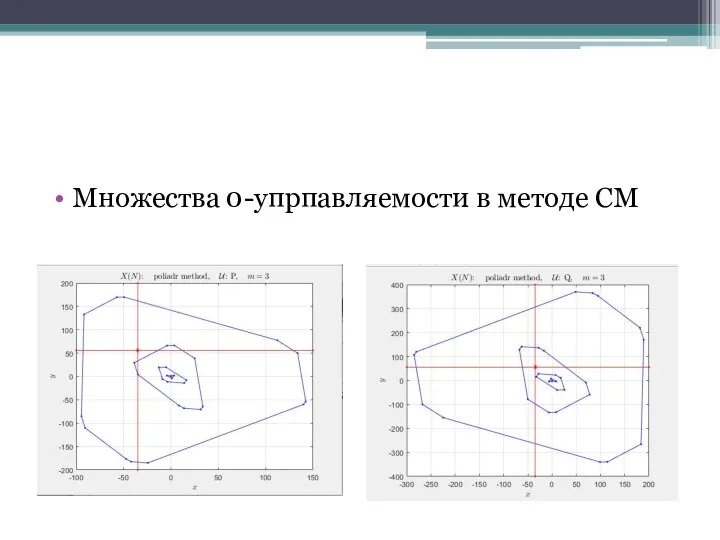
Слайд 16Множества 0-упрпавляемости в сеточном методе

Слайд 17-- Полиэдральная аппроксимация --
Оценки NPmin и NQmin для текущего значения m точек

многогранника Р:
m | NPmin | NQmin
-------------------------
3 4 4
Оценка Nmin полиэдральным методом: 4
Потребовалось точек множества U: 3
-- Сеточная аппроксимация --
Оценки NPmin и NQmin для текущего значения m точек многогранника Р:
m | NPmin | NQmin
-------------------------
3 4 4
Оценка Nmin сеточным методом: 4
Потребовалось точек множества U: 3
Слайд 18
Размерность: 2
Матрица системы А:
0.100000 -0.200000
0.400000 0.300000
Координаты точки p:
270.000000 -560.000000
Значения величин полуосей:
a: 1.000000
b: 2.000000
Координаты X, Y

(Z) центра элипса:
X: 0.000000
Y: 0.000000
Количество начальных точек на многограннике Р: 3
Начальные точки многогранника Р:
0.969545 0.489823
-0.696872 1.434391
-0.272673 -1.924213
Начальные точки многогранника Q:
0.545347 3.848427
-1.939091 -0.979645
1.393744 -2.868782
Слайд 19Множества 0-упрпавляемости в методе СМ
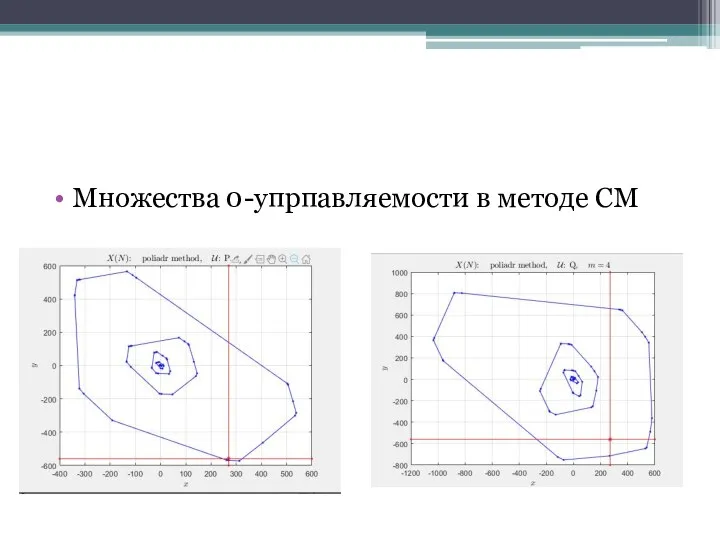
Слайд 20Множества 0-упрпавляемости в сеточном методе
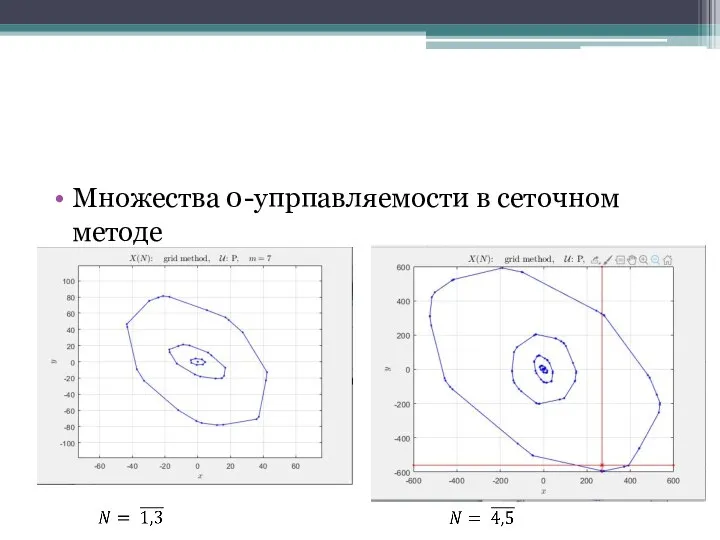
Слайд 21Множества 0-упрпавляемости в сеточном методе (продолжение)
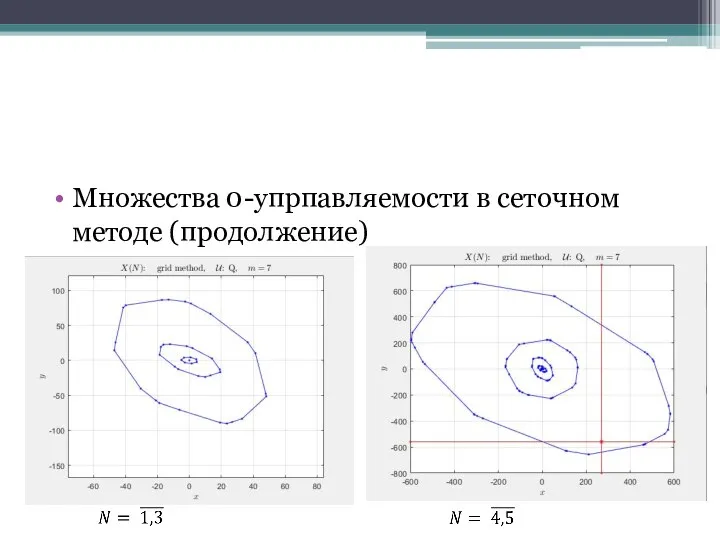
Слайд 22-- Полиэдральная аппроксимация --
Оценки NPmin и NQmin для текущего значения m точек

многогранника Р:
m | NPmin | NQmin
------------------------
3 6 5
4 5 5
Оценка Nmin полиэдральным методом: 5
Потребовалось точек множества U: 4
-- Сеточная аппроксимация --
Оценки NPmin и NQmin для текущего значения m точек многогранника Р:
m | NPmin | NQmin
-------------------------
3 6 5
4 6 5
5 6 5
6 6 5
7 5 5
Оценка Nmin сеточным методом: 5
Потребовалось точек множества U: 7





















 Пперпендикулярные прямые
Пперпендикулярные прямые Решение текстовых задач с помощью уравнений
Решение текстовых задач с помощью уравнений Логические операции
Логические операции Задачи на кратное сравнение
Задачи на кратное сравнение Связь суммы со слагаемыми
Связь суммы со слагаемыми Решение задач с помощью систем уравнений (часть 2)
Решение задач с помощью систем уравнений (часть 2) Сечение куба, призмы, пирамиды
Сечение куба, призмы, пирамиды Основные понятия и определения метрологии. Лекция 1
Основные понятия и определения метрологии. Лекция 1 Математическая викторина. 2 тур. Великие и знаменитые
Математическая викторина. 2 тур. Великие и знаменитые Сократите дробь решите систему, уравнение, упростите выражение и т.д
Сократите дробь решите систему, уравнение, упростите выражение и т.д Показательная функция и ее применение
Показательная функция и ее применение Таблицы. Алгебра 7 класс
Таблицы. Алгебра 7 класс Расстояние от точки до прямой. Решение задач
Расстояние от точки до прямой. Решение задач Перпендикуляр и наклонная
Перпендикуляр и наклонная Математическое моделирование
Математическое моделирование Арифметическая прогрессия. Всё в твоих руках
Арифметическая прогрессия. Всё в твоих руках ПРОЕКТ: Реализация требований ФГОС ООО при обучении учащихся 6 класса теме «Сложение и вычитание рациональных чисел»
ПРОЕКТ: Реализация требований ФГОС ООО при обучении учащихся 6 класса теме «Сложение и вычитание рациональных чисел» 3_Equations_2
3_Equations_2 Выражения с переменными
Выражения с переменными Перпендикулярные прямые в пространстве
Перпендикулярные прямые в пространстве Методика изучения геометрического материала
Методика изучения геометрического материала Соотношение числа и цифры. Считаем от 1 до 9
Соотношение числа и цифры. Считаем от 1 до 9 Задачи на нахождение неизвестного по двум разностям
Задачи на нахождение неизвестного по двум разностям Исторические задачи комбинаторики и теории вероятностей. Самостоятельная внеаудиторная работа 1
Исторические задачи комбинаторики и теории вероятностей. Самостоятельная внеаудиторная работа 1 Формулы тангенсов и котангенсов
Формулы тангенсов и котангенсов Уравнение древности. Франсуа Виет
Уравнение древности. Франсуа Виет Великолепная пятерка. Математический калейдоскоп
Великолепная пятерка. Математический калейдоскоп Умножение обыкновенных дробей
Умножение обыкновенных дробей